Три задачи по комбинаторике. КОМБИНАТОРИКА 3 задачи. Решение. Обозначим через Р
 Скачать 30.63 Kb.
|
|
№4. Сколько существует целых чисел в диапазоне от 0 до 100 000, содержащих ровно две цифры «8» и одну цифру «4»? Решение. Числа, содержащие ровно две цифры «8» и одну цифру «4», в диапазоне от 0 до 100 000 могут быть трехзначными, четырёхзначными и пятизначными. 1) Трехзначные числа будут состоять только из указанных цифр с различными перестановками с повторениями: 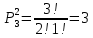 . Получаем три числа, удовлетворяющих условию: 884, 848, 488. 2) Четырехзначные числа получаются из трехзначных, составленных в первом пункте, путем установки какой-либо из оставшихся 7 цифр (исключая 0) на первую позицию, любой из оставшихся 8 цифр на вторую позицию (берём трехзначное число и вставляем между 1 и 2 цифрами другую цифру), на третью и на четвертую. Получаем 7+8+8+8 =31 вариант. Т..к. исходных трехзначных чисел было три, то всего нужных четырехзначных чисел получится 3∙31=93 варианта. 3) Пятизначные построим добавлением цифры в каждое четырехзначное из предыдущего пункта. Аналогично получаем 7 вариантов цифр для первой позиции и по 8 вариантов для второй, третьей, четвертой и пятой – всего 7+8∙4 = 39. Т.к. исходных четырехзначных чисел 93, то всего пятизначных чисел получим 39∙31=1209. 4) Суммируем получившиеся варианты трехзначных, четырехзначных и пятизначных чисел: 3+93+1209 = 1305. Ответ: 1305. №5. Сколько существует положительных трехзначных чисел: а) не делящихся ни на одно из чисел 6, 9, 15? б) делящихся ровно на одно из этих чисел? Решение. Обозначим через Р6, Р9, Р15 свойство делимости на 6, 9 и 15 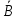соответственно;  ,  ,  – множества чисел, которые не делятся на 6, 9 и 15 соответственно.Всего трехзначных чисел 9∙10∙10=900. Чисел, кратных 6: 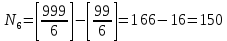 .Чисел, кратных 9: 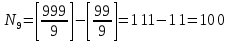 .Чисел, кратных 15:  .НОК(6,9)=18, следовательно, чисел, кратных 6 и 9:  .НОК (9,15)=45, следовательно, чисел, кратных 9 и 15: 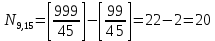 .НОК(6,15)=30, следовательно, чисел, кратных 6 и 15: 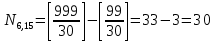 .НОК(6,9,15)=90, следовательно, чисел, кратных 6, 9 и 15: 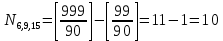 .Количество трехзначных чисел, не делящихся ни на одно из чисел 6, 9, 15, можно найти по формуле включений и исключений: N(0) = N – (N6+N9+N15) + (N6,9+N9,15+N6,15) – N6,9,15 = = 900 – (150+100+60) + (50+20+30) – 10 = 680. Найдем количество трехзначных чисел, делящихся ровно на одно из чисел 6, 9, 15. Используем формулу вычисления числа N(r) элементов, обладающих ровно r свойствами (1≤r≤m): 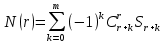 .Получим: N(1) =  ∙ S1 +  S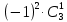2 +  S3 == (N6+N9+N15) – 2(N6,9+N9,15+N6,15) + 3N6,9,15 = = (150+100+60) – 2(50+20+30) + 3∙10 = 140. Ответ: а) 680; б) 140. №6. Найти коэффициенты при a=x2∙y2∙z4, b=x2∙y∙z6, c=x4∙y2 в разложении (5x+4y+z2)6. Решение. Применим полиномиальную формулу  Тогда коэффициенты при членах разложения можно вычислить по формуле 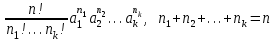 .Для члена разложения a=x2∙y2∙z4 получим:   Для b=x2∙y∙z6 получим:   Для c=x4∙y2 получим: 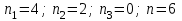 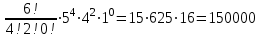 Ответ: 36000; 6000; 150000. |