Решение Определение показателя политропы, где к показатель адиабаты, для воздуха к 1,4
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
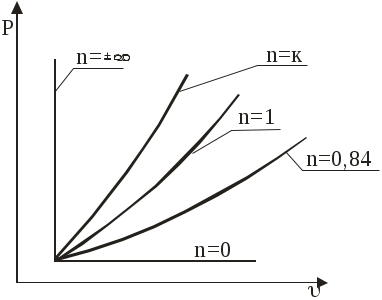
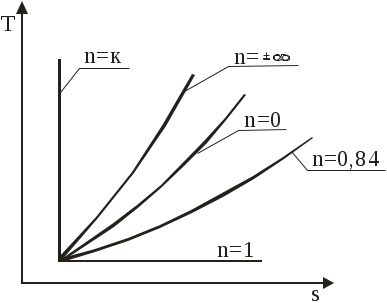
Задача 1. В процессе изменения состояния 1 кг газа (воздуха) внутренняя энергия его увеличивается на Δu = 4 кДж/кг. При этом над газом совершается работа, равная l = 10 кДж/кг. Начальная температура газа t1 = 170С, конечное давление р2 = 0,7 МПа. Определить для заданного газа показатель политропы n, начальные и конечные параметры, изменение энтропии Δs и изменение энтальпии Δh. Представить процесс в p – vи T - s- диаграммах. Изобразите также (без расчета) изобарный, изохорный, изотермический и адиабатный процессы, проходящие через ту же начальную точку, и дать их сравнительный анализ. Решение: 1. Определение показателя политропы: где к – показатель адиабаты, для воздуха к = 1,4. 2. Определение начальных и конечных параметров где R – газовая постоянная, Дж/кг, для воздуха R = 287 Дж/кг. Т1 = t1 + 273 = 17 + 273 = 290 К; 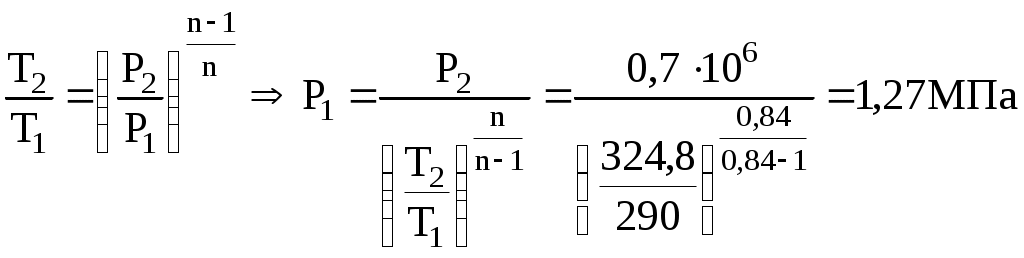 ; ;3. Определение изменения энтропии где сv – массовая изохорная теплоемкость, Дж/кгК. где μсν – мольная изохорная теплоемкость, кДж/кмольК, для воздуха μсν = 20,93 кДж/кмольК; μ – молярная масса, для воздуха μ = 28,96. Тогда 4. Определение изменения энтальпии где ср – массовая изобарная теплоемкость, Дж/кгК. где μср – мольная изохорная теплоемкость, кДж/кмольК, для воздуха μсν = 29,31 кДж/кмольК.
Задача 2. Определить параметры рабочего тела в характерных точках идеального цикла поршневого двигателя внутреннего сгорания с изохорно-изобарным подводом теплоты (смешанный цикл), если известны давление р1 = 0,135 МПа и температура t1 = 25оС рабочего тела в начале сжатия. Степень сжатия ε = 16,0, степень повышения давления λ = 2,1, степень предварительного расширения ρ = 1,4. Определить работу, получаемую от цикла, его термический КПД и изменение энтропии отдельных процессов цикла. За рабочее тело принять воздух, считая теплоемкость его в расчетном интервале температур постоянной. 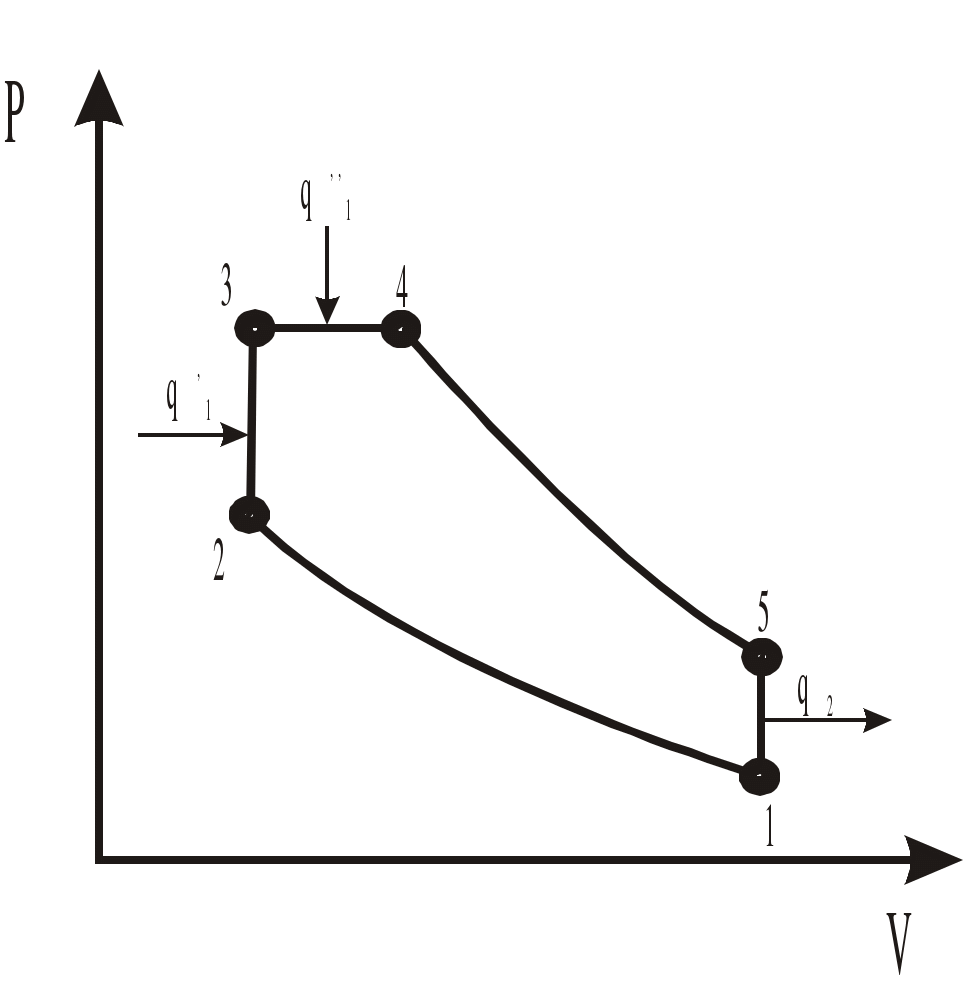 Рис. 1. Идеальный цикл поршневого двигателя внутреннего сгорания с изохорно-изобарным расширением Решение: Точка 1. р1 = 0,135 Мпа, Т1 = t1 + 273 = 25 + 273 = 298 К. Из уравнения состояния газа определяем первоначальный удельный объем Газовая постоянная воздуха, определится где в – молярная масса воздуха, кмоль, в = 28,96 кмоль. Тогда  Точка 2. Процесс 1 – 2 адиабатное сжатие. 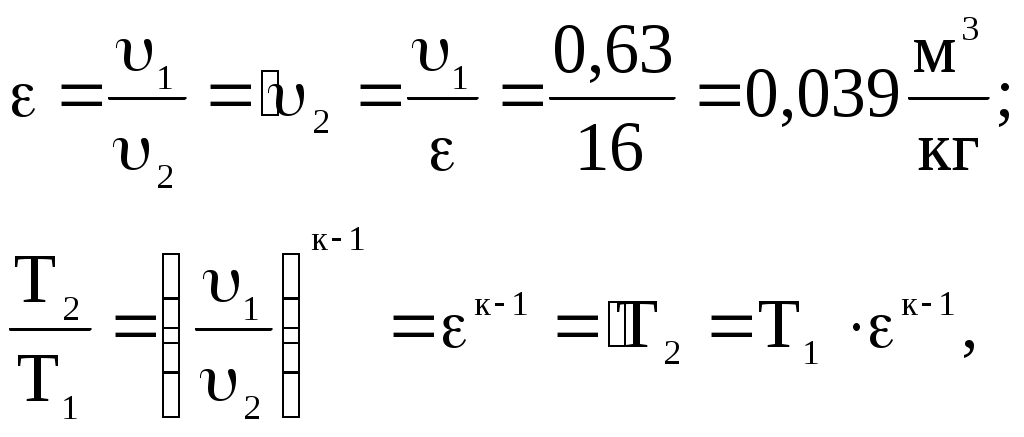 где к – показатель адиабаты, для воздуха к = 1,4. Т2 = 298 161,4 – 1 = 903,4 К. Давление в конце адиабатического сжатия определяем из уравнения состояния газа 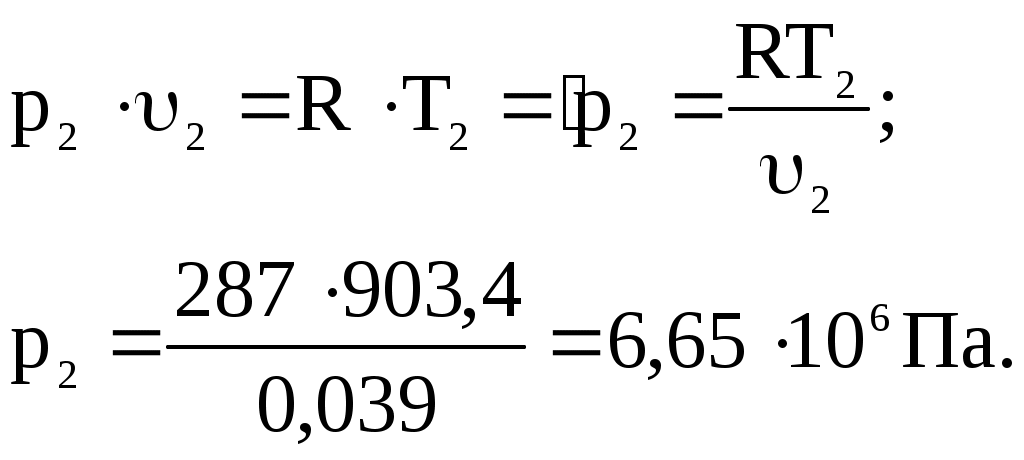 Точка 3. Процесс 2 –3 изохорный, т.е. = const. Тогда 2 = 3 = 0,039 Давление находим из соотношения Так как 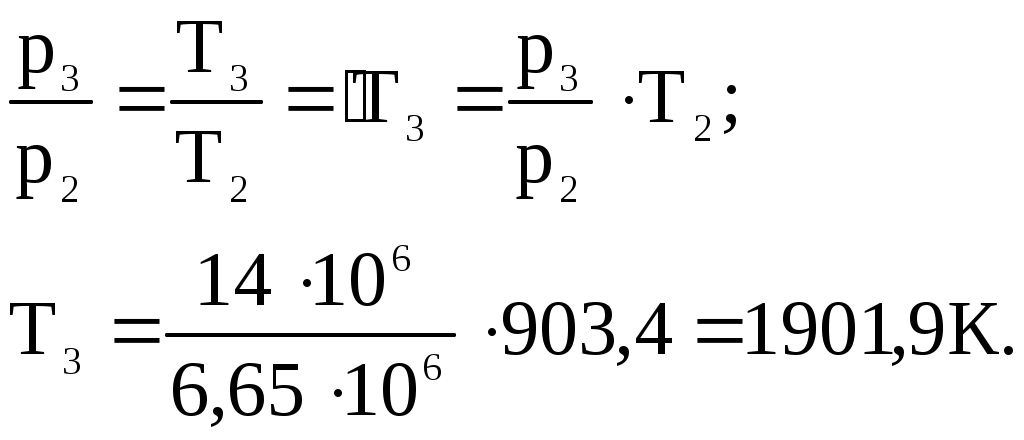 Точка 4. Процесс 3 – 4 изобарный, т.е. р = const. Тогда р3 = р4 = 14 106 Па. Объем и температура определятся из соотношения 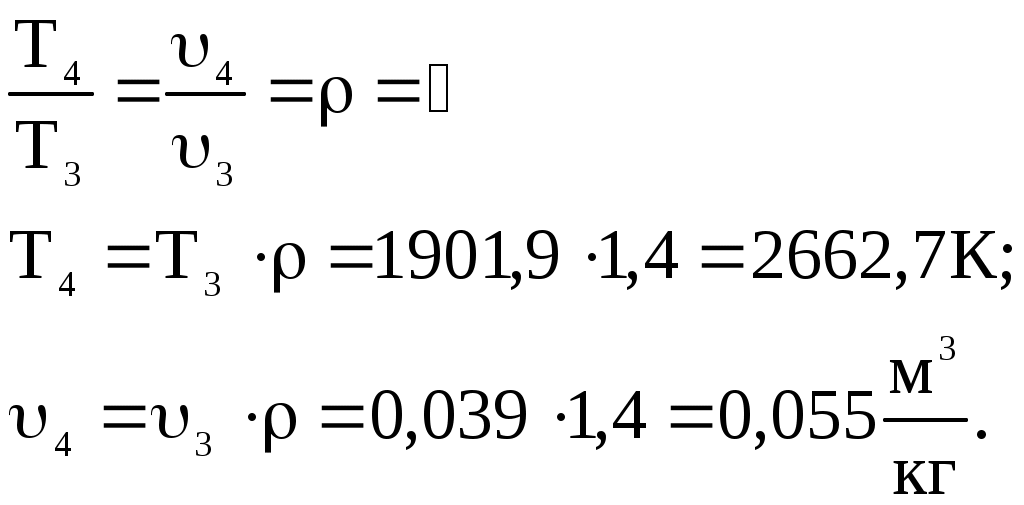 Точка 5. Процесс 4 – 5 адиабатное сжатие. Зависимость между объемами и температурами запишется в виде 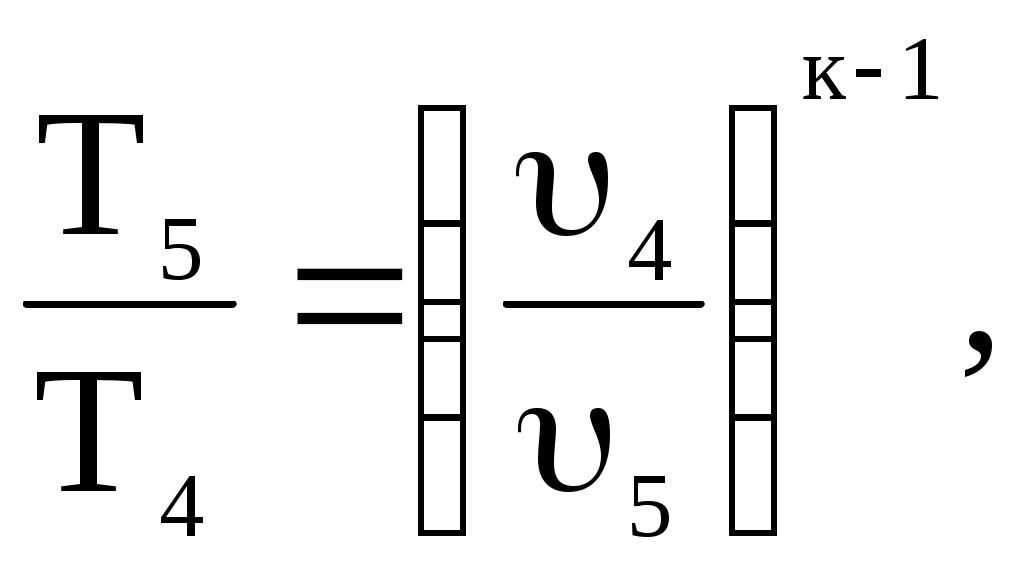 причем 4 = 2 ; 5 = 1 = 0,63 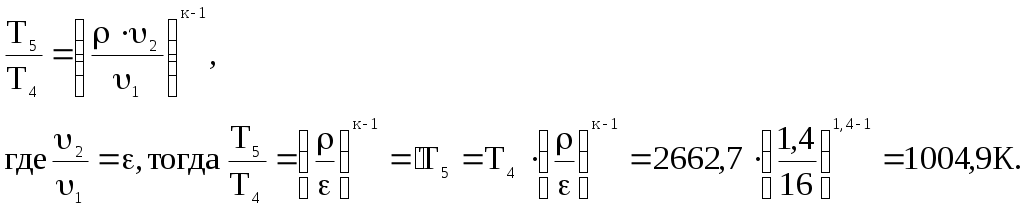 Давление определяем из уравнения состояния газа для 1 кг. Работа цикла может быть определена как разность между работой расширения и работой сжатия. Работа определится l = q1 – q2, где q1 – количество теплоты, подводимое к рабочему телу, кДж; q2 - количество теплоты, отводимое от рабочего тела, кДж. q1 = q1 + q1 = С(Т3 – Т2) + Ср(Т4 – Т3), где С - массовая теплоемкость при постоянном объеме, Ср - массовая теплоемкость при постоянном давлении, где С - мольная теплоемкость при постоянном объеме, Тогда где Ср - мольная теплоемкость при постоянном давлении, Тогда q1 = 0,72(1901,9 – 903,4) + 1,01(2662,7 – 1901,9) = 1487,3 q2 = С(Т5 – Т1) = 0,72(1004,9 – 298) = 509 Работа цикла Термический КПД цикла равен Определяем изменение энтропии в различных процессах - для процессов 1 - 2 и 4 - 5 S1 - 2 = 0 и S4 - 5 = 0, т.к. процесс адиабатический; - для процесса 2 - 3 - для процесса 3 - 4 - для процесса 5 - 1 Задача 3. Смесь газов с начальной температурой t1 = 25°С сжимается в одноступенчатом поршневом компрессоре от давления р1 = 0,1 МПа до давления р2 = 0,95 МПа. Сжатие может проходить по изотерме, по адиабате и по политропе с показателем политропы n = 1,33. Определить для каждого из трех процессов сжатия конечную температуру газа t2, отведенное от смеси тепло Q кВт, изменение внутренней энергии и энтропии смеси и теоретическую мощность компрессора, если его производительность G = 0,3 × 10-3кг/ч. Дать сводную таблицу и изображение процессов сжатия в p - v и T - s - диаграммах, а также какое количество воды необходимо прокачивать через рубашку цилиндра при сжатии газа по изотерме и по политропе, если температура воды при этом повышается на 20°С? Состав смеси: 2кгО2 + 8кг N2. Указание. Расчет провести без учета зависимости теплоемкости от температуры. Решение: 1. Определяем газовую постоянную смеси 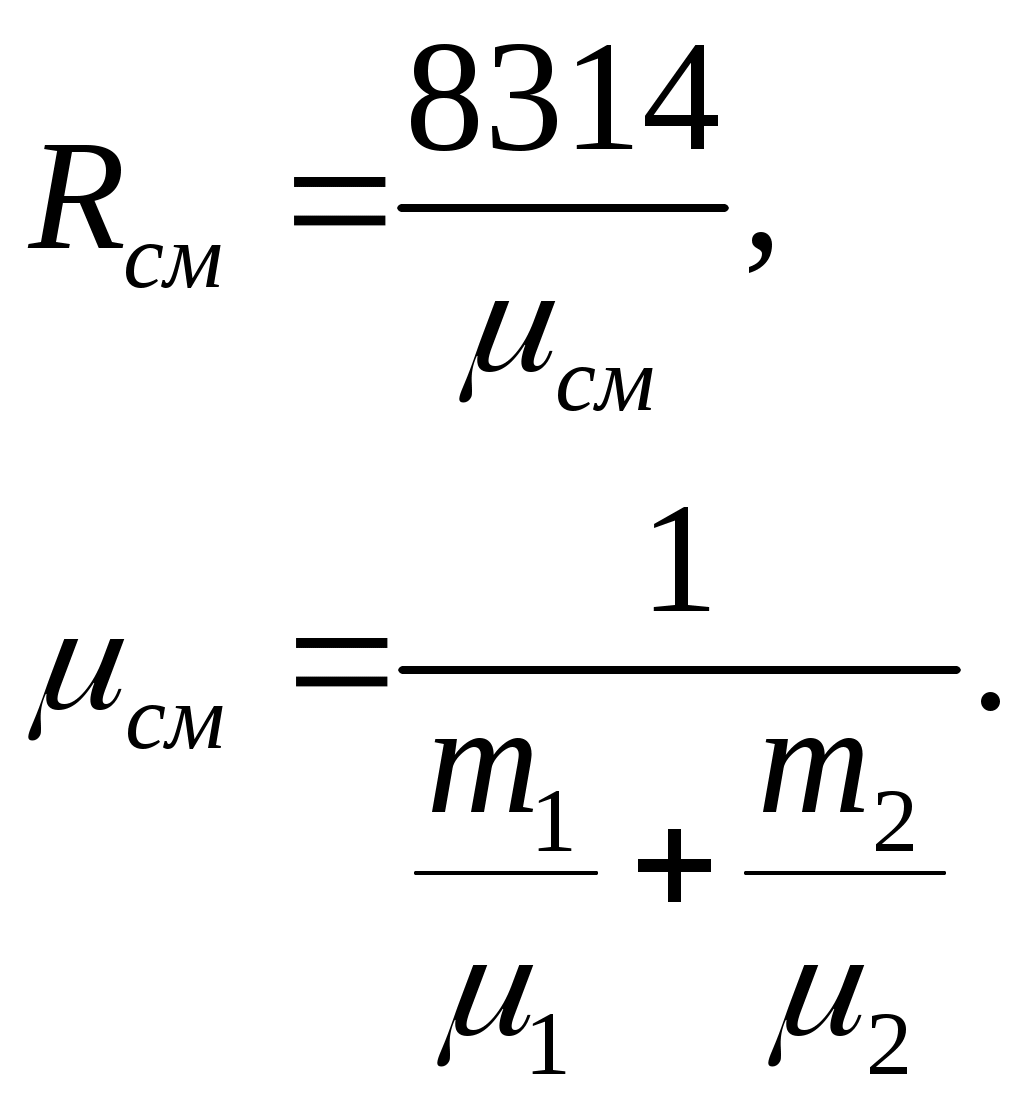 массовые доли определятся как: 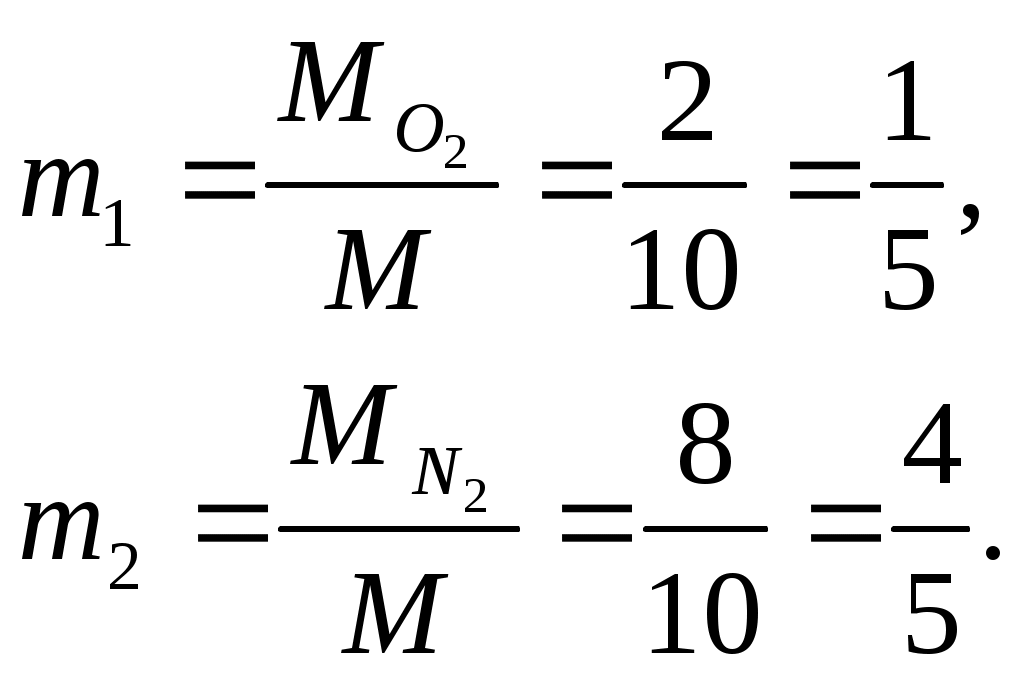 Молярная масса кислорода 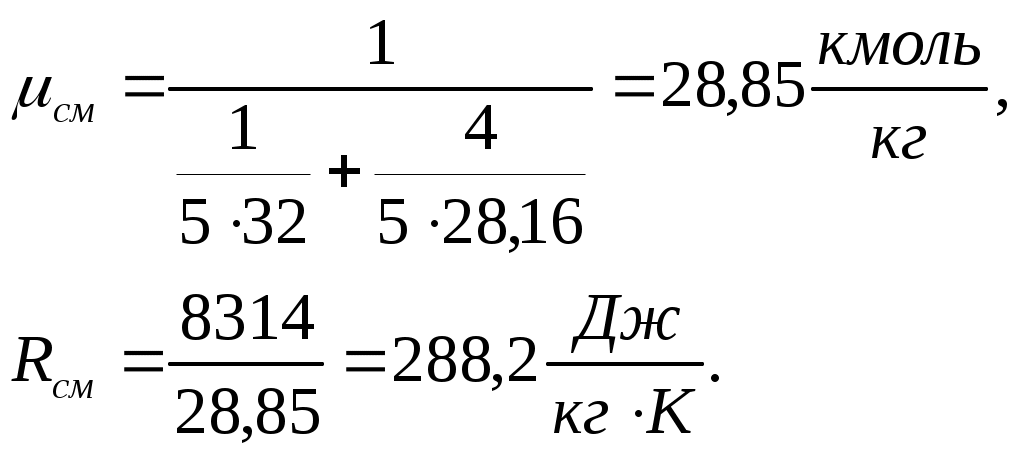 2. Определение первоначального объема смеси ν1. 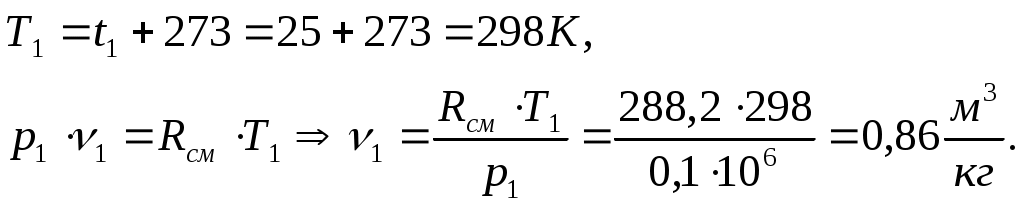 3. Сжатие компрессора по изотерме Т2 = Т1 = 298 К. - теоретическая работа компрессора определится 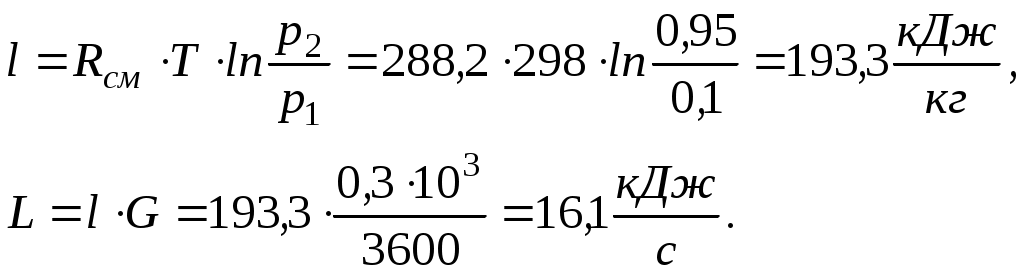 - изменение внутренней энергии ΔU = 0 - изменение энтропии смеси 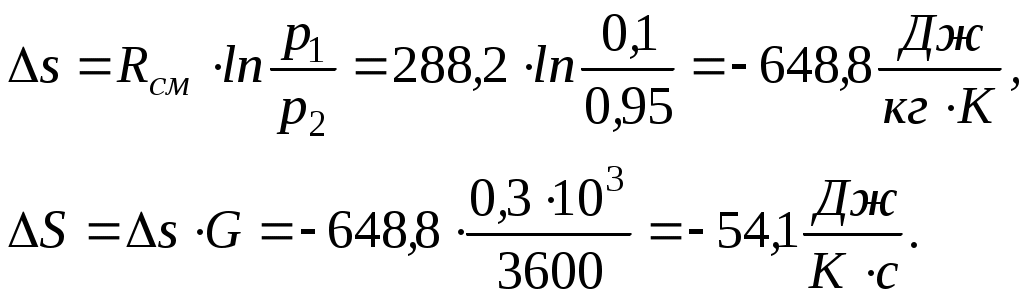 - количество отведенного от смеси тепла - теоретическая мощность компрессора N = Q = 16,1 кВт. 4. Сжатие компрессора по адиабате. к = 1,4 – показатель адиабаты. - конечная температура 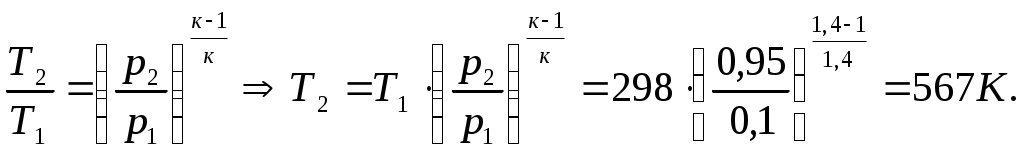 - теоретическая работа компрессора 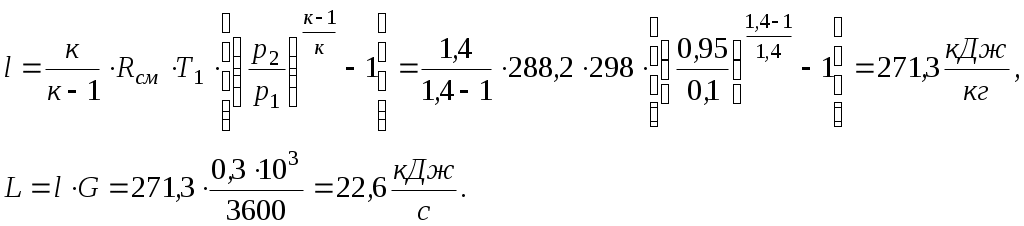 - изменение внутренней энергии Δu = сυсм(Т2 – Т1), 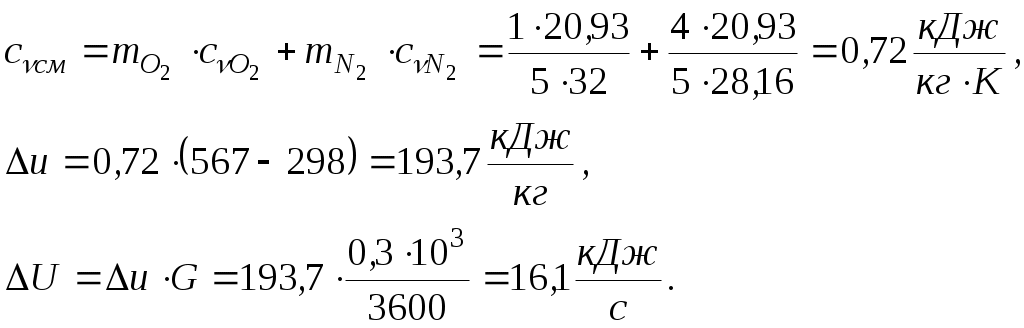 - изменение энтропии смеси ΔS = 0. - количество отведенного от смеси тепла dQ = 0. - теоретическая мощность компрессора 5. Сжатие компрессора по политропе. n = 1,33 – показатель политропы. - конечная температура 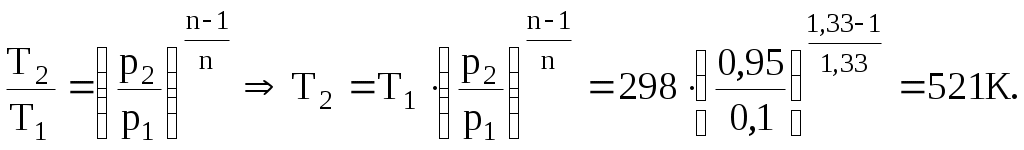 - теоретическая работа компрессора 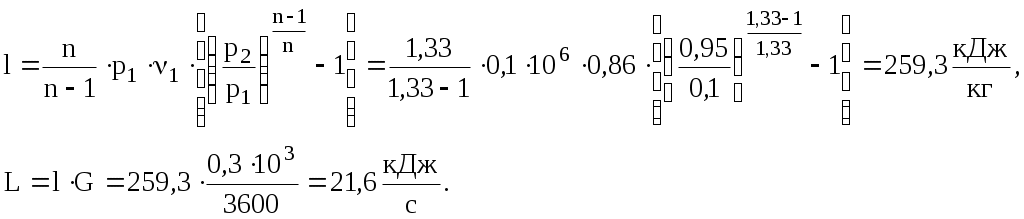 - теоретическая мощность компрессора - теоретическая мощность компрессора- количество отведенного от смеси тепла Δu = сυ (Т2 – Т1) = 0,72·103·(521-298) = 160,6 кДж/кг. - изменение энтропии смеси 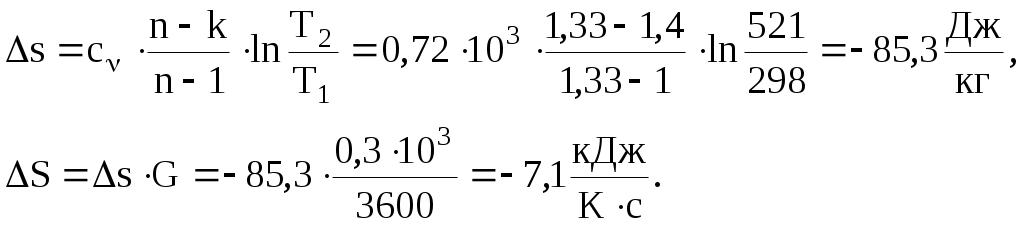 6. Количество воды, которое необходимо прокачивать через рубашку цилиндра при сжатии: - по изотерме где св = 4,19 кДж/(кг·К) – теплоемкость воды. - по политропе Задача 4. Определить потребную поверхность рекуперативного теплообменника, в котором вода нагревается горячими газами. Расчет произвести для противо-точной и прямоточной схем. Привести графики изменения температур для обеих схем движения, если расход воды 2,5 кг/с. Значения температур газа Коэффициент теплопередачи К = 20 Вт/(м2·К). Решение: Количество теплоты переданное от газов к воде при заданных условиях равно: откуда Определим количество теплоты, полученное водой при нагревании воды с 20°С до 100°С в теплообменнике. Для определения температурного напора построим графики изменения температур 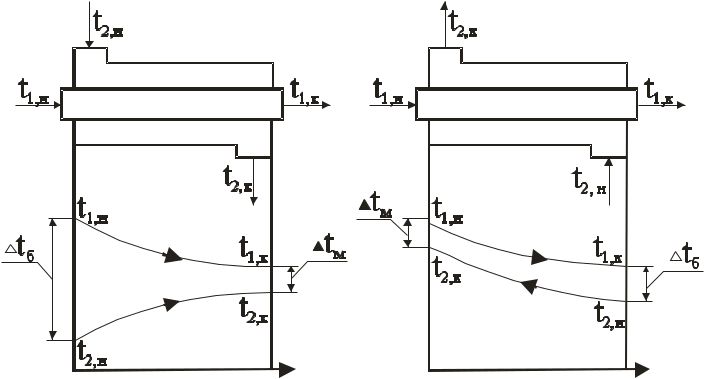 прямоток противоток прямоток противотокРис. 2. Графики изменения температур Для прямотока: Δtб = t1,н – t2,н = 450 – 20 = 430°С; Δtм = t1,к – t2,к = 225 – 100 = 125°С; Для противотока: Δtб = t1,н – t2,к = 450 – 100 = 350°С; Δtм = t1,к – t2,н = 225 – 20 = 205°С; В обоих случаях 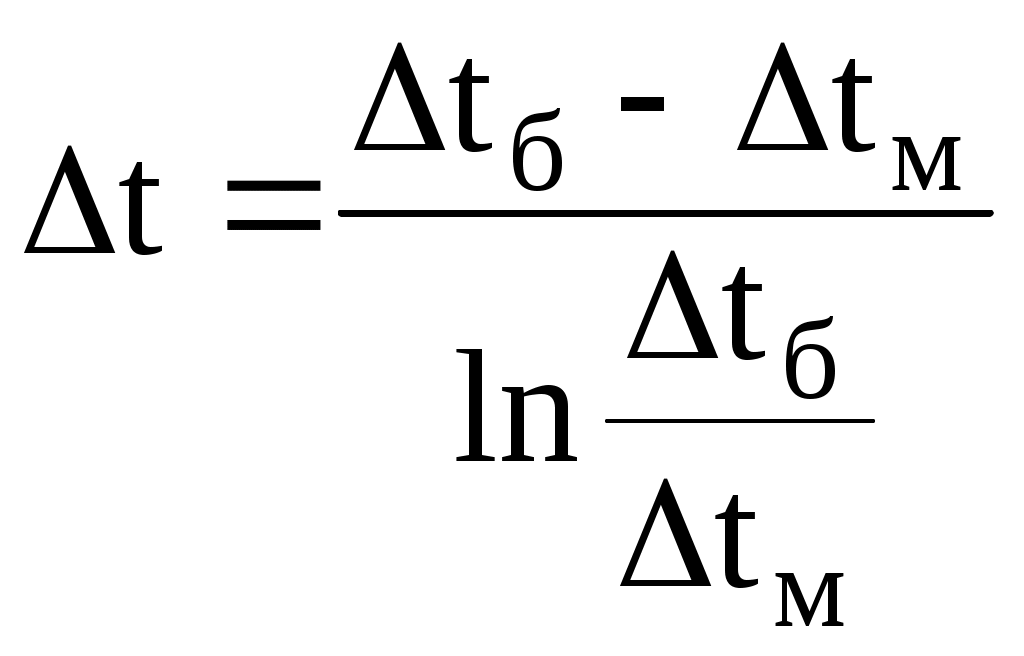 . .Тогда для прямотока: 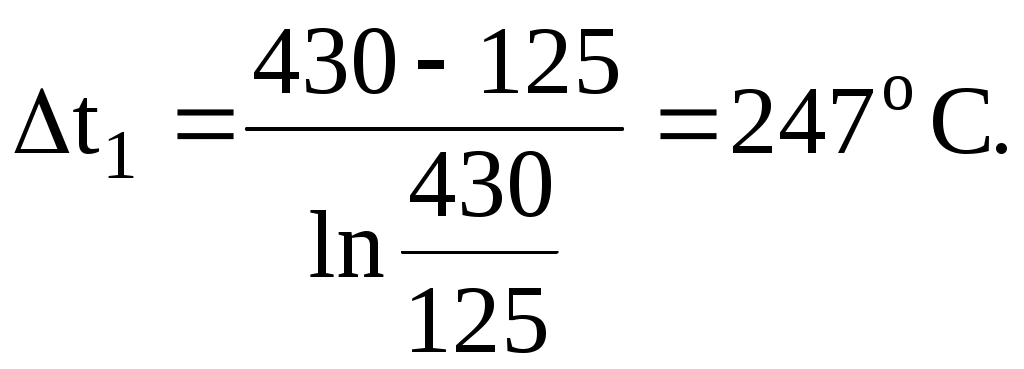 Для противотока: 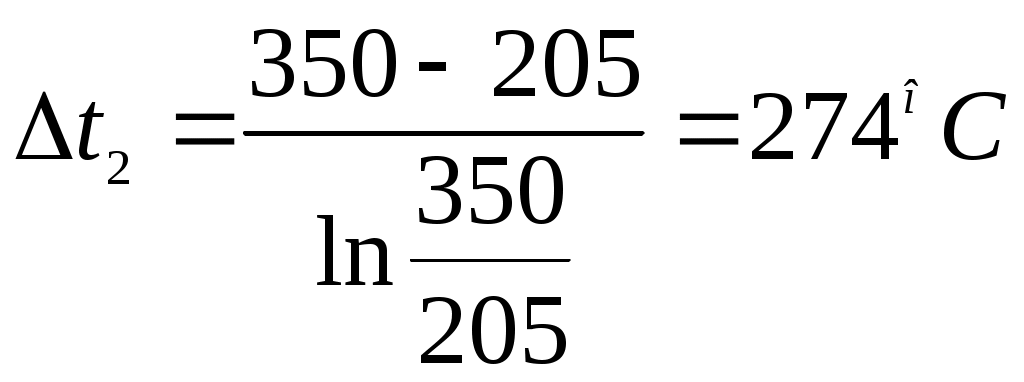 . .Следовательно, потребная поверхность рекуперативного теплообменника равна: для прямотока: для противотока Значит, при одинаковых выходных тепловых параметрах на изготовление противоточного теплообменника требуется значительно меньше материала. Задача 5. Рассчитать теплопотребление производственного корпуса на 100 грузовых автомобилей размером 60х36х7,2 м с 2х этажным пристроем – административно – бытовым корпусом 18х12х7,2 м с количеством рабочих, равным 50 человек. Решение: Определяем максимальный расход теплоты, расходуемой на отопление производственного здания: Фот = qот Vн(tв - tн) а,кВт, где qот = 0,6 Вт/м3 К – удельная отопительная характеристика здания (таблица 2. Приложения); Vн = 15552 м3 – объем здания по наружному обмеру; tв = 200С – внутренняя расчетная температура; tн = -350С – наружная температура воздуха (для условий Кировской области); а = 0,54 + 22/(tв - tн) = 0,54 + 22 / 20-(-35) = 0,58 – поправочный коэффициент, учитывающий влияние на удельную тепловую характеристику местных климатических условий. ТогдаФот = 0,6 1555220-(-35) 0,58 = 297,7 кВт. Находим максимальный расход теплоты на отопление общественного помещения Фот = 0,5 155520-(-35) 0,58 = 24,8 кВт. Определяем максимальный поток теплоты на вентиляцию производственного здания. Фв = qв Vн(tв - tн.в) , кВт, где qв = 0,2 Вт/м3К – удельная вентиляционная характеристика здания (таблица 2. Приложения). Фв = 0,2 1555220-(-35) = 171 кВт. Расход теплоты на горячее водоснабжение на один автомобиль в производственном помещении определится: Фг.в.пр = 0,278Vг.в. Св(tг – tх) , Вт, где Vг.в = 250 л/сут = 10,4 кг/ч – часовой расход горячей воды. Св = 4,187 кДж/кгК – теплоемкость воды при t = 550С [2]; tг = 550С – расчетная температура горячей воды; tх = 50С – расчетная температура холодной воды. Тогда Фг.в.пр = 0,27810,44,187(55-5) = 0,605кВт. На 100 грузовых автомобилей Фг.в.пр = 0,605100 = 60,5 кВт. Максимальный расход теплоты на горячее водоснабжение общественного здания: Фг.в.о = 2 Фг.в.ср= 216 = 32 кВт, где Фг.в.ср = qг.в.n = 50320 = 16000 Вт, где n = 50 – количество рабочих; qг.в.= 320 Вт – укрупненный показатель. В летний периодФг.в.об = 0,65 Фг.в.о= 0,6532 = 20,8 кВт, Фг.в.пр = 0,82 Фг.в.пр = 0,8260,5 = 49,6 кВт. Определяем расход теплоты на технологические нужды автопредприятия: Фт = 0,278G(i - квiвод), Вт, где т - коэффициент спроса на теплоту, равный 0,6…0,7, принимаем = 0,65; G – расход теплоносителя, кг/ч; i – энтальпия теплоносителя, кДж/кг. Принимаем i = 398 кДж/кг для воды при t = 950С [2]; iвод = 280 кДж/кг – энтальпия обратной воды [2]; кв = 0,7 – коэффициент возврата обратной воды. Расход теплоносителя (воды при t = 950С) для получения смешанной воды с температурой tсм = 600С равен: где tx = 100C – температура холодной воды; Gсм = nq/24 кг/ч – количество смешанной воды; n – число автомобилей, подвергающихся мойке в течение суток. Принимаем n = 20 автомобилей. Q = 250 кг/сут – среднесуточный расход воды на мойку одного автомобиля. Тогдаа Следовательно Фт = 0,2780,65122,4(398-0,7280) = 4450 Вт = 4,5 кВт. Средневзвешенная расчетная температура равна tв.ср = (1555218 + 155520) / 17107 = 180С. Строим годовой график потребления теплоты производственного корпуса на 100 грузовых автомобилей. 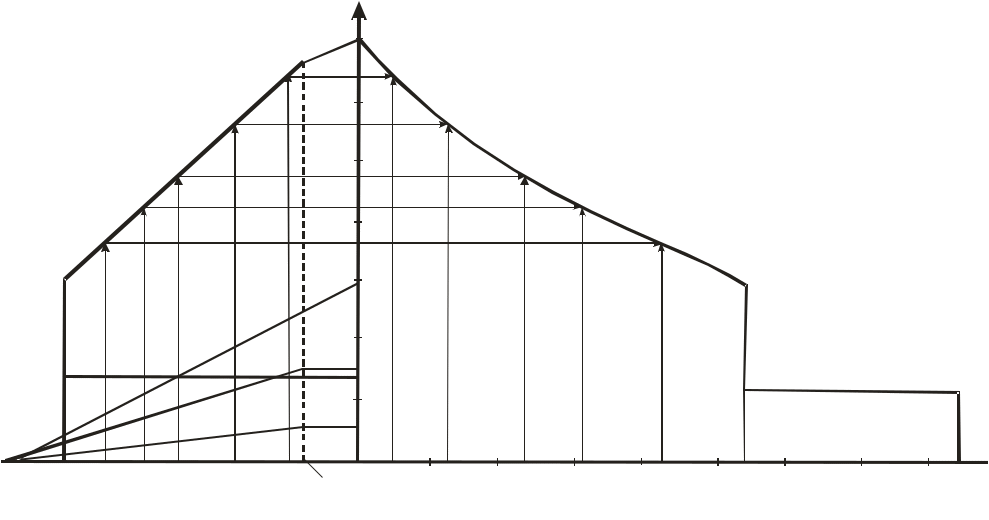 Рис. 3. Годовой график потребления тепла производственным корпусом на 100 грузовых автомобилей. Находим суммарный годовой расход теплоты: Qгод = 3,610-6F mсрmi , ГДж/год, где F = 4178 мм2 – площадь годового графика; mср = 8,3 Вт/мм – масштаб расход теплоты: mi = 66,7 ч/мм – масштаб времени потребления теплоты. Тогда Qгод = 3,610-641788,366,7 = 8,7 ГДж/год ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ Задача 1. В процессе изменения состояния 1 кг газа внутренняя энергия его увеличивается на Δu. При этом над газом совершается работа, равная l. Начальная температура газа t1, конечное давление р2. Определить для заданного газа показатель политропы n, начальные и конечные параметры, изменение энтропии Δs и изменение энтальпии Δh. Представить процесс в p – vи T - s- диаграммах. Изобразите также (без расчета) изобарный, изохорный, изотермический и адиабатный процессы, проходящие через ту же начальную точку, и дать их сравнительный анализ. Данные для решения задачи выбрать из таблицы 1. Таблица 1
Контрольный вопрос. Какова общая формулировка и математическое выражение первого закона термодинамики? Задача 2. Определить параметры рабочего тела в характерных точках идеального цикла поршневого двигателя внутреннего сгорания с изохорно-изобарным подводом теплоты (смешанный цикл), если известны давление р1 и температура t1 рабочего тела в начале сжатия. Степень сжатия ε, степень повышения давления λ, степень предварительного расширения ρ заданы. Определить работу, получаемую от цикла, его термический КПД и изменение энтропии отдельных процессов цикла. За рабочее тело принять воздух, считая теплоемкость его в расчетном интервале температур постоянной. Построить на "миллиметровке" в масштабе этот цикл в координатах p - v и T - s. Дать к полученным диаграммам соответствующие пояснения. Данные для решения задачи выбрать из таблицы 2. Таблица 2
Контрольный вопрос. В чем смысл второго закона термодинамики? Задача 3. Смесь газов с начальной температурой t1 = 27°С сжимается в одноступенчатом поршневом компрессоре от давления р1 = 0,1 МПа до давления р2. Сжатие может проходить по изотерме, по адиабате и по политропе с показателем политропы n. Определить для каждого из трех процессов сжатия конечную температуру газа t2, отведенное от смеси тепло Q кВт, изменение внутренней энергии и энтропии смеси и теоретическую мощность компрессора, если его производительность G. Дать сводную таблицу и изображение процессов сжатия в p - v и T - s - диаграммах, а также какое количество воды необходимо прокачивать через рубашку цилиндра при сжатии газа по изотерме и по политропе, если температура воды при этом повышается на 20°С? Данные, необходимые для решения задачи, выбрать из таблицы 3. Указание. Расчет провести без учета зависимости теплоемкости от температуры. Таблица 3
Контрольный вопрос. В каком из процессов сжатия мощность, затрачиваемая на привод компрессора, будет больше? Задача 4. Определить потребную поверхность рекуперативного теплообменника, в котором вода нагревается горячими газами. Расчет провести для прямоточной и противоточной схем. Привести графики изменения температур для обеих схем движения. Значения температур газа t'1 и t"1, воды t'2 и t"2, расхода воды М и коэффициента теплопередачи К выбрать из таблицы 4. Таблица 4
Контрольный вопрос. Какая из схем теплообменников (прямоточная или противоточная) имеет меньшую поверхность и почему? Задача 5. Рассчитать теплопотребление производственного корпуса на N грузовых автомобилей размером LхBхH м с 2х этажным пристроем – административно-бытовым корпусом L1хB1хH1 м с количеством рабочих, равным M человек. Данные, необходимые для решения задачи, выбрать из таблицы 5. Таблица 5
Контрольный вопрос: Эффективность систем отопления |