Документ Microsoft Word. Решение Определение приращений координат. XХ 2 х 1 230,70320,5089,80 м
 Скачать 26.14 Kb. Скачать 26.14 Kb.
|
|
Найти расстояние между двумя точками и направление этой линии (румб, азимут), если координаты начала и конца линии следующие: Х1 =320,50 м; Х2=230,70 м; Y1=780,20 м; У2=900,10 м. Решение: 1. Определение приращений координат. ∆X=Х2-Х1=230,70-320,50=-89,80 м ∆Y=Y2-Y1=900,10-780,20=119,90 м. Знаки приращений говорят, что линия расположена во 2 четверти (ЮВ). 2. Величина румба определяется по формуле по тангенсу найдем величину румба - 53°10'. 3. Расстояние между точками (d1-2) найдем по теореме Пифагора: Определить расстояние между двумя точками и направление этой линии, если координаты этих точек следующие: Х1 = 500,70 м; Х2 = 142,80 м; Y1 = 350,20 м; Y2 = 420,30 м. Привести поясняющий чертеж. Определить расстояние между двумя точками и направление этой линии, если координаты этих точек следующие: Х1 = 200,70 м; Х2 = 142,80 м; Y1 = 350,20 м; Y2 = 420,30 м. Привести поясняющий чертеж. Определить прямоугольные координаты последующей точки (т.2) через координаты предыдущей (т.1) по следующим данным: координаты первой точки - Х1 = 4250 м. У1 = 6730 м; расстояние до следующей точки d1-2 = 120,10 м; направление линии 1-2, т.е. её дирекционный угол –α 1-2 = 48 0 30` = r . (такую задачу называют прямой геодезической задачей). Решение: Для определения координат точки 2 сначала нужно найти приращения координат: ∆ X; ∆ У. Затем сами координаты Х2; У2. 1. Определение приращений координат. ∆ Х=d cos r = 120,10*0,6626=79,51м. ∆ У=d sin r = 120,10*0,7490=89,95м. 2. Определение координат точки 2. Х2 = Х1 + ∆ Х= 4250+79,51=4329,51м. У2 = У1 + ∆ У= 6730+89,95=6819,95м 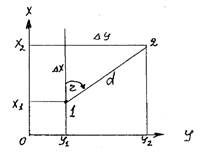 Знаки приращений координат можно определить по следующей схеме, они зависят от четверти, в которой расположена линия. СЗ СВ + ∆ Х + ∆ Х - ∆ У + ∆ У - ∆ Х - ∆ Х - ∆ У + ∆ У ЮЗ ЮВ Ю |
