Задача по сопромату. РЕШЕНИЕ_9. Решение. Определим число лишних связей (степень статической неопределимости). S С у 431
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Задание Жесткий брус, весом и деформацией которого можно пренебречь, прикреплен к неподвижной опоре и двум стержням при помощи шарниров. Определить напряжения в стержнях при следующих данных: Задача 1. Расчет системы при действии внешней силы С 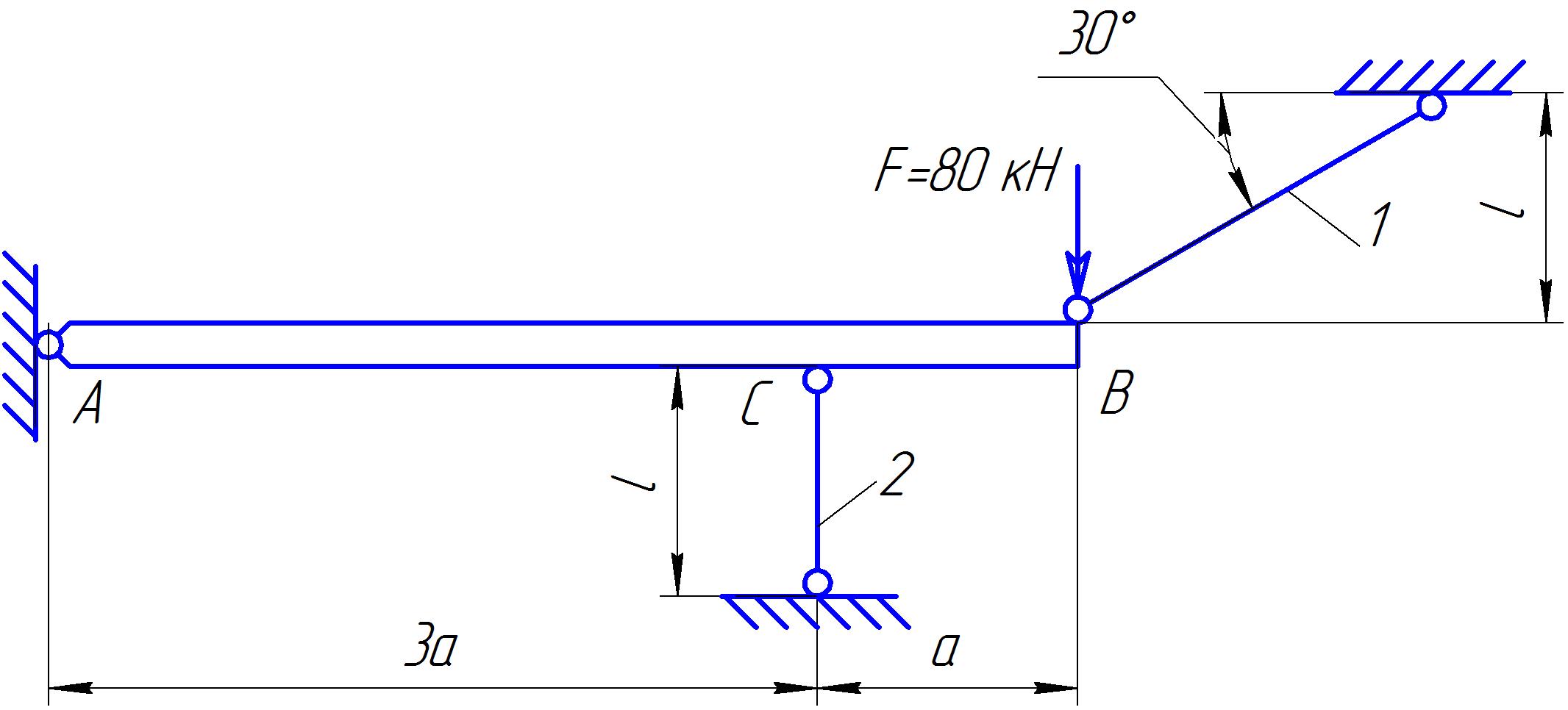 тержни стальные с площадью поперечного сечения А1 = 8∙10-4 м²; А2 = 1∙10-3 м². В правом крайнем шарнире бруса АВ приложена вертикальная сила F = 80 кН, направленная вниз. Рис. 1 Решение. 1. Определим число лишних связей (степень статической неопределимости). S = С – У = 4–3=1. Система один раз статически неопределима. Определим усилия в стержнях. Отбрасываем мысленно закрепления стержней и заменяем их действие неизвестными усилиями N1 и N2, направленными вдоль стержней(рис. 2). Ограничимся составлением одного уравнения равновесия статики (реакции опоры А определять не будем). Рис. 2 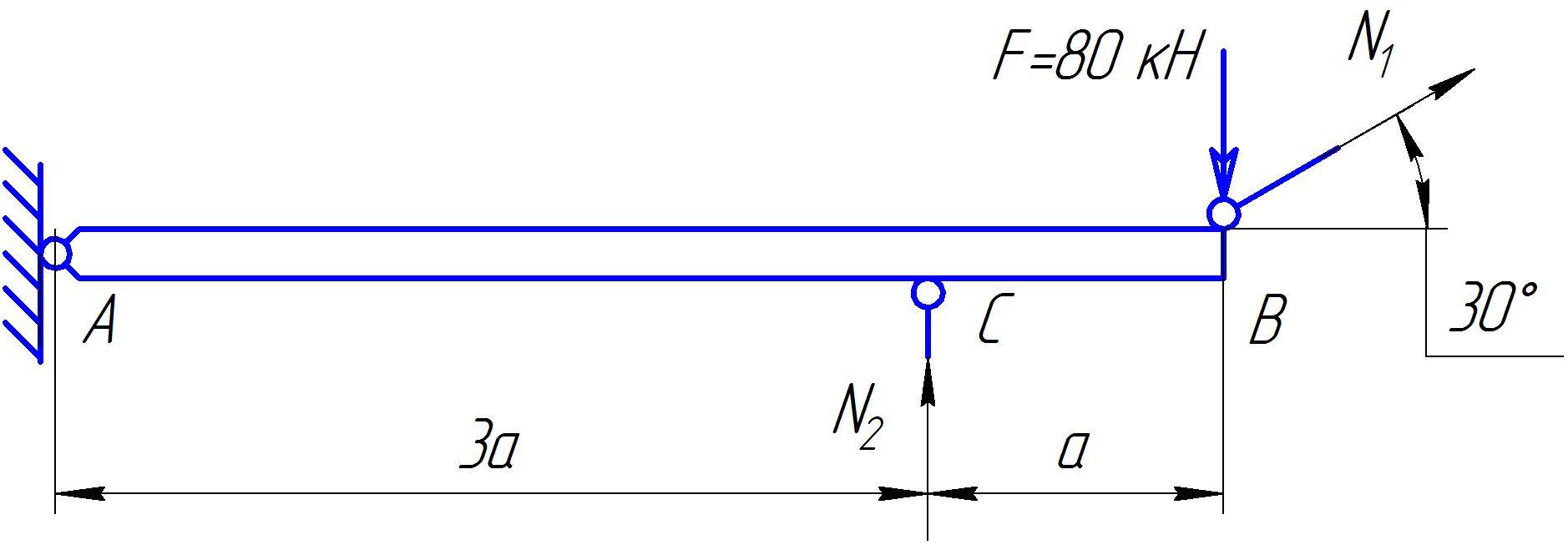 Уравнение содержит два неизвестных, для раскрытия статической неопределимости рассмотрим условие совместности деформаций и перемещений заданной системы. П 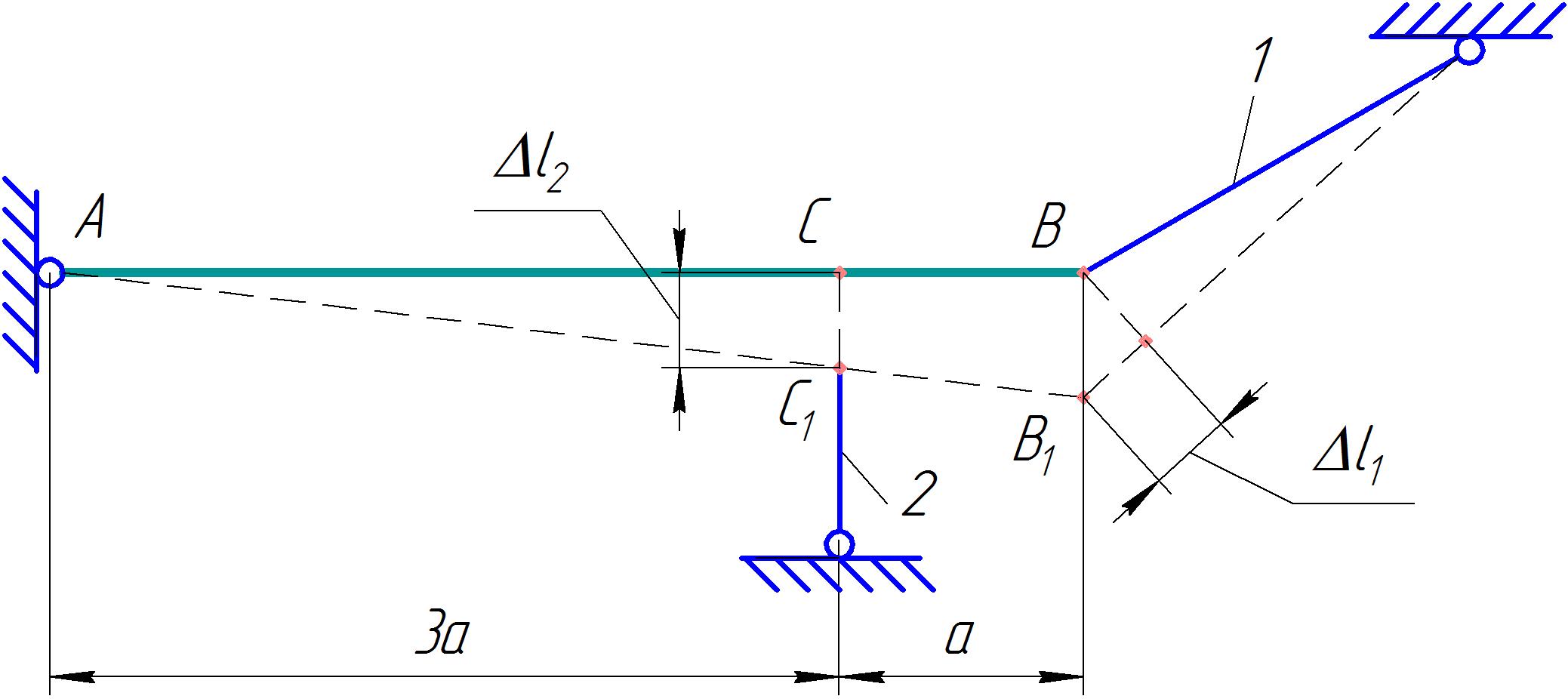 ренебрегая деформацией бруса АB (брус абсолютно жесткий), получаем при его повороте относительно опоры А под действием внешней нагрузки однозначную зависимость между перемещениями точек C и В, т.е. между деформациями стержней 1 и 2 (рис.3). Рис. 3 Стержни удлинились на величину l1иl2соответственно. Перемещение точки С в положение С1определяет деформацию l2стержня 2. Для выделения на плане перемещений системы деформации стержня 1 из конца стержня (точка В) до деформации необходимо опустить перпендикуляр на его конечное положение (пунктирная прямая). Уравнение совместности деформацией составим, используя подобие треугольников АCC1и АBВ1 : Отсюда 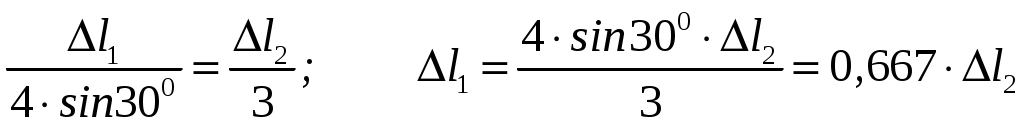 . . Выразим деформации l1иl2по закону Гука через усилия N1 и N2. 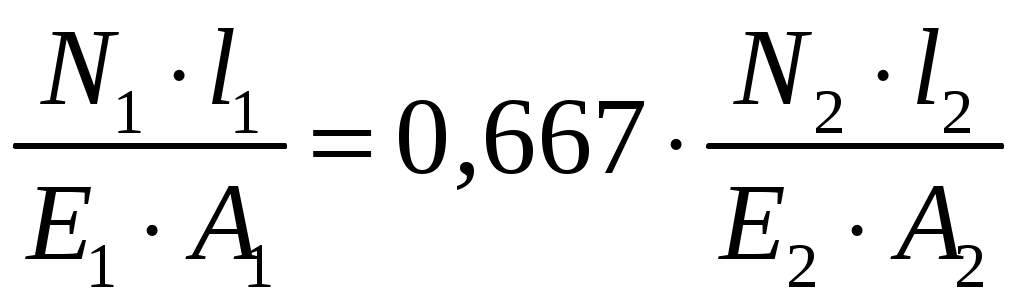 с учетом того, что 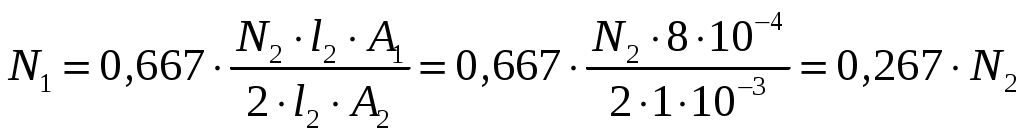 . (2) . (2)Решая совместно уравнения (1) и (2) определим искомые усилия. Подставляя 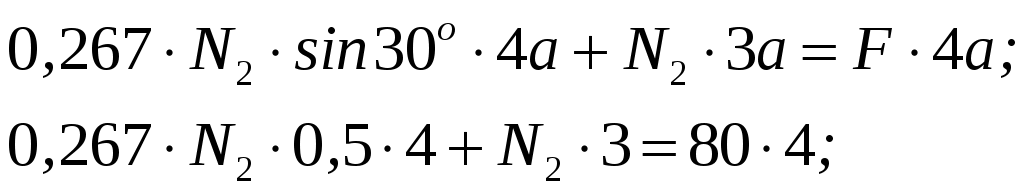 тогда Напряжения в сечении первого стержня: 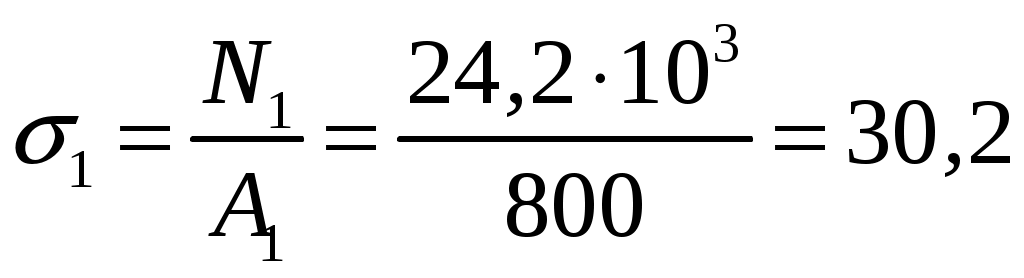 МПа; МПа;Напряжения в сечении второго стержня: 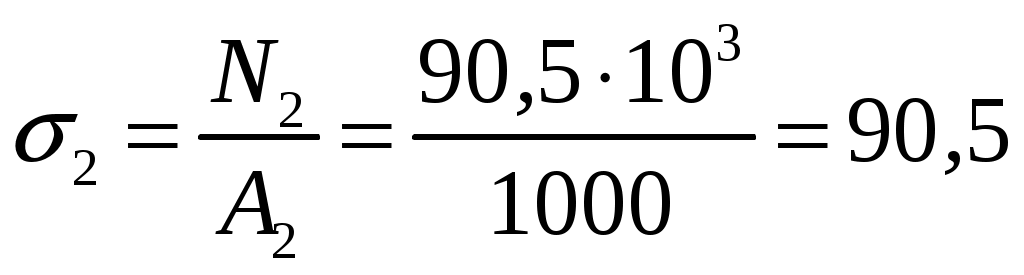 МПа. МПа.Задача 2. Расчет системы с учетом неточности изготовления стержней Стержни стальные с площадью поперечного сечения А1 = 1∙10-3 м²; А2 = 1,2∙10-3 м². Первый стержень изготовлен короче проектного размера на величину = 2 мм, модуль упругости первого рода Е = 2∙105 МПа. Д 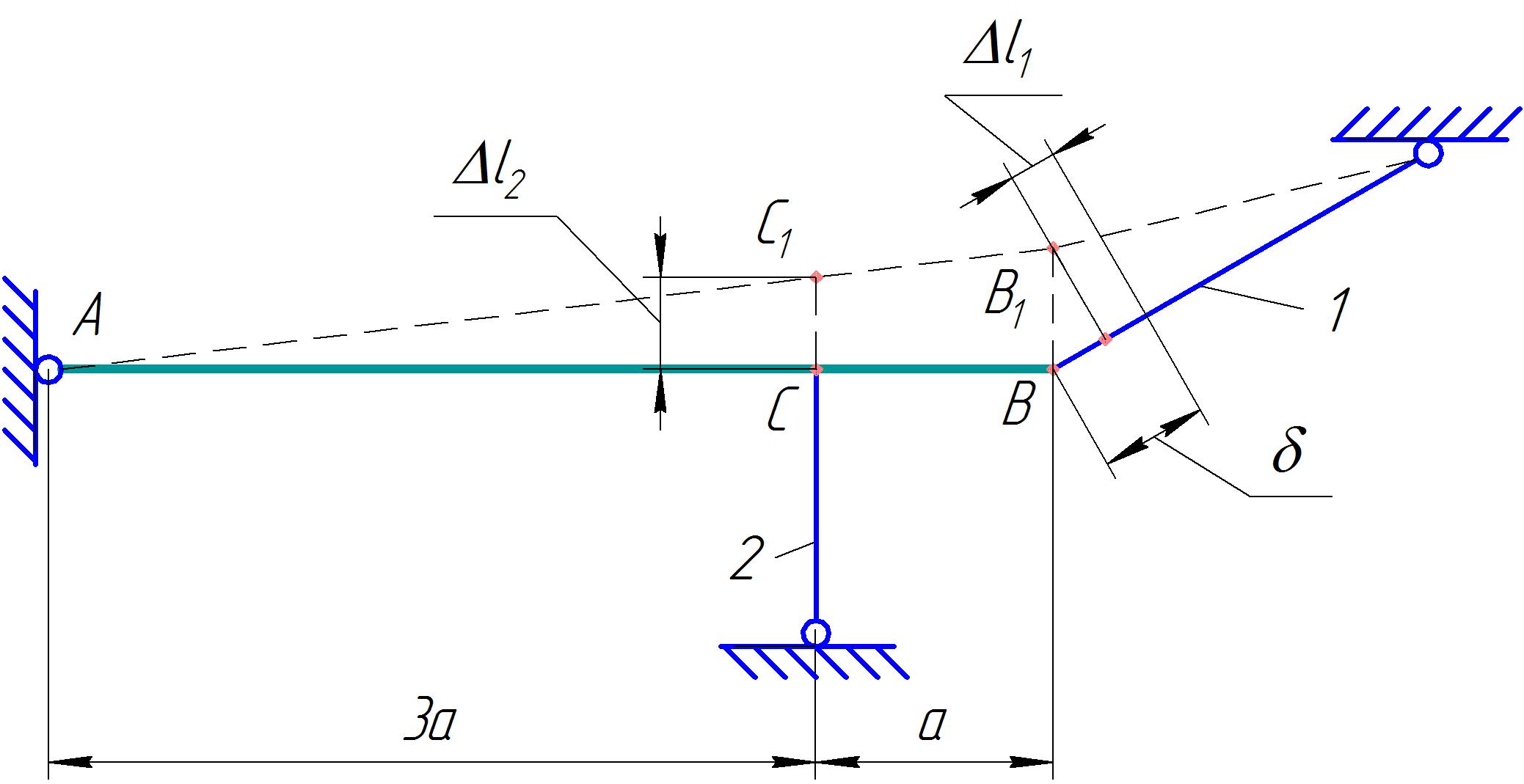 ля выяснения направления сил, которые возникают в стержнях при сборке системы, предположим, что сборку осуществили, растянув стержень 1 на Рис. 4 Когда растянутый стержень 1 был шарниром соединен с жестким брусом и внешняя нагрузка удалена, стержень в силу своей упругости поднял точку В бруса, повернув брус вокруг шарнира А и вызвал растяжение стержня 2. Полностью восстановить свою первоначальную длину стержень 1 не может - этому препятствует стержень 2, следовательно, стержень 1 остается растянутым на Dl1< Усилия в стержнях строго согласованы со схемой деформаций. Ограничимся одним уравнением статики, связывающим два неизвестных усилия: Уравнение совместности деформаций составим, рассматривая подобие треугольников АCC1и АВВ1: где 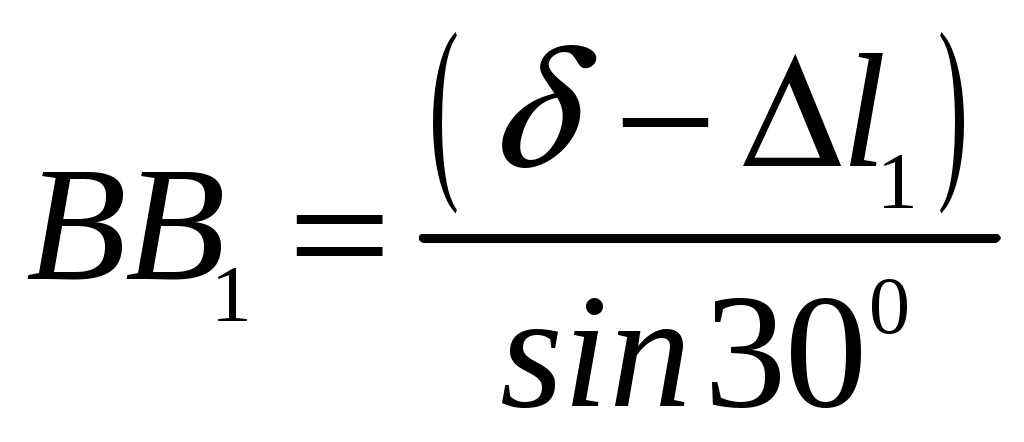 ; ; Тогда Деформации в уравнении (4) выразим по закону Гука через усилия: 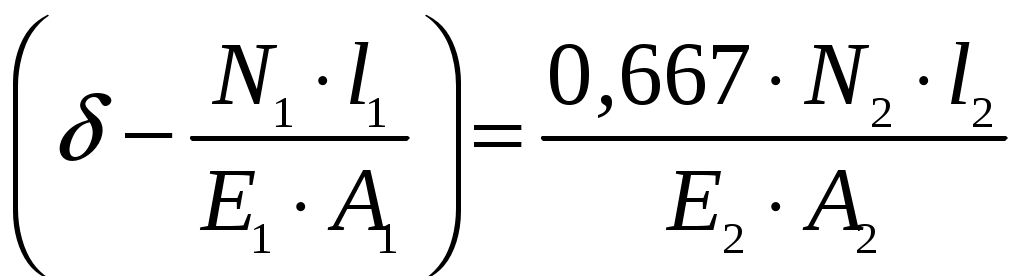 ; (5) ; (5)с учетом того, что Усилие N2: 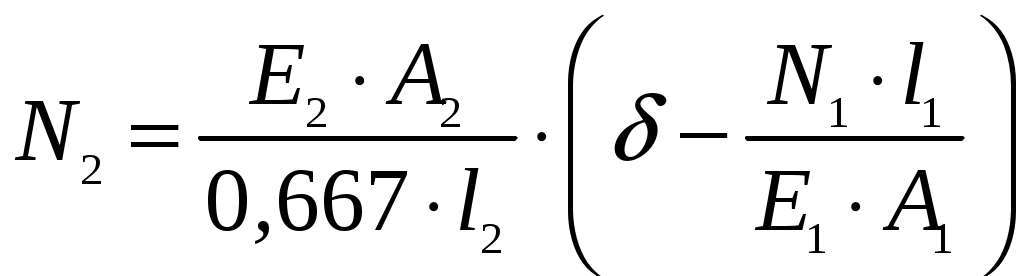 ; ;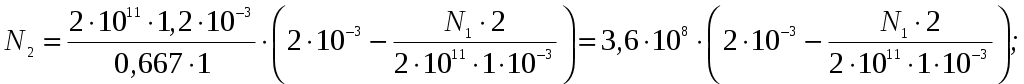 или после преобразований Подставляя этот результат в уравнение (3), находим монтажное усилие в стержне 1: Усилие в стержне 2: Монтажные напряжения в стержнях: в растянутом стержне 1: 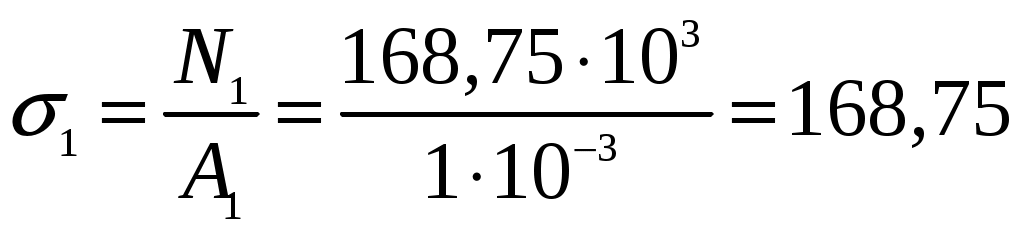 МПа; МПа;в растянутом стержне 2: 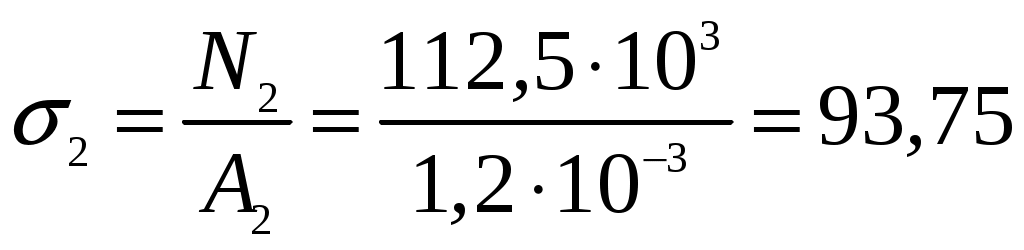 МПа. МПа.Задача 3. Расчет системы с учетом перепада температур Первый стержень стальной, второй медный. Площадь поперечного сечения А1 = А2 =1,5∙10–3 м2. Система после сборки получила отрицательный перепад температуры t = –50°С. Модули упругости ЕC = 2∙105 МПа, ЕM = 105 МПа, коэффициенты линейного расширения C = 125∙10–7 град–1; М = 160∙10–7 град–1. Так, как температура системы понижается, то оба стержня будут укорачиваться от понижения температуры. При укорочении стержней, они будут воздействовать друг на друга через недеформируемый стержень АB. Вследствие этого, в обоих стержнях будут возникать дополнительные силы растяжения. Представим систему в деформированном виде (рисунок 5). При охлаждении на 50°С стальной стрежень укоротился бы на величину Т 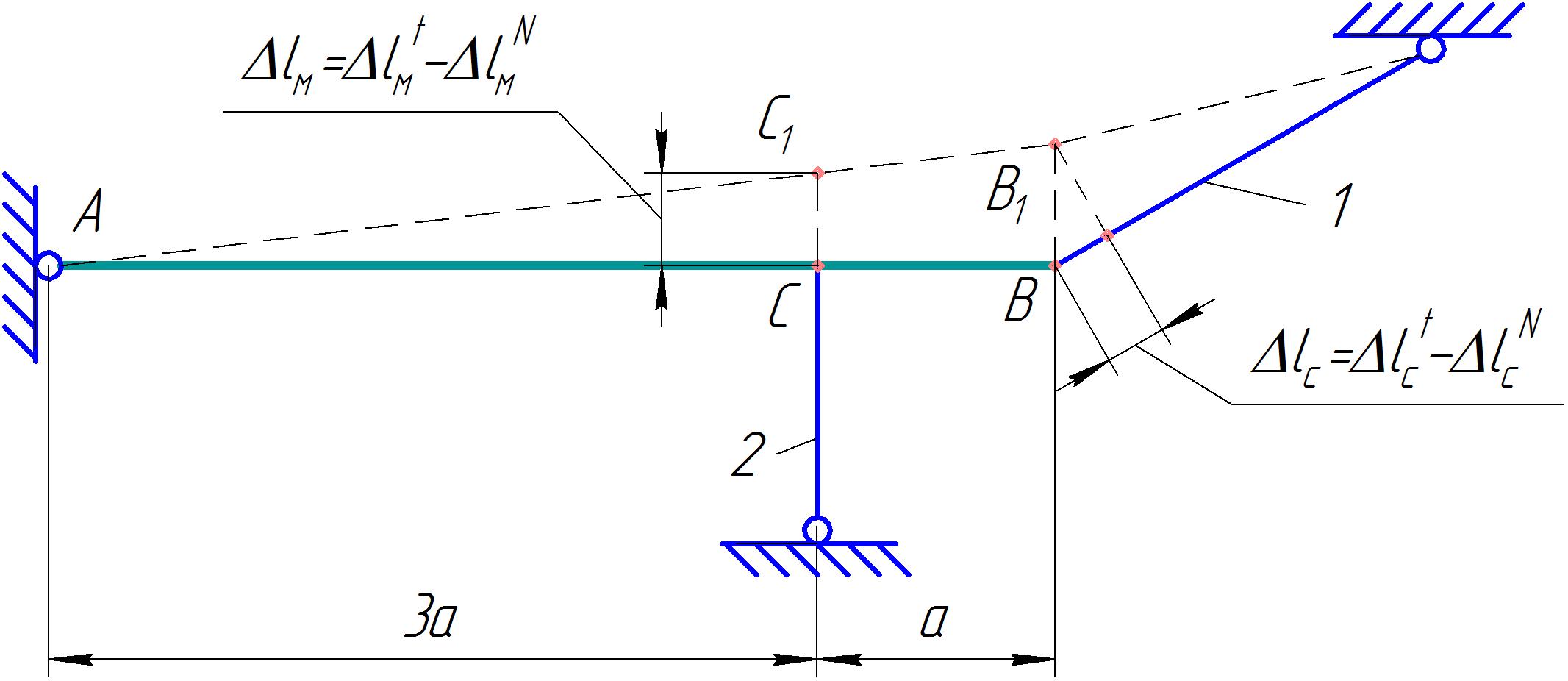 ак как коэффициент термического расширения меди больше, чем стали, то брус в конечном итоге переместится вниз, как показано на рисунке 5. И деформации медного и стального стержней будут иметь меньшие значения на величины Рис. 5 Направления внутренних температурных усилий в стержнях всегда согласованы со схемой деформаций стержней. Используем только одно уравнение равновесия статики: Уравнение совместности деформаций составим, рассматривая подобие треугольников АCC1и АВВ1: где Тогда Деформации в уравнении (7) выразим по закону Гука через усилия: 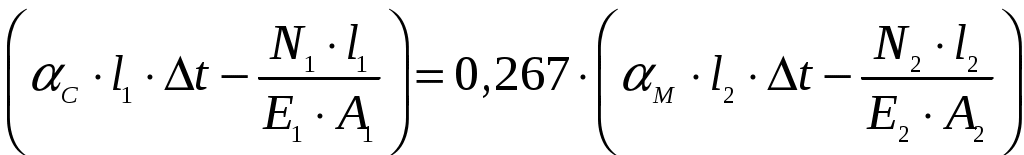 (8) (8)с учетом того, что 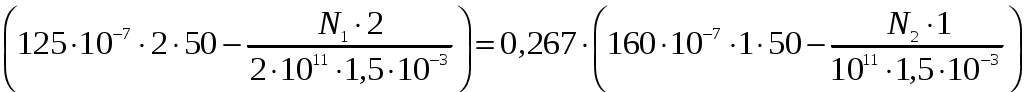 или после преобразований Подставляя этот результат в уравнение (6), находим температурное усилие в стержне 2: Усилие в стержне 1: Температурные напряжения в стержнях: в стержне 1 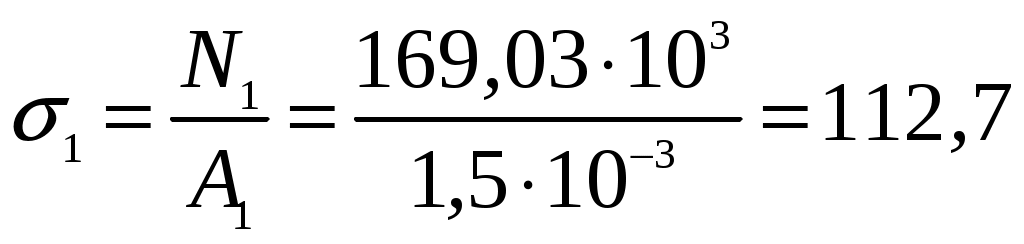 МПа; МПа;в стержне 2 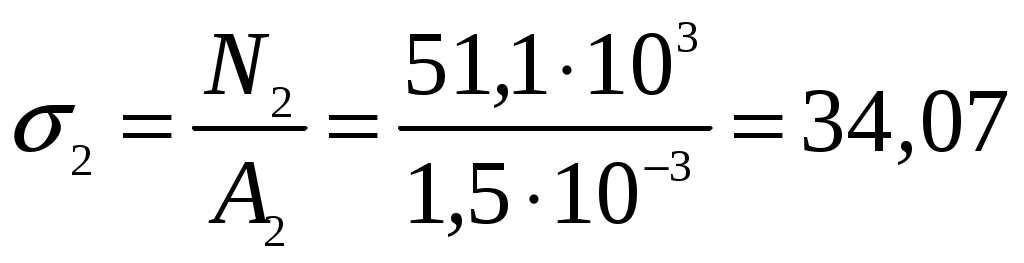 МПа. МПа. |
