определение нпгр. Определение нагрузок на головку балансира СК. Решение Определим параметр Коши , 8, стр. 50 (1)
 Скачать 32.76 Kb. Скачать 32.76 Kb.
|
|
2.2 Расчет оборудования 2.2.1 Определение нагрузок на головку балансира СК Исходные данные: L = 1259 м - глубина скважины; hd = 1189 м - динамический уровень; Dпл = 32 мм - диаметр плунжера; Dтр = 60 мм - диаметр труб; dшт1 = 22 мм - диаметр штанг; L1 = 560 м (44%) - длина колонны штанг; dшт2 = 19 мм - диаметр штанг; L2 = 699 м (56%) - длина колонны штанг;  = 885 кг/м3 - плотность жидкости; = 885 кг/м3 - плотность жидкости; = 1,26 = 1,26 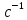 – угловая скорость вращения кривошипа; – угловая скорость вращения кривошипа;a = 4900 м/с – скорость звука в штангах; СК-12-2,5-4000 Решение Определим параметр Коши: µ =  , ,  [8, стр.50] (1) [8, стр.50] (1)µ = 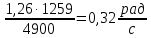 Максимальная нагрузка на СК по статической теории (формула Муравьева И.М.): 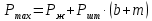 , ,  [8, стр.50] (2) [8, стр.50] (2)где Рж - вес столба жидкости, H; b - коэффициент облегчения штанг в жидкости; m - фактор динамичности. 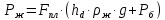 , , 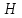 [8, стр.50] (3) [8, стр.50] (3)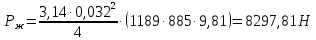 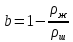 [8, стр.50] (4) [8, стр.50] (4)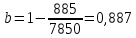 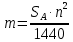 [8, стр.50] (5) [8, стр.50] (5)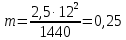 где SA - длина хода точки подвеса штанг= 2,5 м; n - число качаний в минуту=12  Вес штанг в воздухе, H: 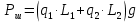 , , 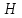 [8, стр.50] (6) [8, стр.50] (6) 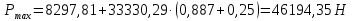 Минимальная нагрузка будет, очевидно, при начале хода штанг вниз, когда вес жидкости не действует на штанги, а динамический фактор вычитается: 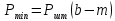 , , 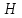 [8, стр.51] (7) [8, стр.51] (7)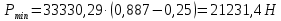 Определение нагрузок по формулам А.С. Вирновского:  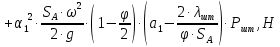 [8, стр.51] (8) [8, стр.51] (8)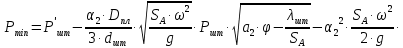 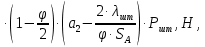 [8, стр.51] (9) [8, стр.51] (9)где 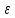 - отношение площадей просвета; - отношение площадей просвета;шт - удлинение штанг, м; P’ж - вес столба жидкости в кольцевом пространстве, H; P’шт - вес колонны штанг в жидкости, H; φ – коэффициент отношения площадей;  – кинематические коэффициенты. – кинематические коэффициенты.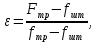 [8, стр.52] (10) [8, стр.52] (10)где  – площадь сечения внутреннего канала труб; – площадь сечения внутреннего канала труб;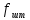 - площадь поперечного сечения штанг; - площадь поперечного сечения штанг;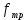 – площадь сечения труб по металлу. – площадь сечения труб по металлу.Расчет ведется для ступенчатой колонны штанг, поэтому вместо 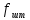 берем берем 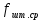 : : , , 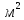 [8, стр.52] (11) [8, стр.52] (11)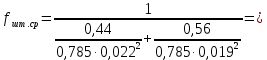 3,2∙ 3,2∙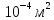 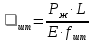 , м [8, стр.52] (12) , м [8, стр.52] (12)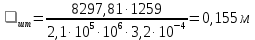 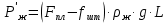 [8, стр.51] (13) [8, стр.51] (13)  [8, стр.51] (14) [8, стр.51] (14) 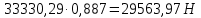 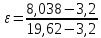 = 0,29 = 0,29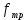 = 0,785 ( = 0,785 (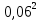 - -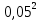 )=8,64∙ )=8,64∙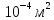 φ=  [8, стр.52] (15) [8, стр.52] (15)φ= 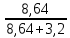 =0,729 =0,729Для СК-12-2,5-4000 при SA =2,5м 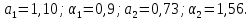  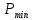 = = 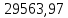 - - 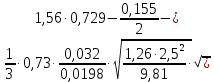 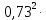 ∙∙ ∙∙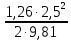 ∙ ∙  ∙ ∙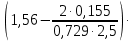 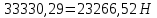 Упрощенные формулы А.С. Вирновского:  [8, стр.52] (16)  ∙ ∙ ∙ ∙ 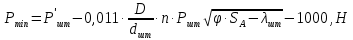 [8, стр.52] (17) 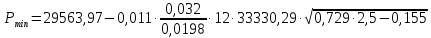 – – 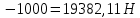 Максимальная нагрузка на основе динамической теории по формуле И.А. Чарного: 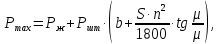 [8, стр.52] (18) [8, стр.52] (18)где 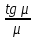 - коэффициент, учитывающий вибрацию штанг; - коэффициент, учитывающий вибрацию штанг;µ = 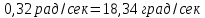 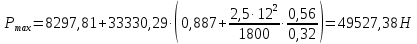 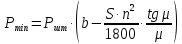 [8, стр.53] (19) [8, стр.53] (19)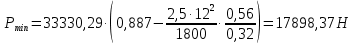 Максимальная нагрузка на основе динамической теории по эмпирической формуле А.Н. Адонина: 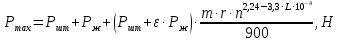 [8, стр.53] (20) [8, стр.53] (20)где m - кинетический коэффициент; 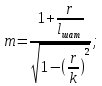 [8, стр.53](21) [8, стр.53](21)где 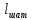 - длина шатуна; - длина шатуна;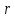 – радиус кривошипа; – радиус кривошипа;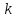 – длина заднего плеча балансира. – длина заднего плеча балансира. 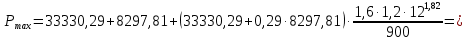 = 48647,22 H Таким образом, принимая за основу нагрузку, рассчитанную по формулам А.С. Вирновского, можно считать, что наиболее близкие значения по Pmax дают формула А.Н. Адонина 48647,22 H) и упрощенная формула А.С. Вирновского 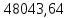 H; по Pmin наиболее близкие значения дают упрощенная формула А.С. Вирновского H; по Pmin наиболее близкие значения дают упрощенная формула А.С. Вирновского 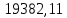 H и формула И.М. Муравьева H и формула И.М. Муравьева 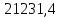 H. H.Оценивая трудоемкость расчетов, следует отметить, что для оценочных, приближенных расчетов Pmax следует пользоваться формулой И.М. Муравьева и уточненной автором для Pmin формулой, а для конструкторских или точных технологических расчетов следует пользоваться формулами А.С. Вирновского или А.Н. Адонина. |
