Решение Песчаные грунты а Наименование по гранулометрическому составу
 Скачать 0.64 Mb.
|
|
Задача №1 Определить физико-механические характкристики песчаного и глинистого грунтов. Дать их строительную классификацию. Определить условные расчетные сопротивления. Дано: Для песчаных грунтов: гранулометрический состав:  2,01 т/м3 10-2 мм – 5%, 2-0,5 мм - 25 2,65 т/м3 0,-0,25 мм – 15%, 0,25-0,1 мм – 13% 21,12 менее 0,1 мм- 18Для глинистых грунтов: 1,47 2,70 т/м3 20,01% 40,9% 25,4%Решение: 1.Песчаные грунты а) Наименование по гранулометрическому составу: т.к. вес частиц крупнее 0,1 составляет более 70% по массе, то песок является мелким. б) Коэффициент плотности: в= 2,65/2,01*(1+0,22)-1=0,61 т.к. е=0,61, то песок средней плотности. в) Степень влажности: S=0,22*2,65/0,61*1=0,81 т.е. песок насыщен водой. Вывод: Песок мелкий, средней плотности, насыщенный водой с=2 кПа, φ=32º, Е=28 МПа, R0=200 кПа. 2. Глинистые грунты а) Число пластичности: Ip=WL-Wp= 44,3-25,4=16,1% - супесь б) Показатель текучести: (24,4-25,4)/16,1 IL=(W-Wp)/Ip=(24,4-25,4)/16,1=0,23 – пластичная в) Коэффициент плотности: в= 2,71/1,47*(1+1,024)=1,95  т.е супесь влажная. Вывод: Супесь пластичная, влажная. с=14,8 кПа, φ=26º, Е=23,8 МПа, R0=275 кПа. Задача №2 Определить вертикальные сжимающие напряжения Gz от действия сосредоточенных сил Р1 и Р2, приложенных к поверхности массива грунта в точках, расположенных на оси Z по линии действия силы Р1. Определить сжимающие напряжения для точек на глубине Н. Построить эпюры напряжений от действия каждой силы и суммарные на одной схеме. Дано: Р1=2100 Р2= 2100 Н=2 м L=3 м Решение 1.а) Определяем Gz от Р1 по линии действия Р1 кi.1=0,4775 по табл. т.к.        б) Находим Gz от Р2 к1.2=0,0015·  к2.2=0,0251·  к3.2=0,0844·  к4.2=0,1565·  к5.2=0,2214·  к6.2=0,2733·  в) Находим суммарное Gz от Р1 и Р2 по оси z 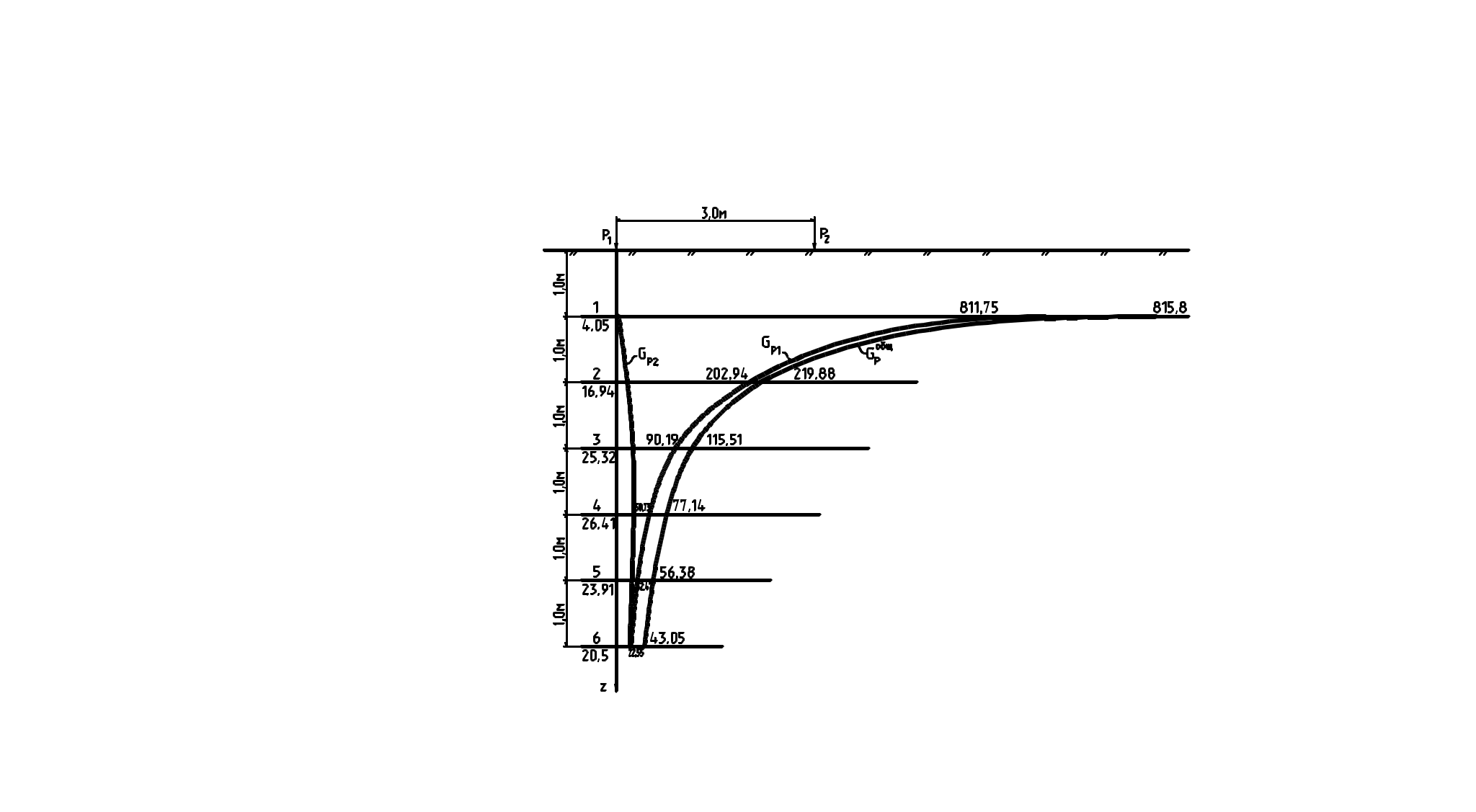       2. Определяем Gz для горизонтальной площадки на глубине Н а) Определяем Gz от Р1 по линии действия Р1 к7.1=0,0251·  к8.1=0,0844·   к9.1=0,2733·   к2.1=0,4775·  к10.1=0,2733·  к11.1=0,0844·  к12.1=0,0251·  б) Определяем Gz от Р2 по линии действия Р2 к7.2=0,0015·   к8.2=0,0034·   к9.2=0,085·   к2.2=0,0251·   к10.2=0,0844·  к11.2=0,2733·   к12.2=0,4775·   в) Находим суммарное Gz 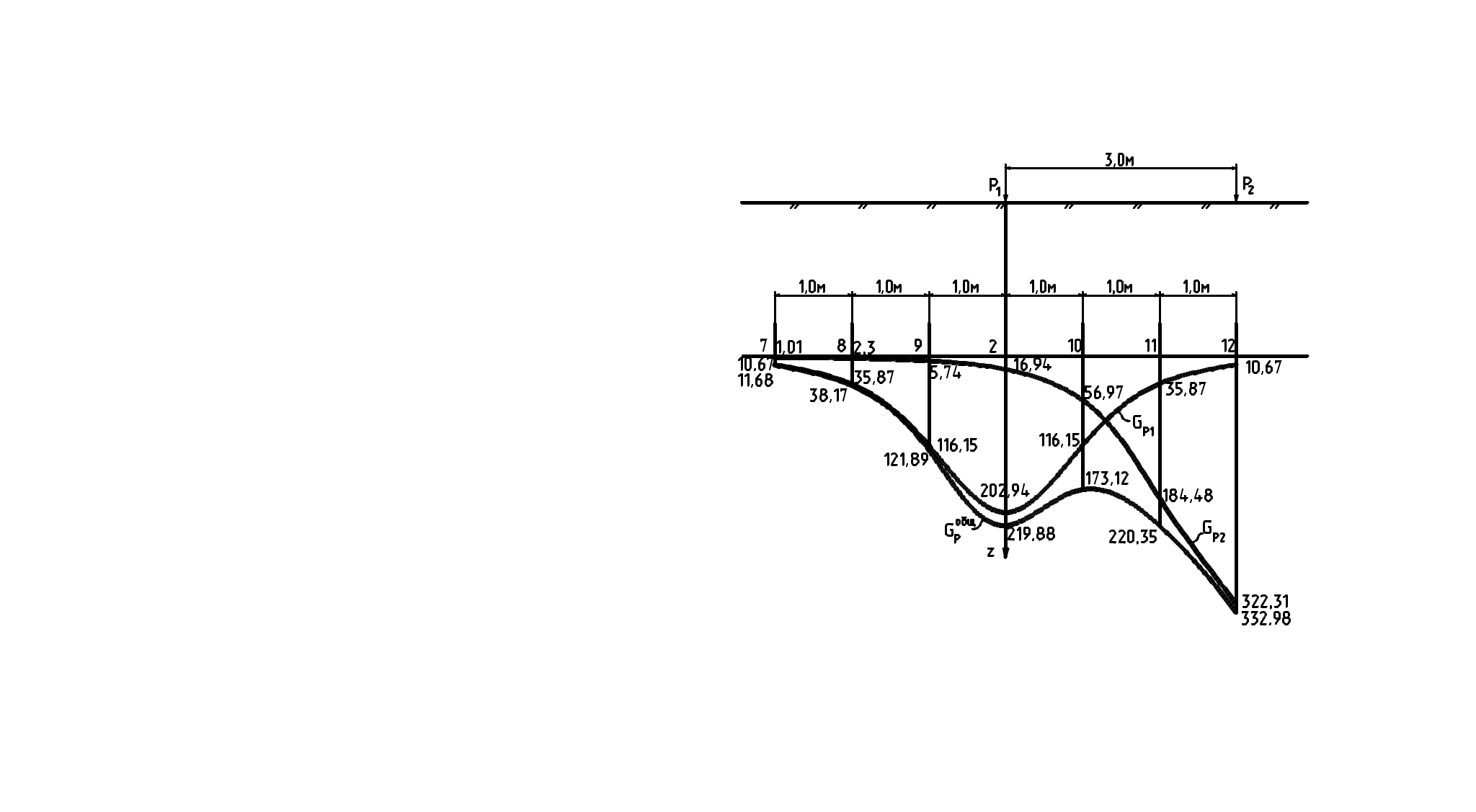       Задача №3 Определить методом послойного суммирования вероятную осадку «S» фундамента под колонну многоэтажного промышленного здания с полным каркасом и сравнить ее с предельной «Su». Грунт основания фундамента однородный на всю глубину. Дано: b=2,5 м l=2,5 м d=1,5 м Рср=0,40 МПа γ=19,5 кН/м3 Е=22 МПа суглинок Решение Составляем таблицу для нахождения δр
Рдоп=Рср-Gzg(d)=300-19,2=280,8 кПа ННГСТ=4,11 м – из графика GНГСТ=16,98 кН/м2          Sобщ=β·ΣSi=0.8·0.0341=0.027=2.7 см Sобщ= 2.7 см < «Su»=8 см – условие выполняется 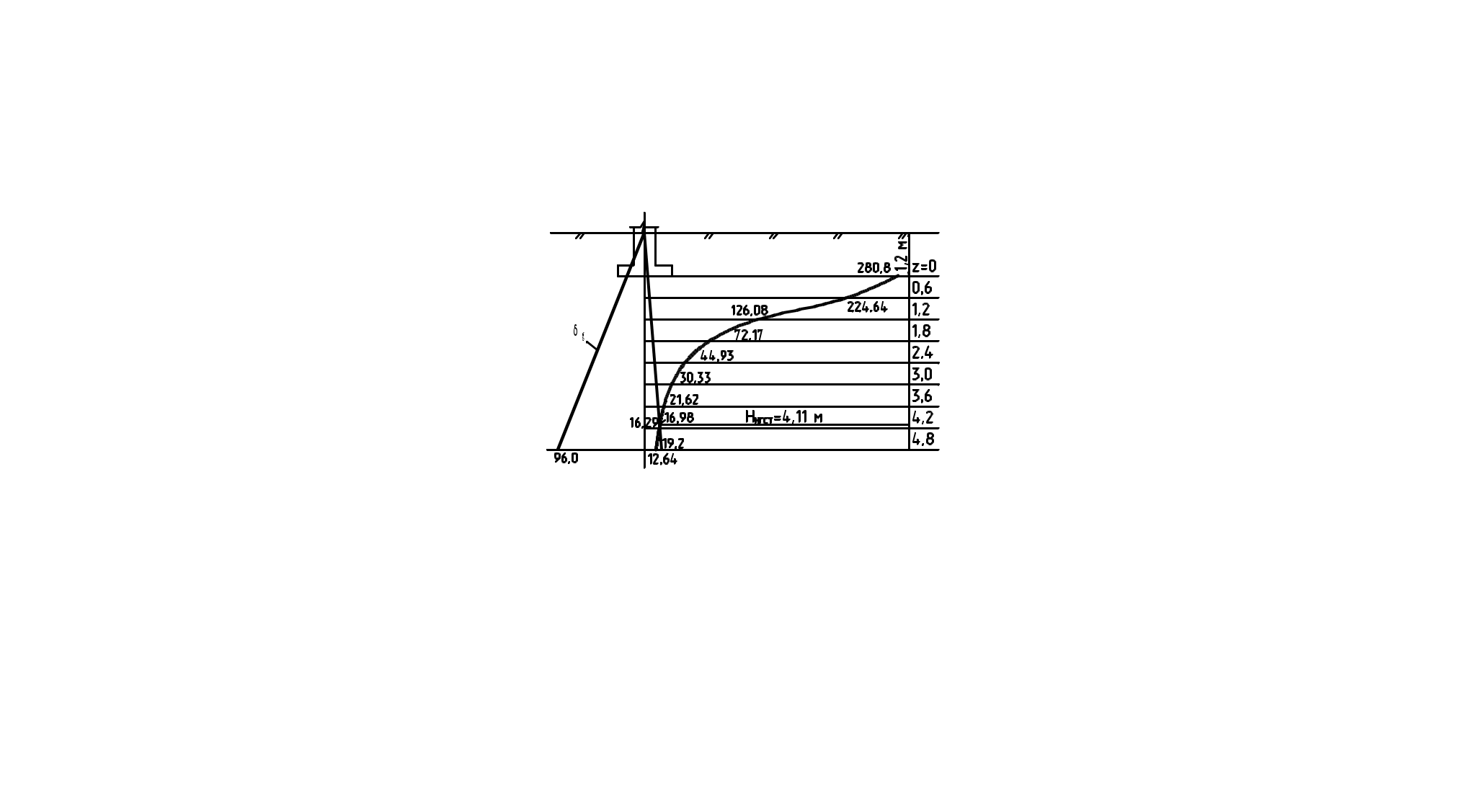 Задача №4 Определить устойчивость откоса методом круглоцилиндрических поверхностей скольжения. Положение центра и радиус наиболее опасной круглоцилиндрической поверхности определить с помощью диаграммы Ямбу. Дано: Н=100 м ρ=1,97т/м3 ρ=2,79т/м3 с=28 кПа φ=15º β=42º глина Решение   где γ=ρ·g=1,9·0,98=1,86 т/м3   и угол откоса β=45ºПо графику Ямбу находим значения х0=0,42 и у0=1,46 Тогда координаты центра вращения «0», будут равны: х=х0·Н=0,42·12=5,04 у=у0·Н=1,46·12=17,52 Из найденного центра вращения проводим окружность. Радиус дуги скольжения:  Разбиваем оползневое тело на блоки, графически определяем их ширину и высоту сторон. Составляем таблицу для расчета всех необходимых элементов, входящих в формулу 
Σ=109,01 Σ=244,1 Определяем длину дуги скольжения  sin β1=  =0.7 β1=44ºβ2= β1=44º β= β1+ β2=88º   т.к Кзап=4,5, что больше чем 1, то откос устойчив.                  |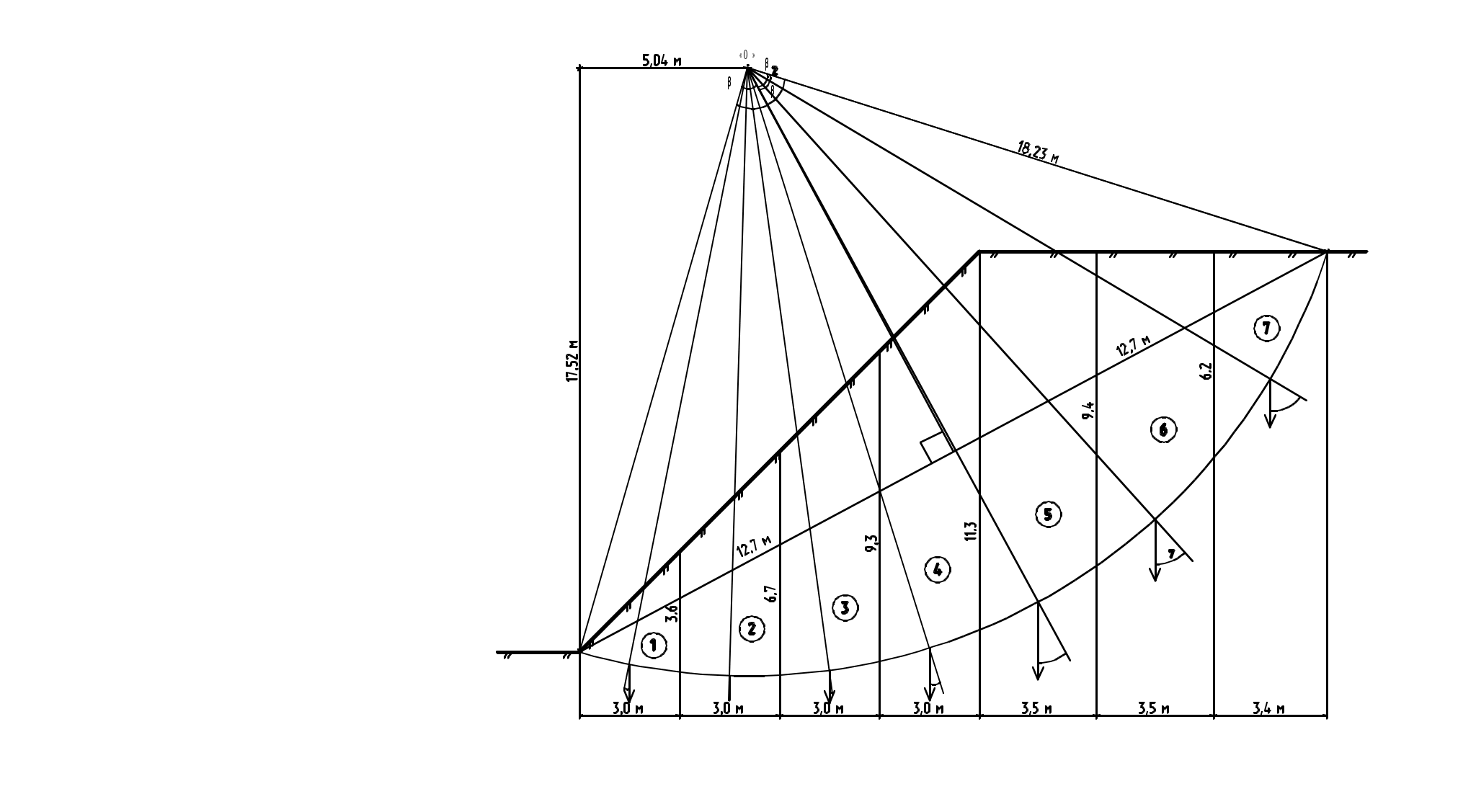
