РГР 1. Исследование функции напряжений. Решение плоской задачи теории упругости в напряжениях. Функция Эри. Полная система дифференциальных уравнений плоской задачи теории упругости имеет вид
 Скачать 88.94 Kb. Скачать 88.94 Kb.
|
|
1. Решение плоской задачи теории упругости в напряжениях. Функция Эри. Полная система дифференциальных уравнений плоской задачи теории упругости имеет вид: 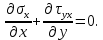 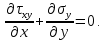 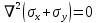 . .Это - простейшая из форм их записи, без учета распределенных объемных внешних сил (сил тяжести и инерционных сил), позволяющая представить уравнения как однородные (без правой части). Целесообразность записи основных уравнений в виде однородных, т.е. без правой части, заключается в том, что в таком случае система уравнений может быть сведена к одному параметрическому уравнению путем подстановки одной, разрешающей, функции (параметра). Это функция Эри, или функция напряжений. Действительно, если выразить три функции 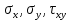 через одну функцию через одну функцию 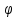 следующим образом (формулы Эри): 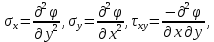 то первые два уравнения (уравнения равновесия) удовлетворяются тождественно (проверьте подстановкой). Третье уравнение (уравнение неразрывности и совместности перемещений) становится дифференциальным уравнением четвертого порядка 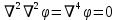 и является основным уравнением плоской задачи теории упругости в параметрической форме для случая решения задачи в напряжениях. В развернутом виде операторы Лапласа выглядят так: 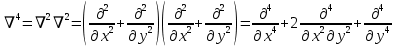 В механике все задачи в зависимости от их постановки разделяют на два типа. Если заданы внешние воздействия и требуется определить результат этих воздействий – прямая задача. Если же известны результаты некоего воздействия, а требуется восстановить, какого вида воздействие привело к таким результатам - обратная задача. Решение плоской задачи теории упругости в прямой постановке сводится к нахождению функции Эри, удовлетворяющей одновременно основному уравнению и граничным условиям. Затем по формулам Эри определяются напряжения. Если заданы внешние воздействия на контуре тела и требуется восстановить вид функции напряжений, то, согласно формулам Эри, придется прибегнуть к операции неопределенного интегрирования. (Для справки: определенный интеграл – число, неопределенный – функция). При интегрировании по каждому из двух переменных в качестве неопределенных компонент интеграла выступают не только числа (постоянные интегрирования), но также и неизвестного вида функции другого переменного. Это обстоятельство делает прямую задачу теории упругости неразрешимой в строго математическом смысле. На практике принято решать плоскую задачу теории упругости либо как обратную, подбирая соответствующего вида функции напряжений, либо приближенно,задаваясь видом неопределенных функций интегрирования. Рассмотрим первый из этих путей решения. Для начала проведем исследования элементарного вида функций напряжения на предмет их соответствия тем или иным граничным условиям. В дальнейшем этот опыт поможет нам конструировать сложные функции напряжения под заданные граничные условия. 2. Определение граничных условий по заданной функции напряжений. Пример 1. Имеем пластину прямоугольной формы постоянной толщины (Рис.1), нагружаемой по контуру внешними распределенными силами. Требуется восстановить характер распределения внешних сил (граничные условия), если функция напряжений имеет вид 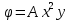 . .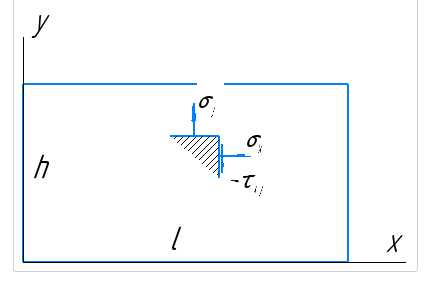 Рис.1 Согласно формулам Эри напряжения описываются формулами: 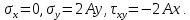 Непосредственно на поверхности пластины напряжения приобретают характер внешних распределенных по поверхности сил. На поверхность x=l выходят, т.е. отличны от нуля, напряжения 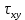 , становясь внешними граничными силами: , становясь внешними граничными силами: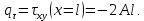 По закону парности касательных напряжений такими же, только противоположного знака, будут касательные нагружения на поверхностях y=0 при x=l и y=h при x=l. (Рис.2) 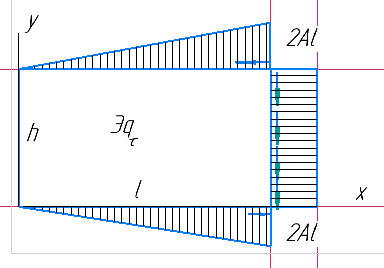 Рис. 2 На поверхность y=h напряжения 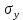 выходят уже в другом качестве – как внешние распределенные силы выходят уже в другом качестве – как внешние распределенные силы 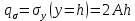 (Рис.3): (Рис.3):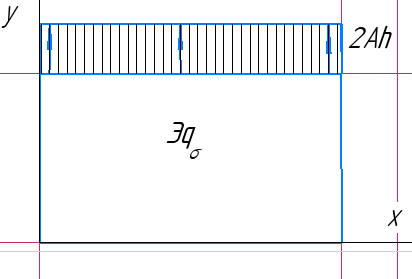 Рис. 3 Пример 2. Определить граничные условия прямоугольной пластины, напряженное состояние которой соответствует функции напряжений 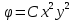 в системе координат, показанной на Рис.4. в системе координат, показанной на Рис.4.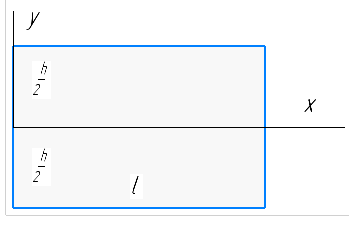 Рис.4 Определяем напряжения по формулам Эри: 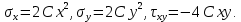 Нормальные напряжения 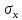 меняются только по координате x по закону квадратичной параболы (Рис.5), а непосредственно на правом контуре уравновешиваются внешней распределенной по этому контуру нагрузкой меняются только по координате x по закону квадратичной параболы (Рис.5), а непосредственно на правом контуре уравновешиваются внешней распределенной по этому контуру нагрузкой 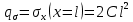 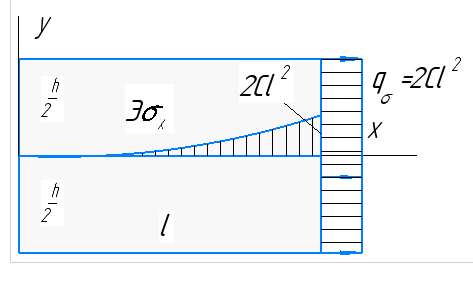 Рис.5 Нормальные напряжения 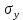 меняются только по координате y по закону квадратичной параболы (Рис.6) и приобретают на верхнем и нижнем контурах значение внешней распределенной по контуру нагрузки меняются только по координате y по закону квадратичной параболы (Рис.6) и приобретают на верхнем и нижнем контурах значение внешней распределенной по контуру нагрузки 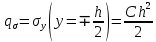 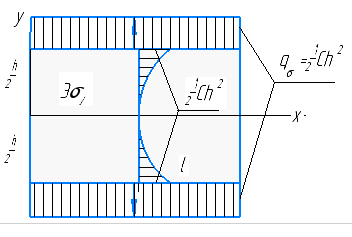 Рис.6 Касательные напряжения имеют линейный характер распределения как по сечениям, так и на контурах пластины (Рис.7): 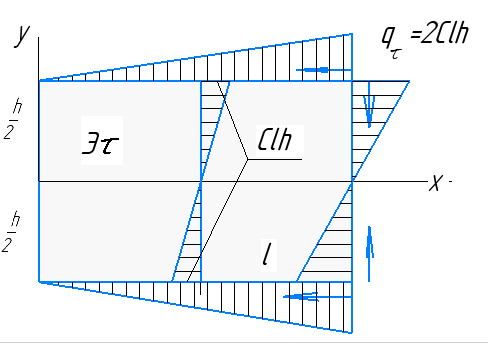 Рис.7 3. Проверка правильности определения внешних силовых факторов с помощью интегральных уравнений равновесия. В последнем примере сумма проекций всех внешних сил на ось x должна быть равна нулю: 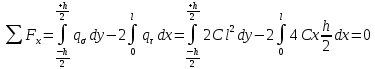 В простейшем случае, когда внешние силы распределены по поверхностям по линейным законам, операция интегрирования адекватна вычислениям площадей эпюров, представленных прямоугольниками либо треугольниками. В рассматриваемом случае площадь прямоугольника 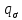 на Рис.5 должна быть равна сумме площадей двух горизонтальных треугольников на Рис.5 должна быть равна сумме площадей двух горизонтальных треугольников 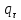 на Рис.7: на Рис.7: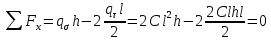 В проекции на ось y главные векторы контурных сил 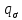 и и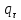 , как следует из рисунков, взаимно уравновешены. , как следует из рисунков, взаимно уравновешены.Взаимоуравновешенной в этом примере является также картина моментов контурных сил относительно начала координат, что также видно на рисунках. Однако в общем случае, либо при неудачном выборе точки определения моментов, необходимо составлять и решать интегральные уравнения. 4. Индивидуальные задания функции напряжений для исследования 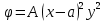 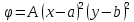 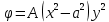 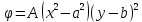 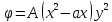 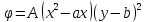 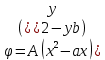 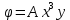 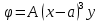 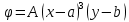 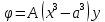 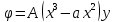 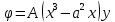 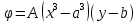 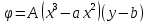 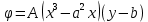 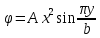 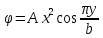 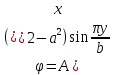 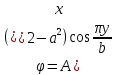 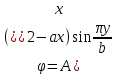 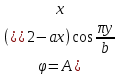 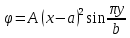 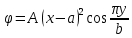 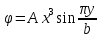 |
