Главная страница
Навигация по странице:

  • Задача

    		•

    Мат.статистика. Решение По несгруппированным данным найдем выборочную среднюю Найдем доверительный интервал


    Скачать 230 Kb.
    НазваниеРешение По несгруппированным данным найдем выборочную среднюю Найдем доверительный интервал
    Дата04.01.2022
    Размер230 Kb.
    Формат файлаdoc
    Имя файлаМат.статистика.doc
    ТипЗадача
    #323762

    Задача 1

    Требуется: 1) по несгруппированным данным найти выборочную среднюю; 2) найти доверительный интервал для оценки неизвестного математического ожидания признака X генеральной совокупности (генеральной средней), если признак X распределен по нормальному закону; известно  -надежность и  - среднее квадратическое отклонение; 3) составить интервальное распределение выборки с шагом h, взяв за начало первого интервала х0; 4) построить гистограмму частот; 5) дать экономическую интерпретацию полученных результатов.

    Получены результаты выборочного обследования по выполнении плана выработки на одного рабочего (в %):

    90,0; 96,0; 98,0; 98,0; 98,5; 99,0; 101,5; 102; 102; 102,5; 103; 103; 103,5; 104; 104; 104; 104,5; 105,5; 106; 108; 108,2; 108; 109; 112; 113,5.

    γ = 0,98; σ =4,7; h =5; x0 = 90.

    Решение:

    По несгруппированным данным найдем выборочную среднюю: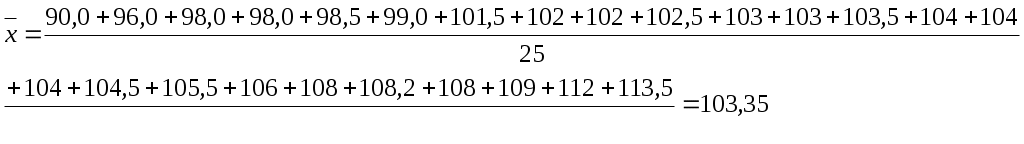

    Найдем доверительный интервал:





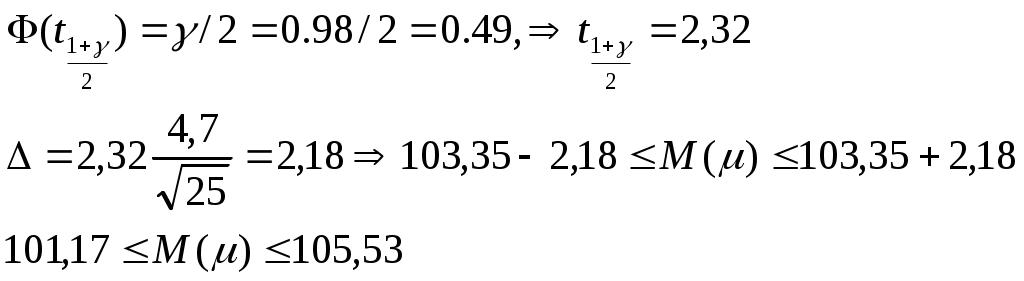    Интервальное статистическое распределение:

    х
    [90;95)
    [95;100)
    [100;105)
    [105;110)
    [110;115)

    пк
    1
    5
    11
    6
    2

    Построим полигон и гистограмму частот:



    10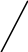












    5












    1

    х

    90 95 100 105 110 115

    Среднее выполнение плана выработки на одного рабочего составляет 103,35 %. Доверительный интервал означает, что с вероятностью, равной 0,98, можно утверждать, что среднее выполнение плана выработки на одного рабочего генеральной совокупности находятся в пределах от 101,17 % до 105,53 %.
    Задача 2

    По корреляционной таблице требуется: 1)в прямоугольной системе координат построить эмпирические ломаные регрессии Y на X и X на Y, сделать предположение о виде корреляционной связи; 2) оценить тесноту линейной корреляционной связи; 3) составить линейные уравнения регрессии Y на X и X на Y, построить их графики в одной системе координат; 4) используя полученное уравнение регрессии, оценить ожидаемое среднее значение признака Y при х=х0. Дать экономическую интерпретацию полученных результатов.

    В таблице дано распределение 100 предприятий по производственным средствам X в млн руб. и суточной выработки Y в т.:



    X

    Y
    20
    30
    40
    50
    60
    ny

    10
    8
    7
    2






    17

    20
    2
    16
    8
    6
    2
    34

    30



    9
    12
    12
    4
    37

    40






    2
    4
    5
    11

    50












    1
    1

    nх
    10
    32
    24
    22
    12
    n=100

    х=45.

    Решение:

    1) Для построения эмпирических ломаных регрессии вычислим условные средние.

    ; ;

    ; ;

    ;
    20
    30
    40
    50
    60



    12
    20,6
    25,8
    29,1
    34,2


    ; ; ; ; ;



    10
    20
    30
    40
    50



    26,5
    37,1
    43,0
    52,7
    60




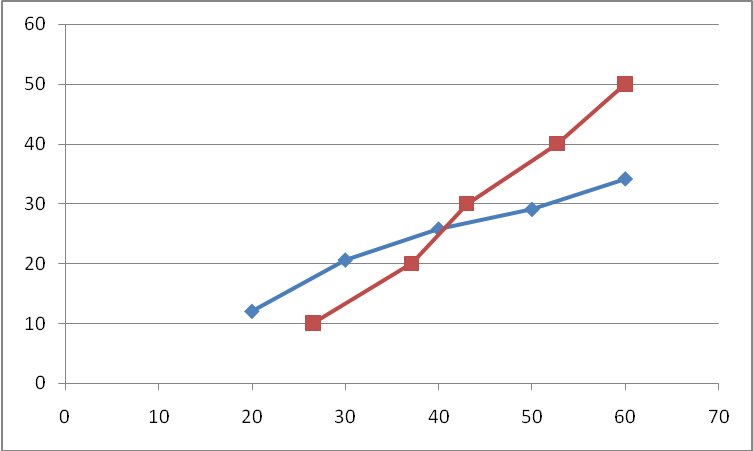    Можно выдвинуть гипотезу о прямой линейной корреляционной зависимости.

    2) Оценим тесноту связи. Вычислим выборочный коэффициент корреляции.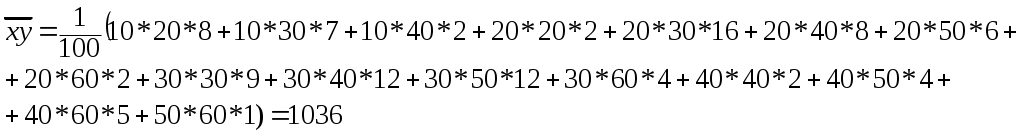

    , , ,

    , , ;

    , ;
    ;

    ;

    ;

    ;



    ;



    Это значение rB говорит о том, что линейная связь умеренная. Этот вывод подтверждает первоначальное предположение, сделанное исходя из графика.

    3) Запишем уравнения регрессии:

    , .

    Подставляя в эти уравнения найденные величины, получаем искомые уравнения регрессии:

    1) уравнение регрессии Y на X:

    , или ;

    2) уравнение регрессии X на Y: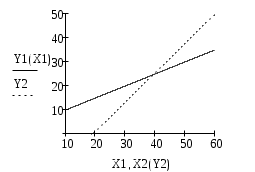

    , или


    Контроль: точка пересечения прямых линий регрессии имеет координаты . В нашем примере: С(39,4; 24,5).

    4) Найдем среднее значение Y при х=45 используя уравнение регрессии Y на X. Подставим в это уравнение х=45, получим



    Задача3

    Требуется: 1) выдвинуть гипотезу о виде распределения; 2)проверить гипотезу с помощью критерия Пирсона при заданном уровне значимости  = 0.05. За значения параметров а и  принять среднюю выборочную и выборочное среднее квадратичное отклонение, вычисленные по эмпирическим данным.

    3-4
    4-5
    5-6
    6-7
    7-8



    5
    11
    13
    12
    9

    Решение:

    Можно сделать предположение о нормальном распределении генеральной совокупности.

    Проверим выдвинутую гипотезу о нормальном распределении, используя критерий согласия Пирсона.

    Вычисляем , В.В качестве вариант возьмем среднее арифметическое концов интервалов:

    ;

    .

    i
    Граница интервалов
    Ф(Zi)
    Ф(Zi+1)
    Pi= Ф(Zi+1)-Ф(Zi)


    xi
    xi+1
    Zi
    Zi+1

    1
    3
    4
    -1,73
    -0,94
    -0,4582
    -0,3264
    0,1318
    7,249

    2
    4
    5
    -0,94
    -0,16
    -0,3264
    -0,0636
    0,2628
    14,454

    3
    5
    6
    -0,16
    0,63
    -0,0636
    0,2357
    0,2993
    16,4615

    4
    6
    7
    0,63
    1,42
    0,2357
    0,4222
    0,1865
    10,2575

    5
    7
    8
    1,42
    2,20
    0,4222
    0,4861
    0,0639
    3,5145

    Сравним эмпирические и теоретические частоты. Для этого:

    а) вычислим наблюдаемое значение критерия Пирсона.

    . Вычисления представлены в табл.6.

    i










    1
    5
    7,249
    -2,249
    5,058
    0,698

    2
    11
    14,454
    -3,454
    11,930
    0,825

    3
    13
    16,4615
    -3,4615
    11,982
    0,728

    4
    12
    10,2575
    1,7425
    3,036
    0,296

    5
    9
    3,5145
    5,4855
    30,091
    8,562



    б) найдем число степеней свободы R=S-2=5-2=3.

    По таблице критических точек распределения 2, по уровню значимости =0,05 и числу степеней свободы R=2 находим критическую точку .



    Сравниваем c . . Следовательно, есть основания отвергнуть гипотезу о нормальном распределении генеральной совокупности. Т.е. расхождение между эмпирическими и теоретическими частотами значимо.

    написать администратору сайта