Решение По всем четырем направлениям произведем расчеты по опред. Решение По всем четырем направлениям произведем расчеты по определению время нахождения транспорта на сегменте маршрута
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Задача 5 Для сопоставления рабочей загруженности нескольких предприятий связи создается модель. Количественное (численное) исследование модели позволяет установить поток исполненных услуг: принятых почтовых переводов (a), выданных почтовых переводов (b), приобретенных конвертов (c) и открыток (d), выданных бандеролей e) и т.д. Каждая процедура, рассматриваемая как отдельная услуга, характеризуется численным показателем. Набор численных показателей в течение 8 часов работы предприятия связи (период исследования) создавался для трех предприятий. Исходные данные: у – период исследования х1 – число принятых почтовых переводов
у – период исследования х2 – число выданных почтовых переводов
у – период исследования х3 – число приобретенных конвертов
у – период исследования х4 – число приобретенных открыток.
у – период исследования х5 – число выданных бандеролей.
Решение По каждой услуге в отделении почтовой связи, определим коэффициент корреляции между тремя моделями предприятия. Первая услуга – принятие почтовых переводов у – период исследования х1 – число принятых почтовых переводов
Коэффициент корреляции По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит: tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405 |tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым Вторая услуга – выдача почтовых переводов у – период исследования х2 – число выданных почтовых переводов
Коэффициент корреляции По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит: По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405 tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым Третья услуга – приобретение конвертов у – период исследования х3 – число приобретенных конвертов
Коэффициент корреляции По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит: tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405 tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым Четвертая услуга – приобретение открыток у – период исследования х4 – число приобретенных открыток.
Коэффициент корреляции По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит: tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405 tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым Пятая услуга – выдача бандеролей. у – период исследования х5 – число выданных бандеролей.
Коэффициент корреляции По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит: tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405 tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым Составляем итоговую таблицу по расчетам коэффициента корреляции по каждой услуге: 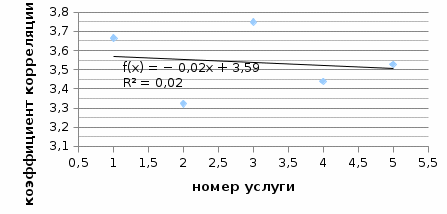 Рисунок 1 – Связь коэффициента корреляции от вида услуг Связь коэффициентов корреляции между предприятиями с учетом вида услуг – линейная, обратно пропорциональная. |
