Решение По всем четырем направлениям произведем расчеты по опред. Решение По всем четырем направлениям произведем расчеты по определению время нахождения транспорта на сегменте маршрута
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Задача 8 Имеет набор систем, таких, что кластер характеризуется функцией выхода:
Найти: функция выхода:
С учетом данных и наложенных условий по заданию функция выхода примет следующий вид: 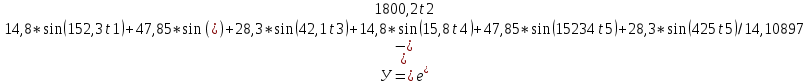 Проведем кластерный анализ. В качестве расстояния между объектами примем обычное евклидовое расстояние: где l - признаки; k - количество признаков Составляем матрицу расстояний: 
Минимизация расстояний: объекты 3 и 4 наиболее близки P3;4 = 29.56 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №3 и №4. В результате имеем 5 кластеров: S(1), S(2), S(3,4), S(5), S(6) Из матрицы расстояний следует, что объекты 1 и 3,4 наиболее близки P1;3,4 = 111.02 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1 и №3,4. В результате имеем 4 кластера: S(1,3,4), S(2), S(5), S(6) Из матрицы расстояний следует, что объекты 1,3,4 и 6 наиболее близки P1,3,4;6 = 273.03 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,3,4 и №6. В результате имеем 3 кластера: S(1,3,4,6), S(2), S(5) Из матрицы расстояний следует, что объекты 1,3,4,6 и 2 наиболее близки P1,3,4,6;2 = 1375.34 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,3,4,6 и №2. В результате имеем 2 кластера: S(1,3,4,6,2), S(5)
Таким образом, при проведении кластерного анализа получили два кластера, расстояние между которыми равно P=13433.8 Графическое представление кластера: 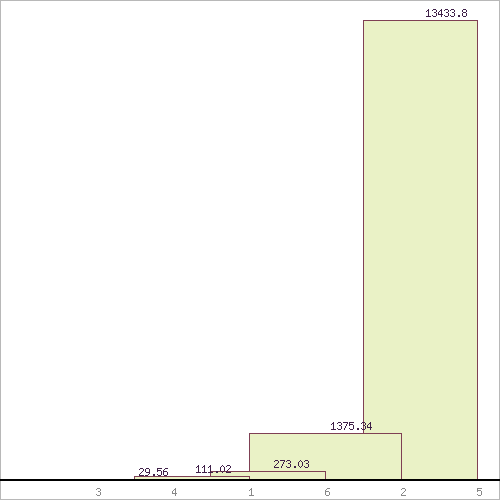 Задача 9 Имеется система информационных ресурсов (Серверов), представленная набором подсистем, взаимная связь которых характеризуется матрицей Структура системы:  Взаимная связь подсистем:  Рабочая нагрузка на каждую подсистему оценивается следующим образом:  Установить параметры системы согласно исходных данных:  Необходимо: -построить граф системы; вычислить частный и обобщенный показатель нагрузки (Уоб). Решение Частные показатели нагрузки: у1(t)=447,5/12,4*(sin(cos 4223,92)*0,1*2= -0,75786 у2(t)=447,5/12,4*(sin(cos 4223,92)*0,1*3= -1,13679 у3(t)=447,5/12,4*(sin(cos 4223,92)*0,1*2= -0,75786 у4(t)=447,5/12,4*(sin(cos 4223,92)*0,1*3= -1,13679 у5(t)=447,5/12,4*(sin(cos 4223,92)*0,1*1= -0,37893 у6(t)=447,5/12,4*(sin(cos 4223,92)*0,1*0= 0 у7(t)=447,5/12,4*(sin(cos 4223,92)*0,1*3= -1,13679 у8(t)=447,5/12,4*(sin(cos 4223,92)*0,1*1= -0,37893 Обобщенный показатель нагрузки: Уоб= 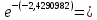 11,161415 11,161415    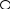   2   4 8 4 8        3 7 3 7   5 6 5 6 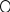 1 Граф системы Задача 10 Имеется система информационных ресурсов (Серверов), представленная набором подсистем, взаимная связь которых характеризуется матрицей:  Взаимная связь подсистем  Исходные данные:
Необходимо: -построить граф системы; вычислить частный и обобщенный показатель нагрузки (Уоб); - сравнить с результатами задачи 9. Решение Частные показатели нагрузки: у1(t)=71,5/0,17*(sin(cos 11775,44)*0,1*2= -0,5536119 у2(t)=71,5/0,17*(sin(cos 11775,44)*0,1*3= -0,8304178 у3(t)=71,5/0,17*(sin(cos 11775,44)*0,1*2= -0,5536119 у4(t)= 71,5/0,17*(sin(cos 11775,44)*0,1*3= -0,8304178 у5(t)=71,5/0,17*(sin(cos 11775,44)*0,1*1= -0,2768059 у6(t)=71,5/0,17*(sin(cos 11775,44)*0,1*0= 0 у7(t)= 71,5/0,17*(sin(cos 11775,44)*0,1*3= -0,8304178 у8(t)=71,5/0,17*(sin(cos 11775,44)*0,1*1= -0,2768059 Обобщенный показатель нагрузки: Уоб= 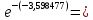 35,6658504 35,6658504         3 5 3 5   1 6 1 6  4 4   2 2   7  8 8Граф системы Сравнение результатов заданий 9 и 10: нагрузка системы задания 10 больше чем в три раза больше нагрузки системы задания 9. |




