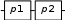Практическая работа 6. Проектный расчет надежности технической системы Цель
 Скачать 206.31 Kb. Скачать 206.31 Kb.
|
Практическая работа №6. Проектный расчет надежности технической системыЦель:
Задачи:
Основные теоретические сведения Техническая система состоит из большого числа подсистем, (элементов), имеющих между собой определенную взаимную связь. Для расчета надежности системы:
По принципу функционального назначения различают системы:
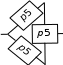
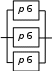
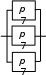
При последовательном соединении (рис. 1) вероятность безотказной работы системы определяется как произведение надежностей pi подсистем 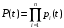 . (1) . (1) Рис. 1. Последовательное соединение Для экспоненциального закона распределения 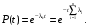 (2) (2)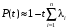 . (3) . (3)При параллельном соединении (рис. 2) вероятность безотказной работы системы определяется как 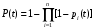 . (4) . (4)Для экспоненциального закона распределения 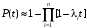 . (5) . (5)При смешанном соединении применяются различные схемы соединений, например, «два из трех», при которой система остается работоспособной, благодаря исправному состоянию любых двух элементов (рис. 3) P(t)=p3(t)+3p2(t)·q(t). (6) 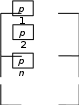 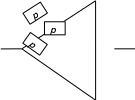 Рис. 2. Параллельное соединение Рис. 3. Соединение два из трех Вероятность безотказной работы системы в течение всего временного интервала определяется выражением вида P(t)=p1(t1)·p2(t2)·p3(t3)·… pn(tn), (7) где t1; t2,..., tn− интервалы времени, соответствующие вероятностям отказов подсистем p1, p2, ..., pn. Пример.В соответствии с техническим заданием разработана конструкторская документация на изделие типа подвижного транспорта. Требуется рассчитать вероятность безотказной работы и коэффициент готовности для трех элементов и всей системы при экспоненциальном законе распределения для структурной схемы надежности ТС (рис. 4).  Рис. 4. Структурная схема надежности ТС Данные для расчета:
Таблица 1 Таблица интенсивности отказов
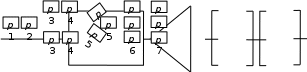 Рис. 5. Структурная схема надежности электроавтоматики Решение Расчет надежности элемента 1 Вероятность безотказной работы P1(t): 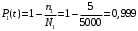 . .Для определения коэффициента готовности найдем среднюю наработку на отказ 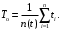 Примем наработку за указанный период: 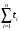 =N1·tц =5000·6=30000 ч. =N1·tц =5000·6=30000 ч.Наработка на отказ: 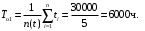 Коэффициента готовности: 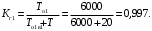 Расчет надежности элемента 2 Вероятность безотказной работы P2(t): 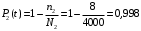 . .Примем наработку за указанный период: 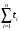 =N2·tц =4000·6=24000 ч. =N2·tц =4000·6=24000 ч.Наработка на отказ: 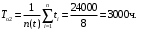 Коэффициента готовности: 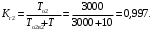 Расчет надежности элемента 3 Для расчета надежности элемента 3 представим структурную схему в виде пяти ветвей I, II, III, IVи V (рис. 6).
Рис. 6. Ветви структурной схемы: а – ветвь I (последовательное соединение); б – ветвь II (смешанное соединение – поканальное резервирование); в – ветвь III (соединение два из трех); г, д – ветвь IV, V(параллельное соединение – поэлементное резервирование) Ветвь I Надежность найдем по формулам (1, 3) 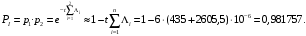 Ветвь II Надежность последовательных соединений найдем по формулам (1, 3) 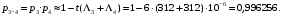 Надежность ветви (5) 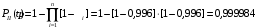 . .Ветвь III Для расчета воспользуемся формулами (3, 6): 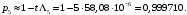 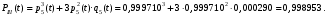 Ветви IV, V Для расчета воспользуемся формулами (1–3): 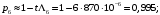 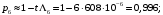 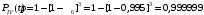 ; ;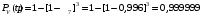 . .Надежность системы электроавтоматики (5) 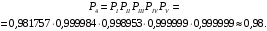 Коэффициент готовности: 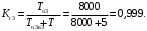 Надежность всей системы (рис. 5.) 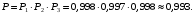 Коэффициент готовности всей системы 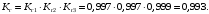 Задание Рассчитать вероятность безотказной работы и коэффициент готовности для трех элементов и всей системы при экспоненциальном законе распределения для структурной схемы надежности ТС (рис. 7). Данные для расчета элементов №1 и №2 представлены в таблице 4. Таблица 4 Данные по элементам №1 и №2
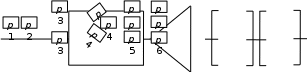 Рис. 7. Структурная схема надежности электроавтоматики Среднее время восстановления одного отказа составилоTв3=10 ч, среднее время наработки на отказ Tо3=10000 ч. Данные по интенсивности отказов сведены в таблицу 5. Таблица 5 Таблица интенсивности отказов
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||