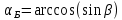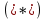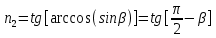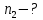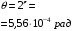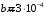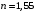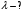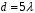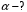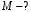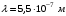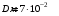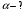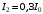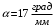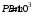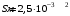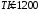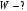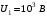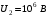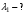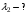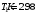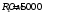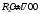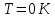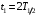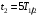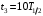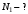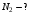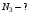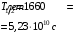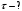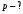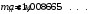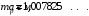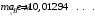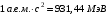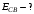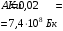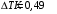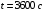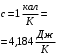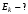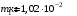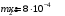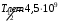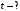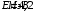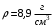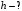РГЗ. Решение По закону Снелла где показатель преломления воздуха
 Скачать 391.68 Kb. Скачать 391.68 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования  «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра физики Отчёт по РГЗ: Выполнил: ст. группы МЦ-21-1 / Баканов А.В. / (должность) (подпись) (Ф.И.О) Проверил: доцент / Стоянова Т.В. / (должность) (подпись) (Ф.И.О) Вариант 2
Размерность: 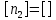 Вычисления: 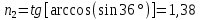 Ответ: 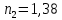 2.На тонкий стеклянный клин падает по нормали монохроматический свет. Преломляющий угол клина равен 2``. Показатель преломления стекла равен 1,55. Определить длину волны, если расстояние между соседними светлыми интерференционными полосами, равно 0,3 мм.
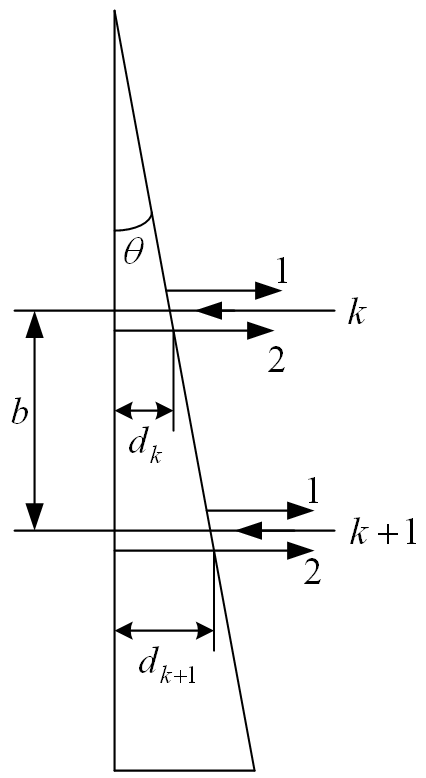 Условие минимума интерференции имеет вид: 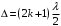 , где , где 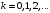 Разность хода лучей 1 и 2 равна: 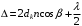 , где , где  - угол преломления пучка; - угол преломления пучка; 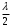 учитывает то, что пучок 1 отражается от более плотной среды и происходит изменение фазы на π. учитывает то, что пучок 1 отражается от более плотной среды и происходит изменение фазы на π.По закону преломления имеем: 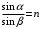 (учтено что падение из воздуха и его показатель преломления равен единице). (учтено что падение из воздуха и его показатель преломления равен единице).Принимаем что происходит нормальное падение на пленку, значит, 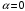 . .Значит, 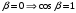 . .Тогда,  . .Значит, 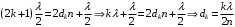 . .Для соседней полосы имеем: 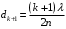 . .Из рисунка видно, что 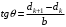 . .Значит, 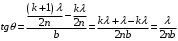 . .Тогда, 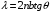 . .Получаем, 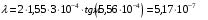 . .Ответ. 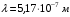 . .3.При заполнении находящейся на пути из интерферирующих лучей в интерферометре Жамена пустой трубки длиной 5 см кислородом (n=1.000272) происходит смещение интерференционных полос. Какую толщину должен иметь компенсирующий стеклянный клин (nст=1,5) на пути второго луча, чтобы восстановилась первоначальная картина?    Дано: l = 5 см 5·10-2 м nк =1,000272 nст =1,5 d - ?   Смещение картины произошло из-за того, что изменилось значение оптической разности хода 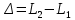 На участке, соответствующем длине трубки, оптический путь первого луча равен 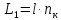 второго  Тогда, поскольку первоначальная картина восстановилась, имеем 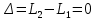 Поэтому 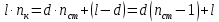 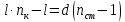 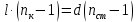 Определим толщину пластинки 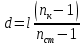 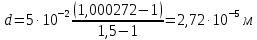 Ответ: 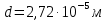 4.Постоянная дифракционной решетки в 5 раз больше длины световой волны монохроматического света нормально падающего на ее поверхность. Определить угол между двумя первыми дифракционными максимумами. Сколько максимумов наблюдается в спектре?
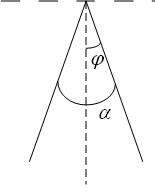 Для дифракционной решетки: 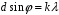 . .Так как 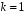 , значит , значит 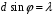 . .Значит,  . Тогда, . Тогда, 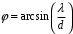 . .Из рисунка 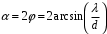 . .Получаем, 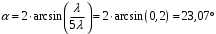 . .Наибольшее число дифракционных максимумом равно: 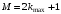 . . Уравнение дифракционной решетки: 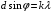 . .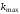 при при 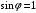 . Значит, . Значит, 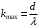 . Тогда, . Тогда, 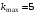 . .Значит,  . .Ответ. 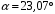 , ,  . .5.Две звезды рассматриваются в зрительную трубу. Угол между лучами, идущими от звезд к месту наблюдения – α. Наблюдение ведется через светофильтр пропускающий свет с длиной волны 550 нм. Определить при каком минимальном угле α, звезды можно будет наблюдать в зрительную трубу раздельно, если диаметр объектива зрительной трубы 70 мм.
 . .Получаем,  . .Ответ. 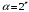 . .6.Естественный свет падает на систему из двух скрещенных николей, между которыми расположена кварцевая пластинка, вырезанная перпендикулярно оптической оси. Найти минимальную толщину пластинки, при которой система пропускает 0,3 светового потока, если постоянная вращения кварца 17 град/мм.
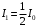 . .После второго николя имеем: 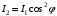 , где , где 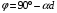 . .Значит, 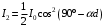 , ,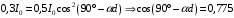 . .Тогда,  . . Значит, 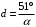 . .Получаем, 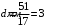 . .Ответ. 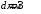 . .7.Муфельная печь потребляет мощность 1 кВт. Температура ее внутренней поверхности при открытом отверстии площадью 25 см2 равна 1,2 кК. Считая, что отверстие печи излучает как черное тело, определить, какая часть ее мощности рассеивается стенками.
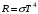 , где , где 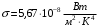 - постоянная Стефана-Больцмана. - постоянная Стефана-Больцмана.Мощность излучения равна: 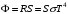 . .Значит, 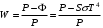 . .Получаем,  . .Рассеивается 70 % мощности. Ответ.  . .8.Найти длину волны де Бройля протона, прошедшего ускоряющую разность потенциалов: 1) 1 кВ; 2) 1 МВ.
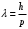 , где , где 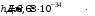 - постоянная Планка. - постоянная Планка.По закону сохранения энергии: 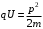 , где , где 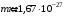 - масса протона, - масса протона, 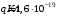 - заряд протона. - заряд протона.Тогда, 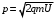 . Значит, . Значит, 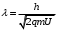 . .Тогда, 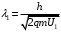 , , 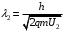 . .Проверка размерности: 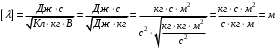 . .Получаем, 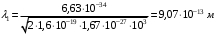 , ,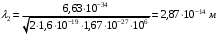 . .Ответ.  , , 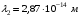 . .9.Определить ширину запрещенной зоны собственного (беспримесного) полупроводника, если при температуре 25ºС сопротивление 5000 Ом, а при 80ºС его сопротивление всего 700 Ом.
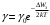 , где , где 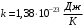 - постоянная Больцмана. - постоянная Больцмана.Значит, 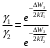 . .Так как 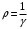 и и 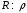 , то имеем: , то имеем: 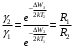 . .Значит, 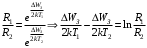 . .Тогда, 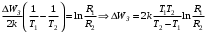 . .Проверка размерности: 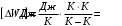 . .Получаем, 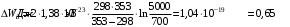 . .Ответ. 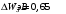 . .10.Определить концентрацию свободных электронов в металле при температуре 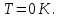 Энергию Ферми принять равной 1эВ. Энергию Ферми принять равной 1эВ.Дано:
Решение: Энергия уровня Ферми при Т=0К определяется формулой: 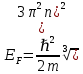 Где ℏ=1,05*10-34Дж*с – постоянная Планка m=9,1*10-31кг– масса электрона n – Концентрация электронов Имеем:  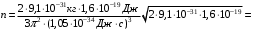 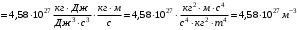 Ответ: 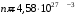 11.Какое количество радиоактивного элемента останется не распавшимся по истечении 2, 5, 10 периодов полураспада?
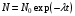 , где , где 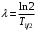 - постоянная распада. - постоянная распада.Значит, 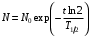 . .Тогда, 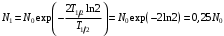 , ,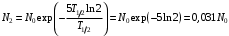 , ,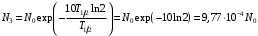 . .Ответ. 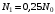 , , 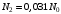 , , 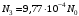 . .12.Период полураспада радия 226Ra составляет 1660 лет. Вычислить среднюю продолжительность жизни атомов радия и вероятность для одного атома распасться в течение 1 года.
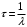 , где , где 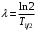 - постоянная распада. - постоянная распада. Значит, 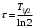 . .Вероятность распада равна:  . .Получаем, 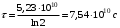 , , 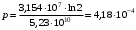 . . Ответ.  , , 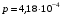 . .13.Определить энергию связи нуклонов в ядре изотопа бора 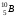 . Масса нейтрона 1,008665 а.е.м.; масса протона 1,007825 а.е.м.; массу ядра бора определить по справочным данным. . Масса нейтрона 1,008665 а.е.м.; масса протона 1,007825 а.е.м.; массу ядра бора определить по справочным данным.
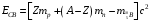 . .Имеем, 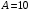 - массовое число, - массовое число, 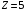 - зарядовое число. - зарядовое число.Значит, 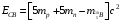 . .Получаем, 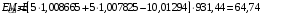 . .Ответ. 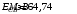 . .14.Вычислить энергию α-частицы, испускаемой изотопом радия 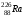 , если препарат радия активностью 0,02 Ки, помещенный в калориметр, вызывает повышение температуры на 0,49ºС в час. Теплоемкость калориметра 1 кал/ºС. , если препарат радия активностью 0,02 Ки, помещенный в калориметр, вызывает повышение температуры на 0,49ºС в час. Теплоемкость калориметра 1 кал/ºС.
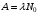 , где , где 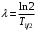 - постоянная распада, - постоянная распада, 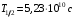 - период полураспада радия. - период полураспада радия.Тогда, 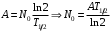 . .Энергия, которая идет на нагревание калориметра равна: 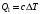 . .Энергия альфа-частиц, которые нагревают калориметр равна: 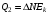 . .Число альфа-частиц равна числу распавшихся ядер:  . .Значит, 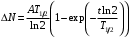 . .Так как 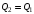 , то , то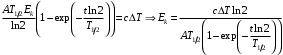 . .Проверка размерности: 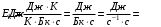 . .Получаем, 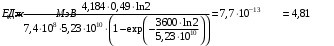 . .Ответ. 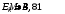 . .15.Анализ изотопного состава свинца некоторой горной породы показал, что на каждые 10,2 г изотопа урана 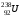 , содержащегося в породе, приходится 0,8 г радиогенного (т.е. образовавшегося за счет распада урана) изотопа свинца , содержащегося в породе, приходится 0,8 г радиогенного (т.е. образовавшегося за счет распада урана) изотопа свинца 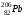 . Определить возраст этой горной породы. Период полураспада . Определить возраст этой горной породы. Период полураспада 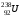 составляет 4,5·109 лет. составляет 4,5·109 лет.
Имеем, 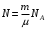 , где , где 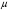 - молярная масса, - молярная масса, 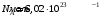 - число Авогадро. - число Авогадро.Для урана: 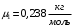 . .Для свинца: 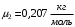 . .Значит, 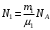 , , 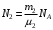 . .По закону радиоактивного распада: 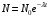 . . Тогда, число распавшихся ядер равно: 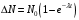 . .Значит, 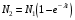 . .Постоянная радиоактивного распада: 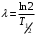 . .Тогда, 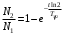 . .Значит,  . .Получаем, 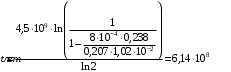 . .Ответ. 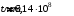 . .16.На какую глубину в пластинку, изготовленную из меди, проникает альфа-частица имеющая энергию 4,2 МэВ? Плотность меди 8,9 г/см3.
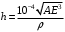 , где , где 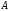 - атомная масса, - атомная масса, 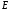 - энергия альфа-частицы в - энергия альфа-частицы в 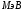 , , 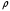 - плотность в - плотность в 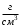 , , 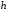 - максимальная глубина в - максимальная глубина в 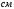 . .Атомная масса алюминия: 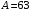 . .Получаем, 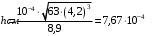 . .Ответ. 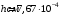 . . |

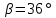
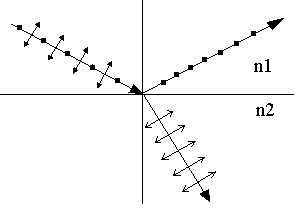
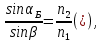 где
где 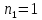 – показатель преломления воздуха.
– показатель преломления воздуха.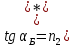
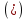 и
и 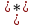 имеем:
имеем: 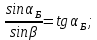
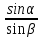 =
= 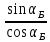 ;
; 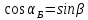 ;
;