ргр1. Решение. Подберём поперечные размеры сечения

• Название: Решение. Подберём поперечные размеры сечения
• Дата: 06.01.2022
• Размер: 163.28 Kb.
• Имя файла: ргр1.docx
• Тип: Решение; #325196

Задача 8

Дано : P=8 кН ; l=0.75 м ; Ст 3.

Требуется : 1. Подобрать поперечные размеры стержня при заданном допускаемом напряжении на сжатие [σ]=160 МПа ;

2. Найти величину критической силы и коэффициент запаса устойчивости [n_y] ;

3. Вычертить поперечное сечение стойки в масштабе 1:1.

4. Распечатать полученные результаты и приложить их к основному расчёту.

Решение.



1. Подберём поперечные размеры сечения.

Определим моменты инерции сечения относительно координатных осей x и y

J_x= =0.92a⁴

J_y=

Площадь сечения : F=2a×1.5a-a²=2a²

i_x= =0.68a

i_y= =0.49a

Определим гибкость первого приближения.

λ_max=μl/i_min=0.5×0.75/(0.49a)=0.77/a

Зададимся величиной a=0.005 м. Тогда значение гибкости первого приближения будет равно λ=154. Пользуясь таблицей 9 заданий на контрольные работы, будем иметь следующие значения для проведения линейной интерполяции :

при λ=140 ; φ=0.36

при λ=160 ; φ=0.29

С учётом этих данных для λ=154 , получим :

φ=0.29+ 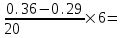0.31

Напряжение в поперечном сечении стержня : σ_p=

σ_p= =516×10⁶=516 МПа>[σ]=160 МПа.

Вычисления показывают, что стержень при данных размерах не устойчив.

В связи с этим сделаем второе приближение, увеличив размер а.

Зададим а=0.01 м. Тогда значение гибкости второго приближения будет равно :

λ=0.77/0.01=77.

Пользуясь таблицей 9 заданий на контрольные работы, будем иметь следующие значения для проведения линейной интерполяции :

при λ=80 ; φ=0.75

при λ=90 ; φ=0.69

С учётом этих данных для λ=77 , получим :

φ=0.69+ 0.71

Напряжение в поперечном сечении :

σ= =56.3×10⁶ Па=56.3 МПа<160 МПа

Вычисления подтверждают наличие устойчивого деформирования и отсутствия потери устойчивости при полученных размерах. Однако недонапряжение стойки в данном случае чрезмерное, поскольку :

и составляет 65%, что является недопустимым.

Зададим а=0.007 м. При этом значение гибкости третьего приближения будет равно :

λ=0.77/0.007=110. Воспользовавшись таб. 9, получим :

при λ=110 ; φ=0.52

Напряжение в поперечном сечении :

σ= =157×10⁶ Па=157 МПа<160 МПа

Проверяя возможное недонапряжение стойки, имеем :

, что составляет 1.9%, что допустимо.

2. Найдём величину критической силы и коэффициент запаса устойчивости [n_y].

По таблице 1 методических указаний, для материала Ст 3 λ_пред=100. Так как гибкость стержня λ=110>λ_пред, то для вычисления σ_кр следует использовать формулу Эйлера. Имеем :

σ_кр= =163 МПа

Площадь подобранного ранее сечения составляет F=2a² , а именно

F=2×0.007²=98×10^-6 м².

Очевидно, что критическая нагрузка в рассматриваемом примере будет равна :

P_кр=σ_крF=163×10³×98×10^-6=16 кН.

Поделив P_кр на P, получим искомую величину коэффициента запаса устойчивости :

[n_y]=P_кр/P=16/8=2