Дифференциальные уравнения. 3 ДУ однородные 1 пор. Решение Полагаем или . Тогда исходное уравнение примет вид Разделяем переменные . Интегрируем
 Скачать 51.95 Kb. Скачать 51.95 Kb.
|
|
Однородные уравнения Функция 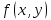 называется однородной функцией переменных называется однородной функцией переменных 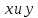 порядка m, если при любомt справедливо тождество порядка m, если при любомt справедливо тождество 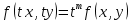 . . Дифференциальное уравнение M( 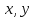 )dx+N( )dx+N(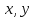 )dy=0 )dy=0называется однородным, если коэффициенты M( 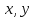 ) и N( ) и N(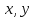 ) есть однородные функции одного того же порядка. Данное уравнение сводится к уравнению с разделяющимися переменными с помощью подстановки ) есть однородные функции одного того же порядка. Данное уравнение сводится к уравнению с разделяющимися переменными с помощью подстановки 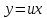 , где u – новая переменная. , где u – новая переменная.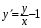 . .П 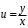 ример 1. Проинтегрировать ДУ: . ример 1. Проинтегрировать ДУ: .Решение: Полагаем или 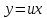 ⇒ ⇒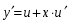 . .Тогда исходное уравнение примет вид: 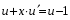 . .Разделяем переменные 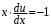 ⇒ ⇒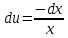 . .Интегрируем: 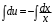 , ⇒ , ⇒ 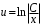 . . П 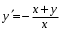 осле обратной замены получим общий интеграл осле обратной замены получим общий интеграл 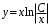 . .Пример 2. Проинтегрировать ДУ: . 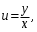 Решение: Сделаем замену или 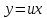 ⇒ ⇒ 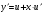 , тогда уравнение примет вид: , тогда уравнение примет вид: 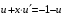 . . Разделяем переменные 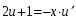 ( (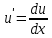 ) )Интегрируем: 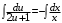 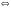 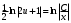 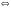 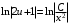 . . После преобразований 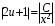 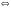 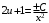 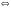 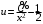 , где , где 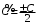 ; и обратной замены получим общий интеграл ; и обратной замены получим общий интеграл 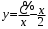 |
