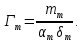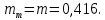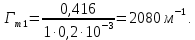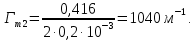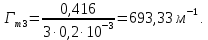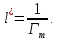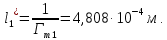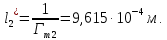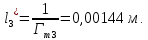Практическая работа
Вариант 18
Задача 1
Определить пористость 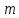 , просветность , просветность 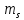 фиктивного грунта, если угол укладки частиц фиктивного грунта, если угол укладки частиц 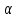 равен равен 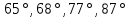 . Построить график зависимости данных величин от угла укладки. . Построить график зависимости данных величин от угла укладки.
Решение
Полная пористость фиктивного грунта определяется по формуле Слихтера:
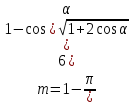
Посчитаем значения полной пористости фиктивного грунта для всех данных углов укладки частиц:
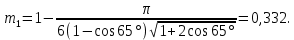
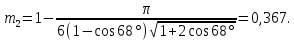
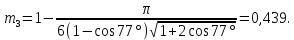
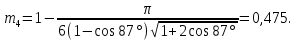
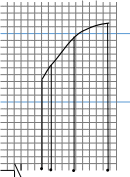
На основании полученных данных построим график зависимости пористости от угла укладки частиц (рис. 1).
Просветность фиктивного грунта вычисляется по формуле
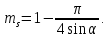
Вычислим для данных значений 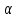 и построим график и построим график 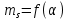 (рис. 2). (рис. 2).
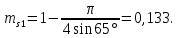
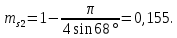
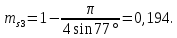
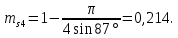


Задача 2
Для величины пористости при 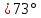 (для 18 варианта) (взять из графика задачи 1) и диаметре частиц (для 18 варианта) (взять из графика задачи 1) и диаметре частиц 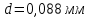 определить удельную поверхность определить удельную поверхность 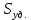 фиктивного грунта, радиус пор идеального грунта фиктивного грунта, радиус пор идеального грунта 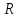 , проницаемость , проницаемость 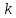 идеального грунта, удельную поверхность, зная проницаемость реального грунта. идеального грунта, удельную поверхность, зная проницаемость реального грунта.
Решение
1. По графику рис. 1 при 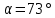 находим, что пористость равна находим, что пористость равна 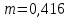 . .
Удельная поверхность фиктивного грунта определяется по формуле
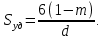
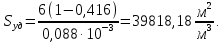
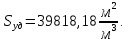
2. Определим радиус пор идеального грунта 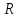 по формуле по формуле
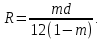
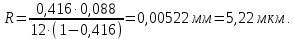
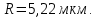
3. Величина проницаемости зависит от размера пор для модели идеального грунта с трубками радиуса 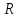 по формуле по формуле
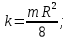
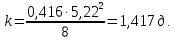
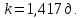
4. По варианту 18 проницаемость реального грунта 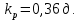
Удельная поверхность реального грунта
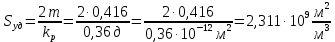
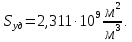
Задача 3
Определить густоту трещин 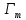 , среднюю длину , среднюю длину 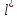 одномерной, двухмерной и трехмерной моделей трещинной среды, если трещинная проницаемость(по варианту 18) одномерной, двухмерной и трехмерной моделей трещинной среды, если трещинная проницаемость(по варианту 18) 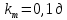 и ширина трещины и ширина трещины 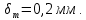
Решение
Для идеализированной трещинной среды трещиноватость 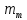 , густота трещин , густота трещин 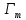 и ширина трещины (или раскрытость) и ширина трещины (или раскрытость) 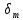 связаны соотношением связаны соотношением
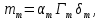
где 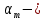 безразмерный коэффициент, равный 1, 2, 3 для одномерного, плоского и пространственного случаев фильтрации, соответственно. безразмерный коэффициент, равный 1, 2, 3 для одномерного, плоского и пространственного случаев фильтрации, соответственно.
Отсюда
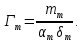
О трещиноватости в задании ничего не сказано, поэтому берем его значение равным 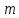 , определенным во второй задаче: , определенным во второй задаче: 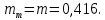
При одномерной фильтрации
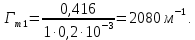
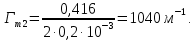
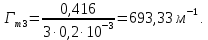
Средняя длина трещинl* равняется среднему размеру блока породы и равна
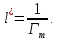
При одномерной фильтрации
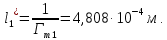
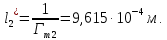
При пространственной фильтрации
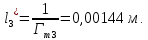 |
 Скачать 141.79 Kb.
Скачать 141.79 Kb. , просветность
, просветность 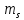 фиктивного грунта, если угол укладки частиц
фиктивного грунта, если угол укладки частиц 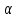 равен
равен 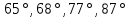 . Построить график зависимости данных величин от угла укладки.
. Построить график зависимости данных величин от угла укладки. 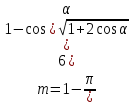
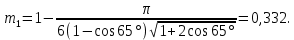
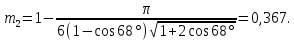
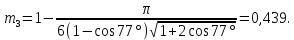
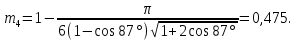
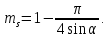
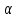 и построим график
и построим график 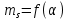 (рис. 2).
(рис. 2).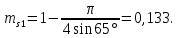


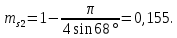
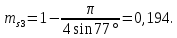
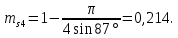



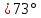 (для 18 варианта) (взять из графика задачи 1) и диаметре частиц
(для 18 варианта) (взять из графика задачи 1) и диаметре частиц 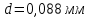 определить удельную поверхность
определить удельную поверхность 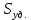 фиктивного грунта, радиус пор идеального грунта
фиктивного грунта, радиус пор идеального грунта 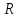 , проницаемость
, проницаемость 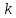 идеального грунта,
идеального грунта, 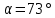 находим, что пористость равна
находим, что пористость равна 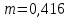 .
.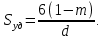
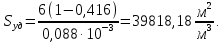
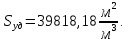
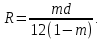
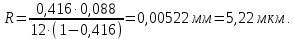
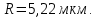
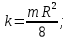
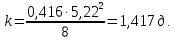
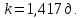
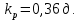
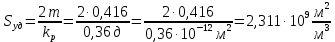
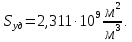
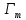 , среднюю длину
, среднюю длину 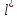 одномерной, двухмерной и трехмерной моделей трещинной среды, если трещинная проницаемость(по варианту 18)
одномерной, двухмерной и трехмерной моделей трещинной среды, если трещинная проницаемость(по варианту 18) 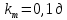 и ширина трещины
и ширина трещины 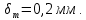
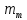 , густота трещин
, густота трещин 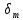 связаны соотношением
связаны соотношением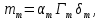
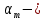 безразмерный коэффициент, равный 1, 2, 3 для одномерного,
безразмерный коэффициент, равный 1, 2, 3 для одномерного,