Работа работа. Решение. Положим a 1 a, b 1 b. Вычислим 1 a 1

• Название: Решение. Положим a 1 a, b 1 b. Вычислим 1 a 1
• Анкор: Работа работа
• Дата: 15.01.2023
• Размер: 46.66 Kb.
• Имя файла: Zadachki.docx
• Тип: Решение; #888067

Задание №2
Магистрант

Корябкин Юрий Сергеевич
Содержание задания

Решить следующие задачи:

1. 
   Найти глобальный максимум целевой функции R=0,5X³+2X²-20X-50 (X<10)
   Найдем максимум функции:
   

f(x) = 0.5•x³+2•x²-20•x-50


Для этого целевую функцию представим в виде: F(max)=-F(min)
-0.5•x³-2•x²+20•x+50
Используем для этого Метод золотого сечения.
Решение.
Положим a₁ = a, b₁ = b. Вычислим λ₁ = a₁ + (1- 0.618)(b₁ - a₁)=3.82, μ₁ = a₁ + 0.618(b₁ - a₁) = 6.18.
Вычислим f(λ₁) = 69.3437, f(μ₁) = -20.7993
Итерация №1.
Поскольку f(λ₁) > f(μ₁), то a₂ = 3.82, b₂ = b₁, λ₂ = 6.18, f(λ₂)=69.3437
μ₂ = a₂ + 0.618(b₂ - a₂) = 3.82 + 0.618(10 - 3.82) = 7.6392, f(7.6392) = -20.7993
Итерация №2.
Поскольку f(λ₂) > f(μ₂), то a₃ = 6.18, b₃ = b₂, λ₃ = 7.6392, f(λ₃)=-20.7993
μ₃ = a₃ + 0.618(b₃ - a₃) = 6.18 + 0.618(10 - 6.18) = 8.5408, f(8.5408) = -136.8365
Итерация №3.
Поскольку f(λ₃) > f(μ₃), то a₄ = 7.6392, b₄ = b₃, λ₄ = 8.5408, f(λ₄)=-136.8365
μ₄ = a₄ + 0.618(b₄ - a₄) = 7.6392 + 0.618(10 - 7.6392) = 9.0982, f(9.0982) = -236.575
Итерация №4.
Поскольку f(λ₄) > f(μ₄), то a₅ = 8.5408, b₅ = b₄, λ₅ = 9.0982, f(λ₅)=-236.575
μ₅ = a₅ + 0.618(b₅ - a₅) = 8.5408 + 0.618(10 - 8.5408) = 9.4426, f(9.4426) = -310.151
Остальные расчеты сведем в таблицу.

N	an	bn	bn-an	λn	μn	F(λn)	F(μn)
1	-	10	10	3.82	6.18	69.3437	-20.7993
2	3.82	10	6.18	6.18	7.6392	-20.7993	-136.8365
3	6.18	10	3.82	7.6392	8.5408	-136.8365	-236.575
4	7.6392	10	2.3608	8.5408	9.0982	-236.575	-310.151
5	8.5408	10	1.4592	9.0982	9.4426	-310.151	-360.4327
6	9.0982	10	0.9018	9.4426	9.6555	-360.4327	-393.4335
7	9.4426	10	0.5574	9.6555	9.7871	-393.4335	-414.5665
8	9.6555	10	0.3445	9.7871	9.8684	-414.5665	-427.922
9	9.7871	10	0.2129	9.8684	9.9187	-427.922	-436.284
10	9.8684	10	0.1316	9.9187	9.9497	-436.284	-441.4971
11	9.9187	10	0.08134	9.9497	9.9689	-441.4971	-444.734
12	9.9497	10	0.05027	9.9689	9.9808	-444.734	-446.7418
13	9.9689	10	0.03107	9.9808	9.9881	-446.7418	-447.9845
14	9.9808	10	0.0192	9.9881	9.9927	-447.9845	-448.7539
15	9.9881	10	0.01187	9.9927	9.9955	-448.7539	-449.2295
16	9.9927	10	0.00734	9.9955	9.9972	-449.2295	-449.5238
17	9.9955	10	0.00453	9.9972	9.9983	-449.5238	-449.7056
18	9.9972	10	0.0028	9.9983	9.9989	-449.7056	-449.818
19	9.9983	10	0.00173	9.9989	9.9993	-449.818	-449.8875
20	9.9989	10	0.00107	9.9993	9.9996	-449.8875	-449.9305
21	9.9993	10	0.000662	9.9996	9.9997	-449.9305	-449.957
22	9.9996	10	0.000409	9.9997	9.9998	-449.957	-449.9734
23	9.9997	10	0.000253	9.9998	9.9999	-449.9734	-449.9836
24	9.9998	10	0.000156	9.9999	9.9999	-449.9836	-449.9899
25	9.9999	10	9.7E-5	9.9999	10	-449.9899	-449.9937
26	9.9999	10	6.0E-5	10	10	-449.9937	-449.9961
27	10	10	3.7E-5	10	10	-449.9961	-449.9976
28	10	10	2.3E-5	10	10	-449.9976	-449.9985
29	10	10	1.4E-5	10	10	-449.9985	-449.9991

|-449.9981-(-449.9988)|≤0.001
Находим x как середину интервала [a,b]:
x=(10+10)/2=9.9999929553879
Ответ: x = 9.9999929553879; F(x) = -449.9988

2. 
   Найти точки экстремума и определить их характер (минимум или максимум, локальный или глобальный минимум и т.п.) следующей функции многих переменных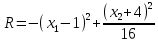
   

z = -(x-1)^2+(y+4)^2/16
1. Найдем частные производные.


2. Решим систему уравнений.
2-2*x = 0

Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 1

Откуда y = -4
Данные значения y подставляем в выражение для x. Получаем: x = 1
Количество критических точек равно 1.
M₁(1;-4)
3. Найдем частные производные второго порядка.



4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).
Вычисляем значения для точки M₁(1;-4)



AC - B² = -1/4 < 0, то глобального экстремума нет.
Вывод: Глобального экстремума нет.

3. 
   Найти оптимальное решение задачи.
   

Фирма, в которой вы трудились, закупает необработанную нефть из нескольких источников W, X, Y, и Z и занимается ее переработкой в различные виды (А, В и С) смазочных масел. Цены для каждого из источников закупки нефти следующие: 17,2; 16,0; 16,7 и 17,5 руб/литр.

Маркетинговая служба фирма определила, что для каждого вида масла рынок в течение года позволяет реализовать 900 тыс., 100 тыс. и 120 тыс. литров по цене 19,0; 18,7 и 18,4 руб/литр соответственно.

Предполагая, что необработанная нефть доступна для покупки из любого источника в неограниченном количестве, сформулируйте и решите задачу максимизации годовой прибыли вашей фирмы, справедливо надеясь, что большая прибыль фирмы может принести вам лично определенное финансовое поощрение.