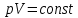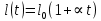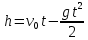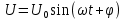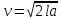Решение практикоориентированных задач с физическим содержанием
 Скачать 134.57 Kb.
|
|
Мастер – класс «Решение практико-ориентированных задач с физическим содержанием» 10 класс Горина Т.Е., учитель математики, высшая квалификационная категория, Самойлова Т.В., учитель физики, высшая квалификационная категория. Тема урока: Решение практико-ориентированных задач с физическим содержанием. Цель урока: разработать рекомендации к системе подготовки решения задач физического содержания. Задачи урока: продолжить формировать умения устанавливать связь между предметами и применять полученные знания по математике при решении различных физических задач; развивать логическое мышление, умение анализировать, делать выводы; развивать познавательный интерес у учащихся через раскрытие практической необходимости и теоретической значимости связи между предметами. Ход урока. Организационный момент. Из информационных источников и анкетирования выпускников школы выявилась одна из проблем: на государственной (итоговой) аттестации в форме ЕГЭ появились задания, отражающие связи с реальной жизнью. Особую сложность вызывают задания № 10 –решение задач с физическим содержанием. Отмечается невысокий процент выполнения задачи №10 (слайд) - Что отличает эту группу заданий? (задачи – объёмные, содержат формулы и часто непонятные величины) - Данные задания не содержатся в учебнике по математике, но мы должны научиться решать их. И сегодня на уроке мы поработаем с кейсом по решению задач с физическим содержанием, подготовленным исследовательской группой, выработаем рекомендации к системе подготовки решения данных задач. ( слайд Тема урока - запись в тетрадь) Актуализация знаний. Задание. Восстановите соответствие: формула – название физического процесса – функциональная зависимость – график функции. Фронтальная работа.
Решение задач. Разбор основных типов задач группы № 10. Известный американский математик Дьёрдь По́йа цитировал: «Хотите научиться решать задачи, то решайте их. Где есть желание, найдётся путь!» Приступим к решению кейса, решим следующие задачи: №1, 6, 9, 14, 19. Есть желающие работать у доски? ( К доске выходят 5 учеников, им предлагаются карточки с заданиями. Первые две задачи подробно разбираются. Остальные решаются самостоятельно). Приступим к решению первой задачи. №1. Высоту над землей подброшенного вертикально вверх мяча вычисляют по формуле  , где h – высота в метрах, t-время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 м?- Внимание! Мяч бросаю вверх (демонстрация опыта). Вопросы: – Каково движение мяча? Как найти высоту подъема мяча? –Объясните физический смысл коэффициентов при t и t2? - Чтобы ответить на вопрос задачи, необходимо найти промежуток времени, когда мяч находился на высоте не менее 10м, т.е., те значения t, при которых h(t) ≥ 10. Решение. Вопрос: Какие знания, умения, навыки,полученные на уроках математики необходимы для решения задачи: - Решение квадратных уравнения или неравенства. - Знание свойств квадратичной функции. (Таблички с ответами на вопросы размещаются на доске) №6. При температуре  рельс имеет длину  м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону  , где  — коэффициент теплового расширения,  — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия. - Внимание на экран. Демонстрация опыта с шариком по тепловому расширению Вопросы: Объясните, почему шарик не проходит через кольцо после его нагревания. – Какие формулы необходимы для расчета конечной длины, объема при линейном, объемном расширении? – Как учитывается данное свойство металлов в технике? - Какая функциональная зависимость выражает линейное расширение? - В этом случае полезно решить задачу так, как вы решаете на уроках физики. - Выразить искомую величину из формулы и подставить значения. Не забыть перевести единицы измерения. Решение. Вопрос: Какие знания, умения, навыки,полученные на уроках математики необходимы для решения задачи: - выражение из данной формулы одной величины через другую. - перевод единиц измерения. №9. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой  , где  — температура нагревателя (в градусах Кельвина),  — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя КПД этого двигателя будет не меньше  , если температура холодильника К? Ответ выразите в градусах Кельвина. Вопрос: Какие знания, умения, навыки, полученные на уроках математики необходимы для решения задачи: - Использование подстановки данных в формулу - решение уравнения с помощью свойства пропорции. Решение. (кратко ученик объясняет, ученики слушают) №14. Уравнение процесса, в котором участвовал газ, записывается в виде  , где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза? Решение. (кратко ученик объясняет, ученики слушают) Вопрос: Какие знания, умения, навыки, полученные на уроках математики необходимы для решения задачи: - Замена переменных. - Тождественные преобразования выражений. - Использование свойств степени. №19. Скорость колеблющегося на пружине груза меняется по закону  (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых. Решение. (кратко ученик объясняет, ученики слушают) Вопрос: Какие знания, умения, навыки, полученные на уроках математики необходимы для решения задачи: - Решение тригонометрического неравенства. - использование свойств тригонометрических функций. Решение кейса. - Что общего в представленных задачах? - Хватит ли вам времени решить все задачи открытого банка задач по математике? (нет, надо уметь решать основные типы задач) Выработаем рекомендации для решения задач блока № 10 (слова появляются на слайде, ученикам раздаются буклеты) Внимательно прочитайте условие, выпишите заданную формулу и данные величины, выявите искомую величину. Проанализируйте условие: необходимо либо выразить искомую величину из формулы и вычислить её, либо подставить данные величины в формулу и решить уравнение или неравенство. Выбрать из полученных решений те, которые удовлетворяют условию задачи. Решение исследовательской задачи по физике. - Задачи по математике с физическим содержанием представляют интерес и для учеников сдающих ЕГЭ по физике в этих задачах повторяют теоретический и практический материал, который необходим для решения задач уровня «А» и «В». - Рассмотрим задачу по физике, решение которой можно провести физическим и математическим методом проще. Задача. Даны два математических маятника, длины нитей которых равны l1 и l2. Определить, во сколько раз период колебания одного маятника больше периода колебаний другого маятника? Предполагаемые ответы: - необходимо подсчитать число колебаний за минуту каждого маятника, найти периоды колебаний и вычислить отношение периодов. - Измерить длину нити, воспользоваться формулой 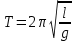 . .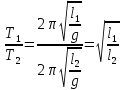Таким образом, для ответа на поставленный вопрос, достаточно измерить длину нити маятника и вычислить отношение периодов по полученной формуле. Вывод: Математический способ решения значительно упрощает ответ на поставленный вопрос физической задачи. Подведение итогов. - Мы сегодня ещё раз нашли точки соприкосновения двух наук – математики и физики. - Математика – это, действительно, царица наук, которая не гнушается выступать и в роли служанки, помогающей нам в покорении вершин других наук. Прав был русский учёный Е. Вагнер, когда говорил, что «Вся глубина мысли, которая заложена в формулировку математических понятий, впоследствии раскрывается тем умением, с которым эти понятия используются» Оценка действий учащихся. - Перед вами на экране представлены графики зависимости уровня ваших знаний от времени, в интервале от начала урока до его завершения. Выберите тот график, который на ваш взгляд наиболее близок вам, принимая во внимание их разный характер. (ответы) - Можно ли по этим графикам судить о скорости приращения ваших знаний в ходе урока? - У кого скорость приращения ваших знаний наивысшая? - Это означает, что мы достигли цели и решили задачи, поставленные в начале урока. Домашнее задание. Задание № 10 содержат не только задачи физического содержания. Найдите в открытом банке задач задачи экономического содержания. Проверьте, подходят ли к их решению рекомендации, выработанные нами на уроке. Приложение Задания № 10 Высоту над землей подброшенного вертикально вверх мяча вычисляют по формуле , где h – высота в метрах, t-время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 м?Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры:  , где  — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь  м , а излучаемая ею мощность P не менее  Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина. Мотоциклист, движущийся по городу со скоростью  км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением  км/ч . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением  . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону  , где  м — начальный уровень воды,  м/мин2, и  м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой  , где  м ,  — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра? 6) При температуре рельс имеет длину м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону , где — коэффициент теплового расширения, — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия. 7) Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:  , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах. 8) В розетку электросети подключены приборы, общее сопротивление которых составляет  Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление  этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями  Ом и Ом их общее сопротивление даeтся формулой  (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах. 9) Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой , где — температура нагревателя (в градусах Кельвина), — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя КПД этого двигателя будет не меньше , если температура холодильника К? Ответ выразите в градусах Кельвина. 10) Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением  , вычисляется по формуле  . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч . 11) Расстояние от наблюдателя, находящегося на небольшой высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле  , где  км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах. 12) При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону  , где  м — длина покоящейся ракеты,  км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с. 13) В ходе распада радиоактивного изотопа его масса уменьшается по закону  , где  (мг) — начальная масса изотопа,  (мин.) — время, прошедшее от начального момента,  (мин.) — период полураспада. В начальный момент времени масса изотопа  мг. Период его полураспада  мин. Через сколько минут масса изотопа будет равна 5 мг? 14) Уравнение процесса, в котором участвовал газ, записывается в виде , где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза? 15) Для обогрева помещения, температура в котором равна  , через радиатор отопления, пропускают горячую воду температурой  . Расход проходящей через трубу воды  кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры  , причeм  (м), где  — теплоeмкость воды,  — коэффициент теплообмена, а  — постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м? 16) Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону  , где — время в секундах, амплитуда  В, частота  /с, фаза  . Датчик настроен так, что если напряжение в нeм не ниже чем  В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть? 17) Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой  , где  м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте  м/с ). При каком наименьшем значении угла (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м? 18) Трактор тащит сани с силой  кН, направленной под острым углом к горизонту. Работа трактора (в килоджоулях) на участке длиной  м вычисляется по формуле  . При каком максимальном угле (в градусах) совершeнная работа будет не менее 2000 кДж? 19) Скорость колеблющегося на пружине груза меняется по закону (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых. 20) По закону Ома для полной цепи сила тока, измеряемая в амперах, равна , где — ЭДС источника (в вольтах), Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более от силы тока короткого замыкания ? (Ответ выразите в омах.) 20) Независимое агентство намерено ввести рейтинг  новостных изданий на основе показателей информативности  , оперативности  и объективности  публикаций. Каждый показатель оценивается целыми числами от -2 до 2.Аналитик, составляющий формулу, считает, что объективность публикаций ценится втрое, а информативность — вдвое дороже, чем оперативность. В результате, формула примет вид  Каким должно быть число  , чтобы издание, у которого все показатели наибольшие, получило рейтинг 30?21) Рейтинг интернет-магазина вычисляется по формуле где  — средняя оценка магазина покупателями (от 0 до 1),  — оценка магазина экспертами (от 0 до 0,7) и  — число покупателей, оценивших магазин.Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 10, их средняя оценка равна 0,9, а оценка экспертов равна 0,35. 22) Некоторая компания продает свою продукцию по цене  руб. за единицу, переменные затраты на производство одной единицы продукции составляют  руб., постоянные расходы предприятия  руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле  . Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб. 23) Зависимость объёма спроса  (единиц в месяц) на продукцию предприятия-монополиста от цены  (тыс. руб.) задаётся формулой  . Выручка предприятия за месяц  (в тыс. руб.) вычисляется по формуле  . Определите наибольшую цену , при которой месячная выручка  составит не менее 240 тыс. руб. Ответ приведите в тыс. руб. |
