статистика 2 практическая работа. Решение Представленный ряд динамики является интервальным рядом динамики с неравными интервалами времени, представленный абсолютными величинами

• Название: Решение Представленный ряд динамики является интервальным рядом динамики с неравными интервалами времени, представленный абсолютными величинами
• Дата: 22.04.2022
• Размер: 87.8 Kb.
• Имя файла: статистика 2 практическая работа.docx
• Тип: Решение; #490823

Задание 2

В таблице  имеются данные об общей численности пенсионеров РФ в исследуемые годы.

год	1995	2000	2005	2007	2008
Численность пенсионеров (тыс. чел.)	37083	38411	38313	38467	38598

Используя данные таблицы 3, выполните задания:

1.     Определите вид статистического ряда, представленного в таблице.

2.     По данным таблицы определите основные показатели динамики.

3.     Определите среднюю численность пенсионеров в исследуемый период. Обоснуйте  применённую Вами формулу.

4.     По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.

Решение

Представленный ряд динамики – является интервальным рядом динамики с неравными интервалами времени, представленный абсолютными величинами.

Рассчитываем цепные и базисные показатели абсолютного прироста, темпов роста и прироста, абсолютного значения 1% прироста, используя методику, приведенную в табл.1.
Таблица 1-Показатели динамики

Показатели	Метод расчета
	цепной (с переменной базой)	базисный (с постоянной базой)
1. Абсолютный прирост ( )
2. Темп роста ( )
3. Темп прироста (Tпр)	;	;
4. Абсолютное значение 1% прироста ( )	;	;

При расчете показателей приняты следующие обозначения: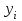

– уровень ряда динамики любого периода, называемый уровнем текущего периода;

– уровень ряда динамики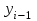 предшествующего периода;

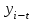– уровень ряда динамики, принятый за постоянную базу сравнения (в нашем примере – начальный, т.е. первый уровень);

Tр(%) – темп роста, выраженный в процентах (умноженный на 100).

Абсолютный прирост:
Цепной:	Базисный:
- 2000г.: тыс.чел.	-2000г.: тыс.чел.
- 2005г.: тыс.чел.	-2005г.: тыс.чел
- 2007г.: тыс.чел.	-2007г.: тыс.чел
- 2008г.: тыс.чел.	-2008г.: тыс.чел
Темп роста:
Цепной:	Базисный:
- 2000г.:	- 2000г.:
- 2005г.:	- 2005г.:
- 2007г.:	- 2007г.:
- 2008г.:	- 2008г.:
Темп прироста:
- 2000г.:	- 2000г.:
- 2005г.:	- 2005г.:
- 2007г.:	- 2007г.:
- 2008г.:	- 2008г.:
Абсолютное значение 1% прироста:
-2000г.: тыс.чел.
-2005г.: тыс.чел.
-2007г.: тыс.чел.
-2008г.: тыс.чел.

Рассчитываем среднюю численность пенсионеров по формуле средней арифметической взвешенной так как ряд интервальный с неравными промежутками времени: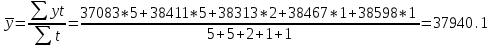

_{тыс.чел.}

Представим графически динамику пенсионеров.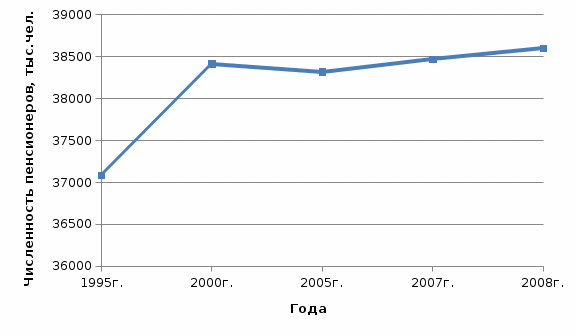



Рис.1- Динамика численности пенсионеров за 1995-2008гг.
Выводы: в 2000г. по сравнению с 1995г. численность пенсионеров выросла на 1328 тыс.чел., что составляет 3,6%. В 2005г. по сравнению с 2000г. численность пенсионеров сократилась на 98 тыс.чел., что составляет 0,3% а по сравнению с 1995г. численность выросла на 1230 тыс.чел. что составляет 3,3%.

В 2007г. по сравнению с 2005г. численность пенсионеров выросла на 154 тыс.чел., что составляет 0,4% а по сравнению с 1995г. численность выросла на 1384 тыс.чел. что составляет 3,7%.

В 2008г. по сравнению с 2007г. численность пенсионеров выросла на 131 тыс.чел., что составляет 0,3% а по сравнению с 1995г. численность выросла на 1515 тыс.чел. что составляет 4,1%.

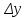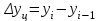
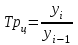
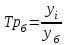
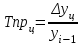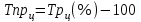
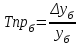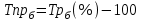
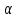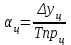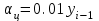
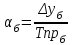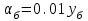
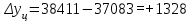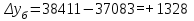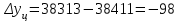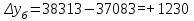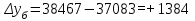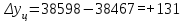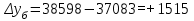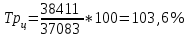
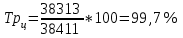
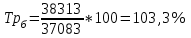
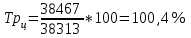
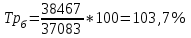
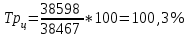
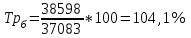
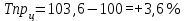
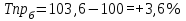
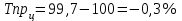
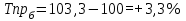
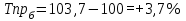
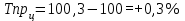
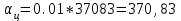Среднегодовая численность пенсионеров за 1995-2008гг. составила 37940,1 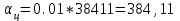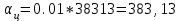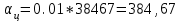тыс.чел.