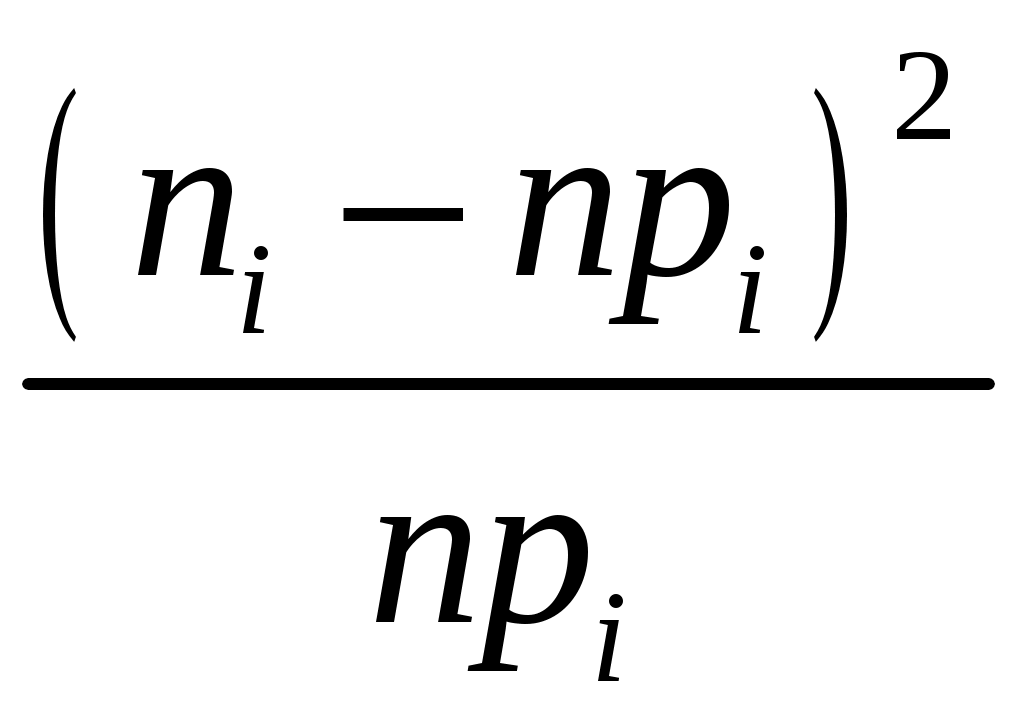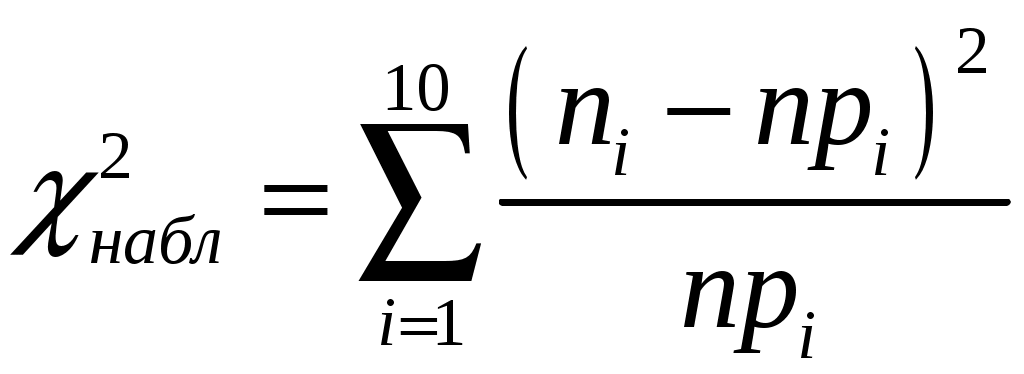По данным выборки установить теоретический закон распределения случайной величины и проверить согласованность статистического и теоретического распределений по критерию Пирсона при уровне значимости 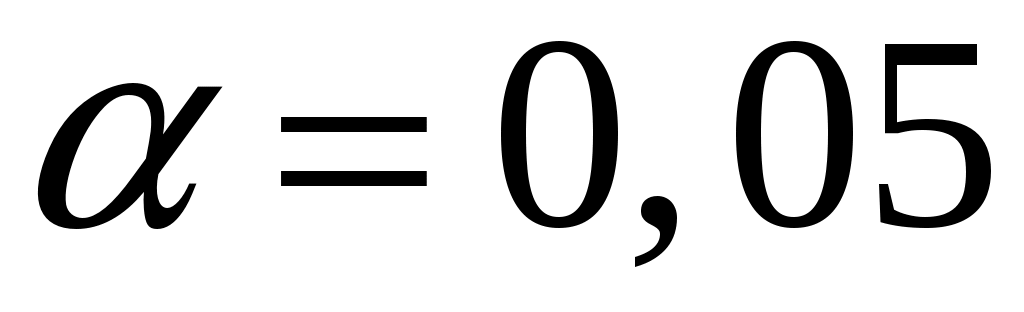 . .
Решение.
1. Предварительная обработка выборочных данных.
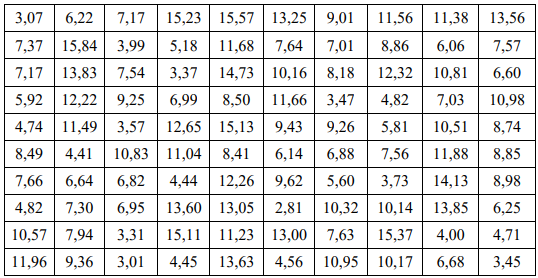
Составим вариационный ряд – упорядоченную последовательность данных выборки.
2,81
|
4,00
|
5,60
|
6,82
|
7,54
|
8,50
|
9,62
|
10,98
|
12,22
|
13,83
|
3,01
|
4,41
|
5,81
|
6,88
|
7,56
|
8,74
|
10,14
|
11,04
|
12,26
|
13,85
|
3,07
|
4,44
|
5,92
|
6,95
|
7,57
|
8,85
|
10,16
|
11,23
|
12,32
|
14,13
|
3,31
|
4,45
|
6,06
|
6,99
|
7,63
|
8,86
|
10,17
|
11,38
|
12,65
|
14,73
|
3,37
|
4,56
|
6,14
|
7,01
|
7,64
|
8,98
|
10,32
|
11,49
|
13,00
|
15,11
|
3,45
|
4,71
|
6,22
|
7,03
|
7,66
|
9,01
|
10,51
|
11,56
|
13,05
|
15,13
|
3,47
|
4,74
|
6,25
|
7,17
|
7,94
|
9,25
|
10,57
|
11,66
|
13,25
|
15,23
|
3,57
|
4,82
|
6,60
|
7,17
|
8,18
|
9,26
|
10,81
|
11,68
|
13,56
|
15,37
|
3,73
|
4,82
|
6,64
|
7,30
|
8,41
|
6,36
|
10,83
|
11,88
|
13,60
|
15,57
|
3,99
|
5,18
|
6,68
|
7,37
|
8,49
|
9,43
|
10,95
|
11,96
|
13,63
|
15,84
|
Наименьшее значение совокупности 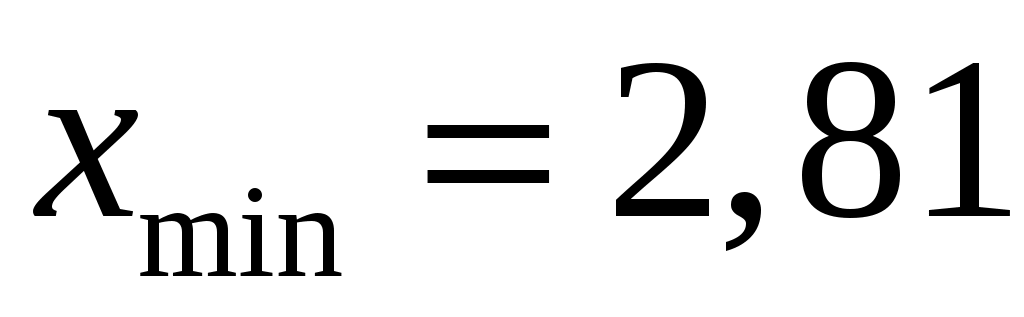 ; наибольшее ; наибольшее 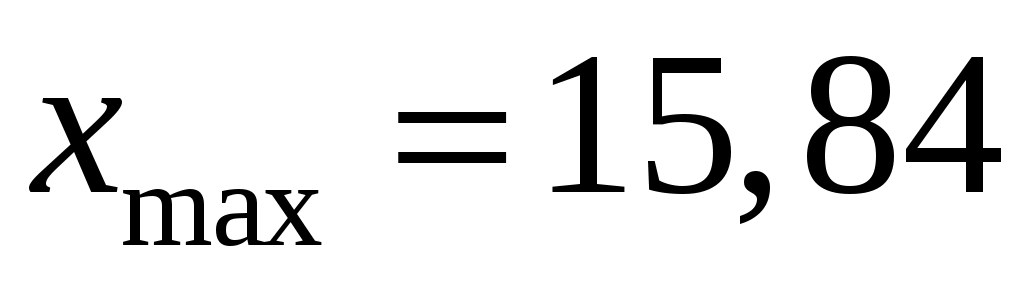 , объем выборки , объем выборки 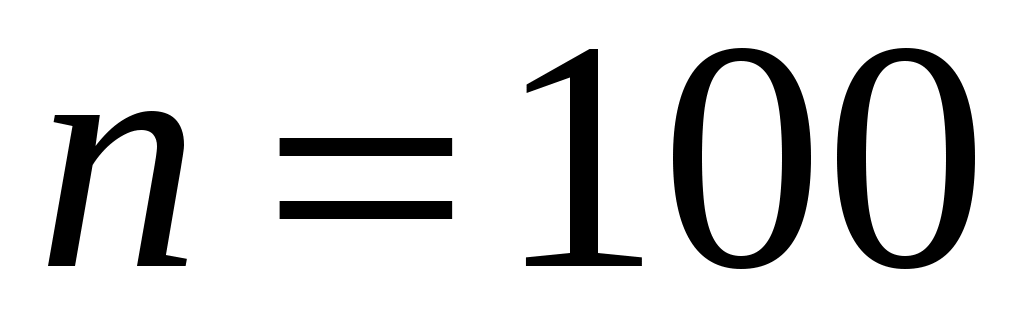 . Для дальнейшей обработки выборки разобьем вариационный ряд на частотные интервалы – разряды. Для выборки такого объема рекомендуется выбирать число интервалов от 7 до 15. Округлим, граничные величины так, чтобы все данные выборки вошли в границы. При этом длины интервалов . Для дальнейшей обработки выборки разобьем вариационный ряд на частотные интервалы – разряды. Для выборки такого объема рекомендуется выбирать число интервалов от 7 до 15. Округлим, граничные величины так, чтобы все данные выборки вошли в границы. При этом длины интервалов 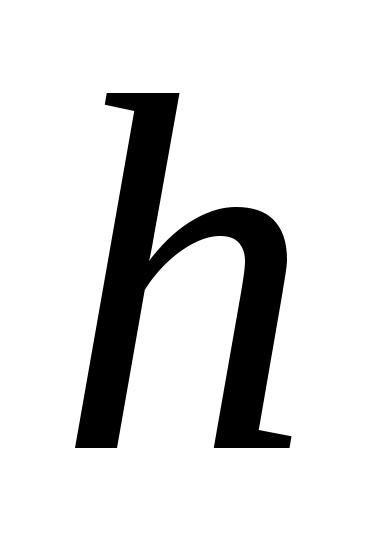 выбираем равными так, чтобы их величина была удобной для обработки. Будем исследовать диапазон статистических данных на интервале выбираем равными так, чтобы их величина была удобной для обработки. Будем исследовать диапазон статистических данных на интервале 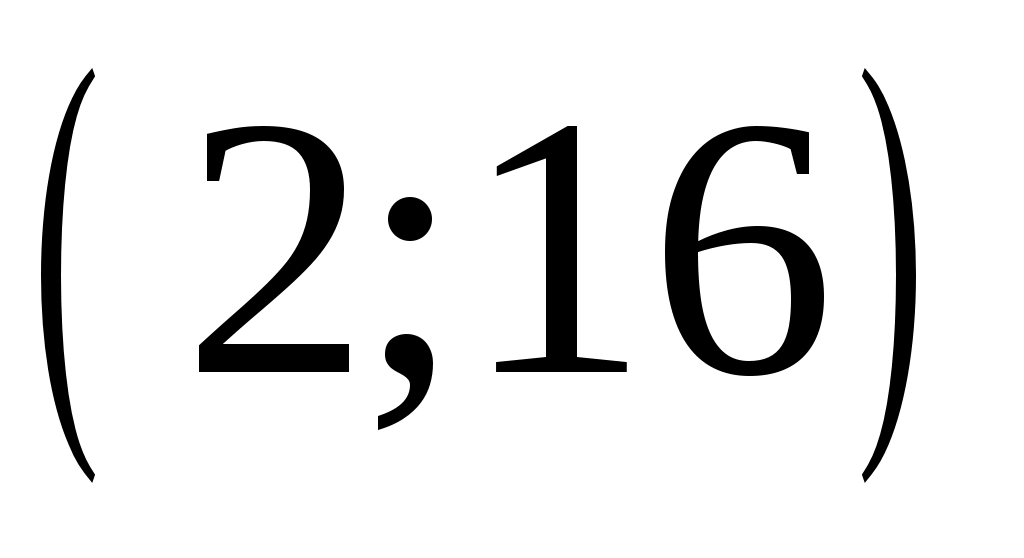 , выберем число частотных интервалов , выберем число частотных интервалов 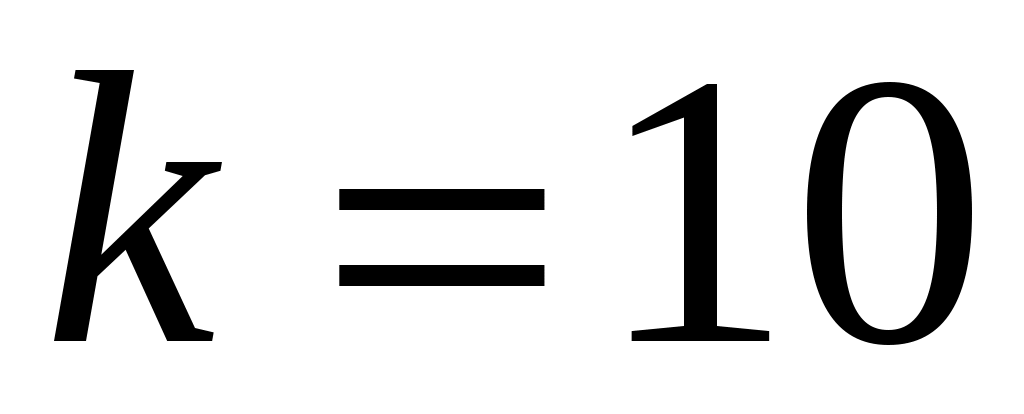 , тогда длина каждого частотного интервала (разряда) равна: , тогда длина каждого частотного интервала (разряда) равна:
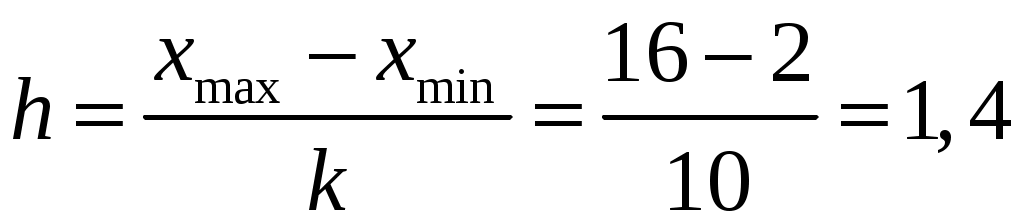 . .
Предварительно покажем распределение выборочных данных по частотным интервалам в виде диаграммы точек, каждая из которых соответствует одному данному выборки.
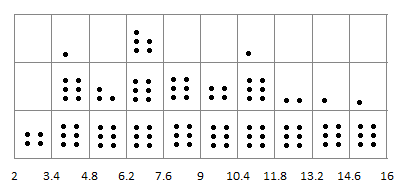
Построим дискретный статистический ряд и гистограмму распределения (гистограмму относительных частот), для этого составим таблицу содержащую следующие данные:
1. Частотные интервалы (разряды) с указанием границ.
2. Число данных выборки (точек измерения) на интервале – 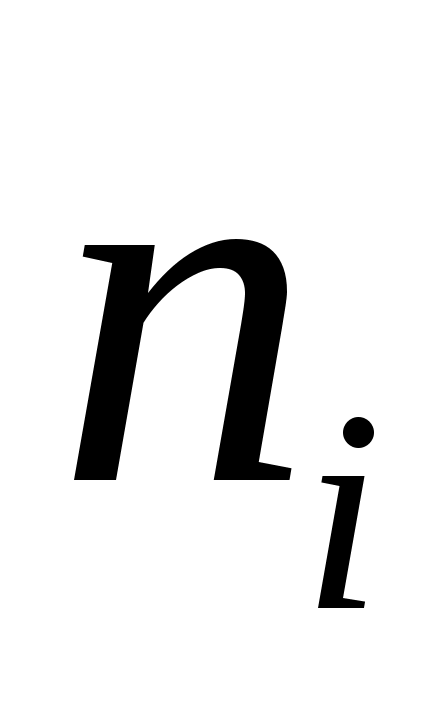 . .
3. Относительная частота данных выборки 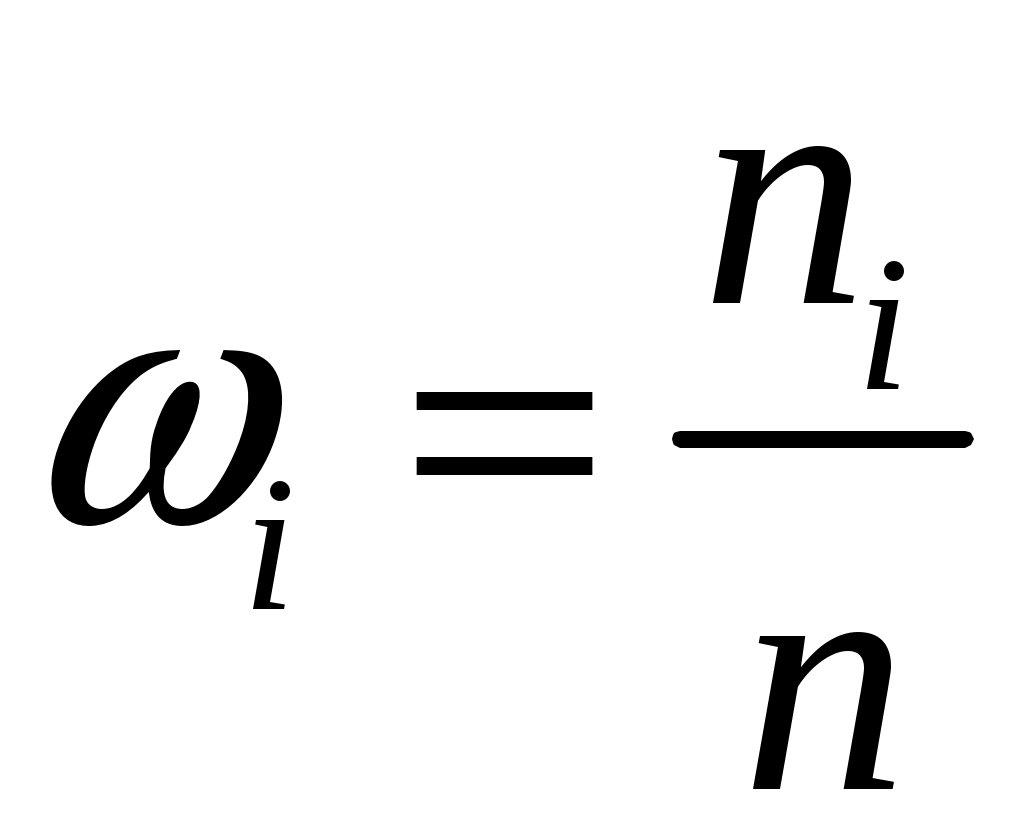 . .
4. Плотность относительной частоты данных 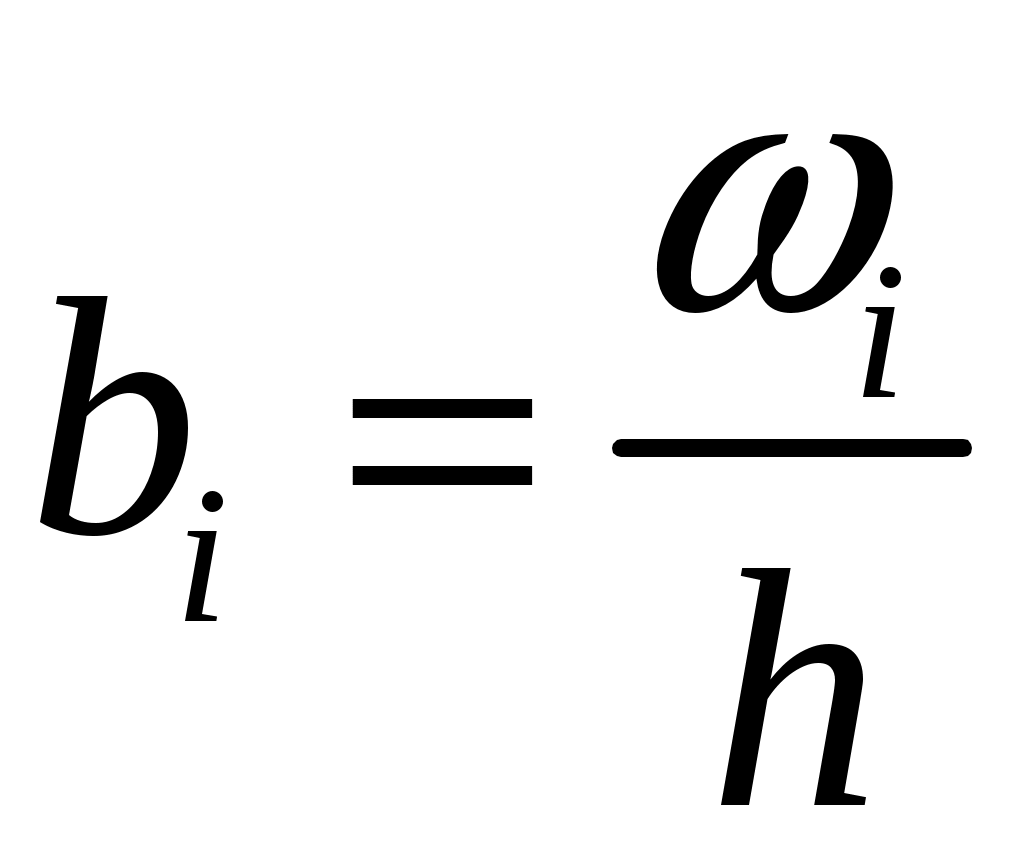 . .
5. Середины частотных интервалов – 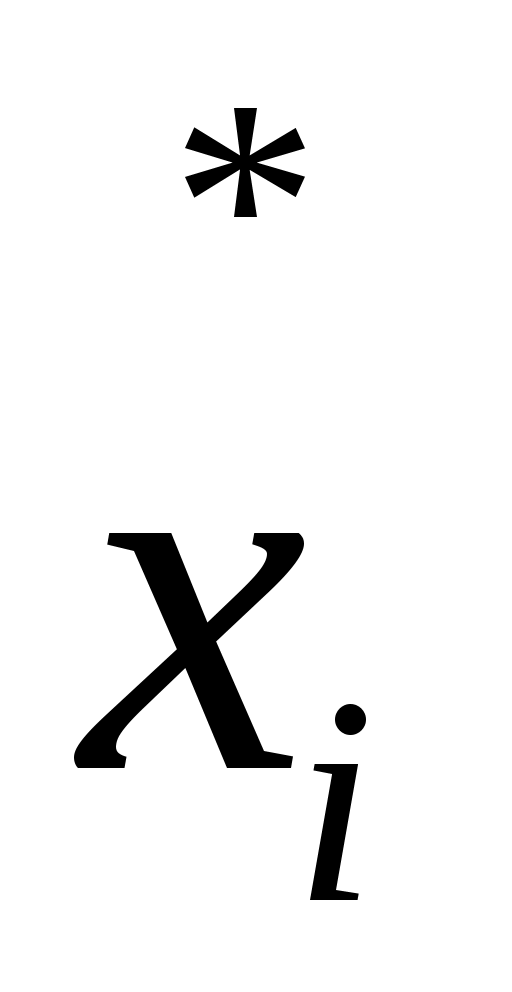 . .
Разряды
|
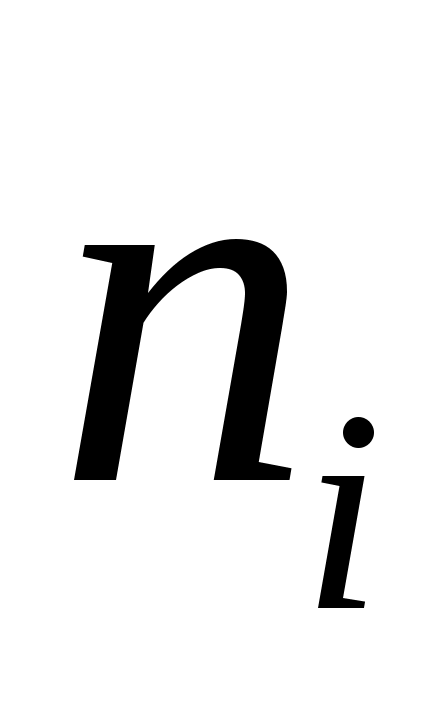
|

|
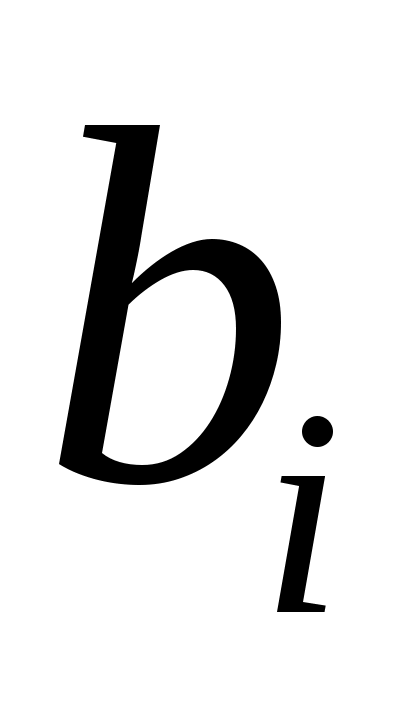
|
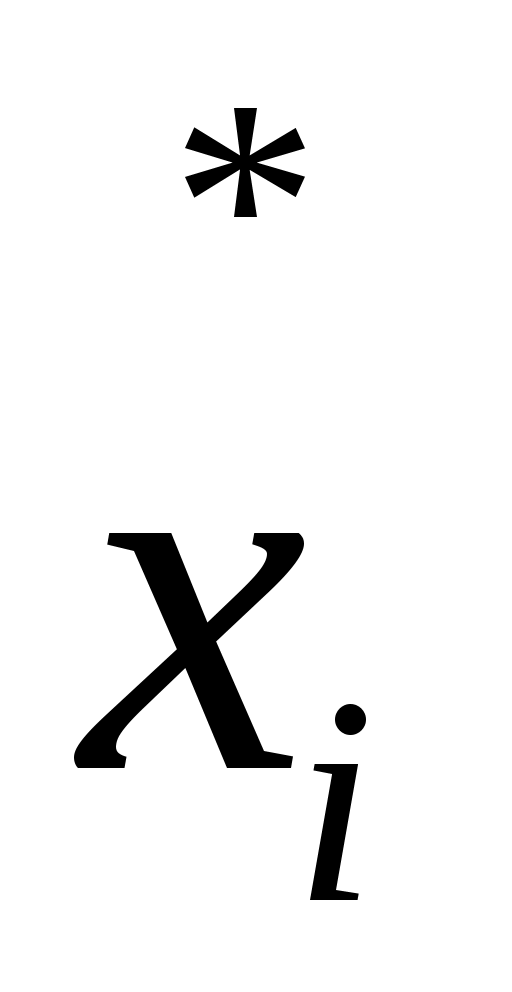
|
2 – 3,4
|
4
|
0.04
|
0.02
|
2.7
|
3,4 – 4,8
|
13
|
0.13
|
0.065
|
4.1
|
4,8 – 6,2
|
9
|
0.09
|
0.045
|
5.5
|
6,2 – 7,6
|
17
|
0.17
|
0.085
|
6.9
|
7,6 – 9,0
|
12
|
0.12
|
0.06
|
8.3
|
9,0 – 10,4
|
10
|
0.1
|
0.05
|
9.7
|
10,4 – 11,8
|
13
|
0.13
|
0.065
|
11.1
|
11,8 – 13,2
|
8
|
0.08
|
0.04
|
12.5
|
13,2 – 14,6
|
7
|
0.07
|
0.035
|
13.9
|
14,6 – 16,0
|
7
|
0.07
|
0.035
|
15.3
|
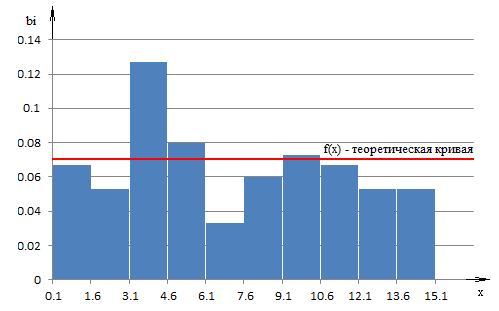
Построим гистограмму распределения.
2. Определение параметров статистического распределения (выборочных характеристик).
Составим таблицу.
Для вычисления несмещенных точечных оценок параметров распределения составим таблицу.
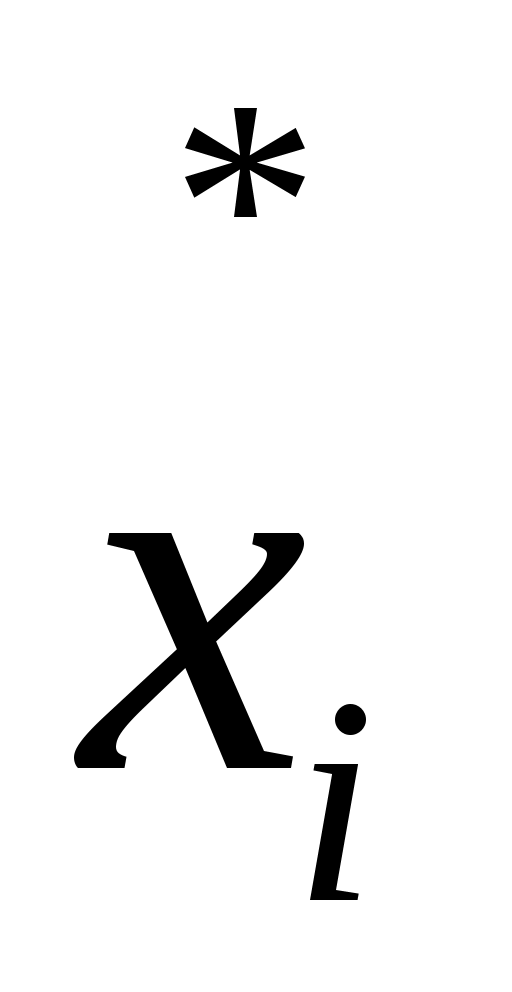
|
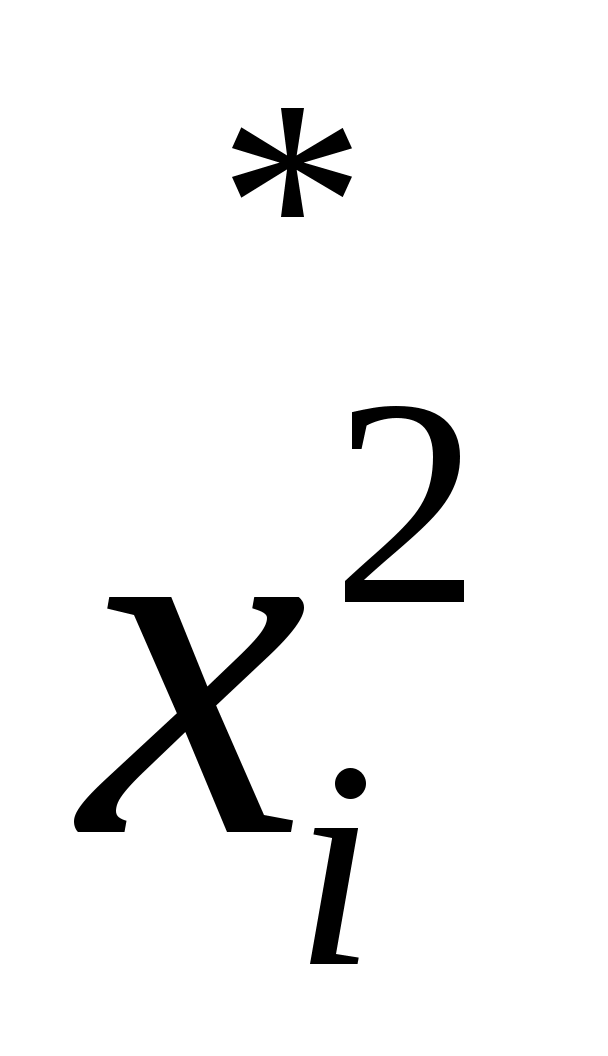
|

|
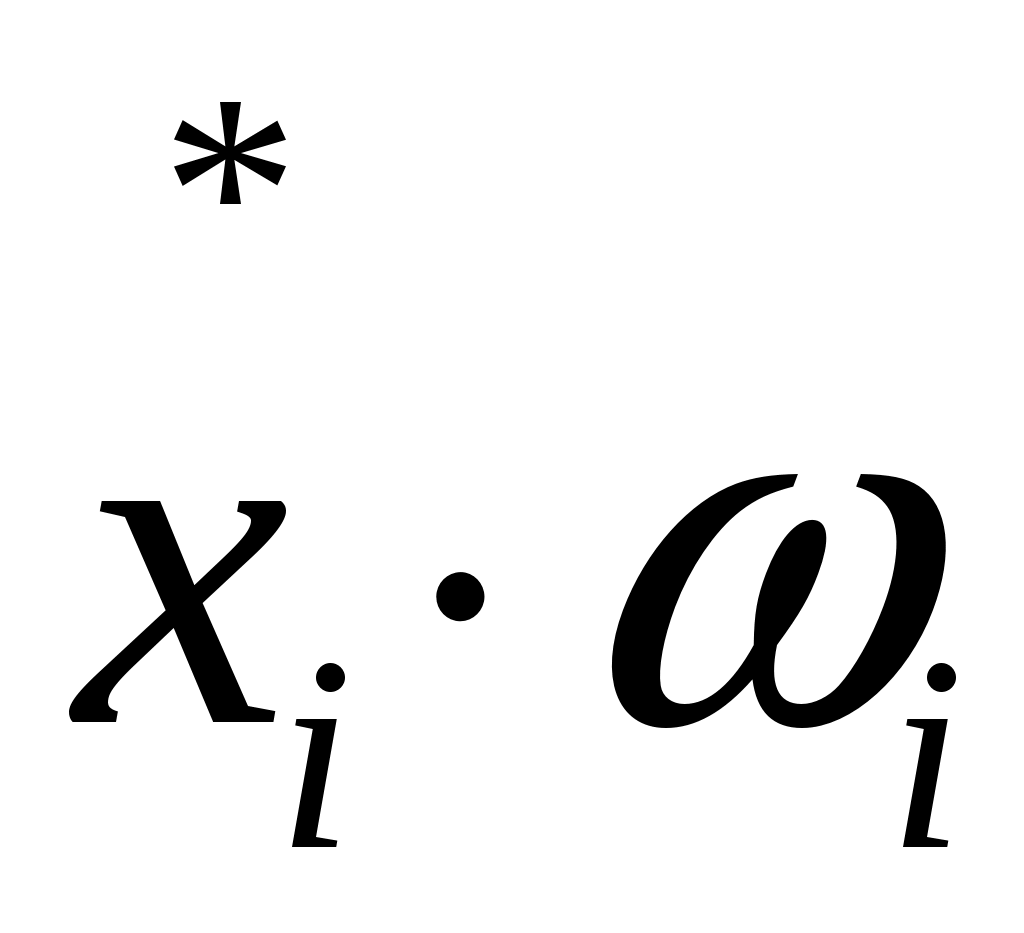
|
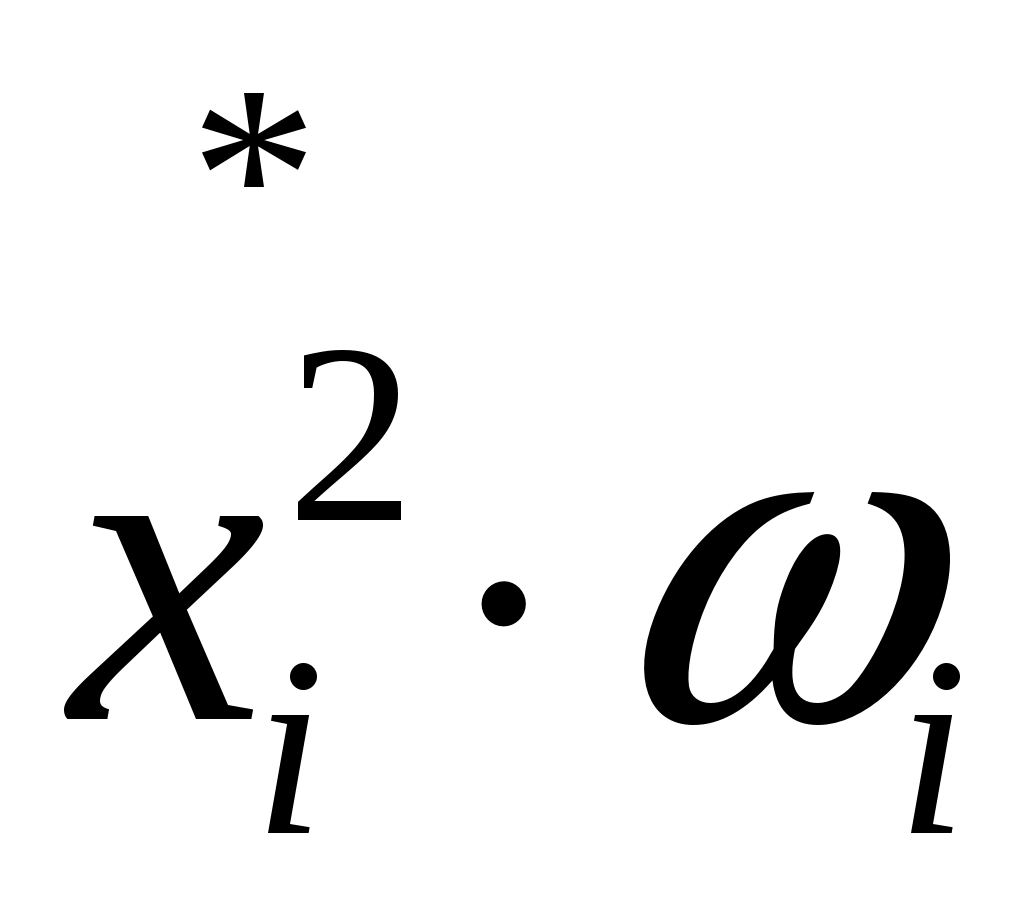
|
2.7
|
7.29
|
0.04
|
0.108
|
0.2916
|
4.1
|
16.81
|
0.13
|
0.533
|
2.1853
|
5.5
|
30.25
|
0.09
|
0.495
|
2.7225
|
6.9
|
47.61
|
0.17
|
1.173
|
8.0937
|
8.3
|
68.89
|
0.12
|
0.996
|
8.2668
|
9.7
|
94.09
|
0.1
|
0.97
|
9.409
|
11.1
|
123.21
|
0.13
|
1.443
|
16.0173
|
12.5
|
156.25
|
0.08
|
1
|
12.5
|
13.9
|
193.21
|
0.07
|
0.973
|
13.5247
|
15.3
|
234.09
|
0.07
|
1.071
|
16.3863
|
|
|
|
8.762
|
89.3972
|
Начальные эмпирические моменты первого и второго порядка:

Центральный эмпирический момент второго порядка:
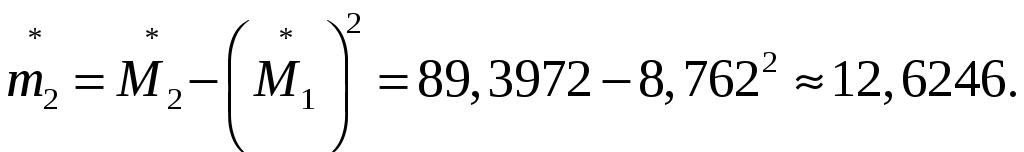
Параметры статистического распределения.
Выборочная средняя 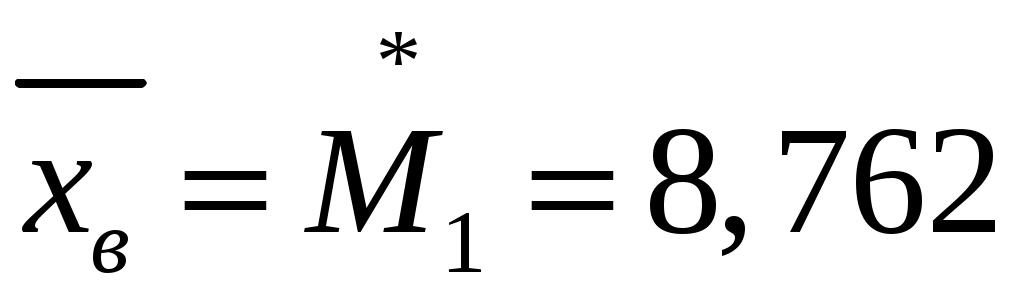 ‒ статистическая оценка математического ожидания случайной величины по данным выборки; ‒ статистическая оценка математического ожидания случайной величины по данным выборки;
Выборочная дисперсия 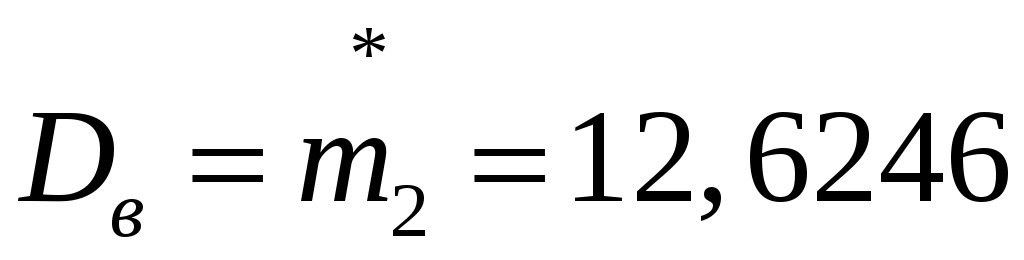 – статистическая оценка дисперсии случайной величины по данным выборки; – статистическая оценка дисперсии случайной величины по данным выборки;
Выборочное среднеквадратическое отклонение
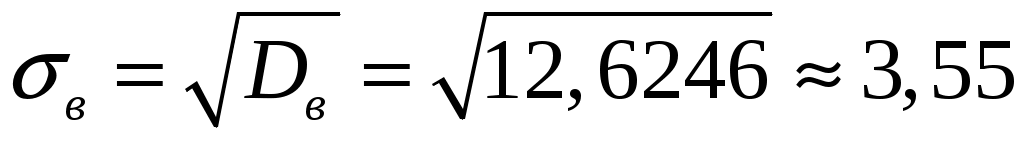 . .
3. Выбор и проверка гипотезы о виде теоретического закона распределения генеральной совокупности
По виду гистограммы выдвигаем нулевую гипотезу 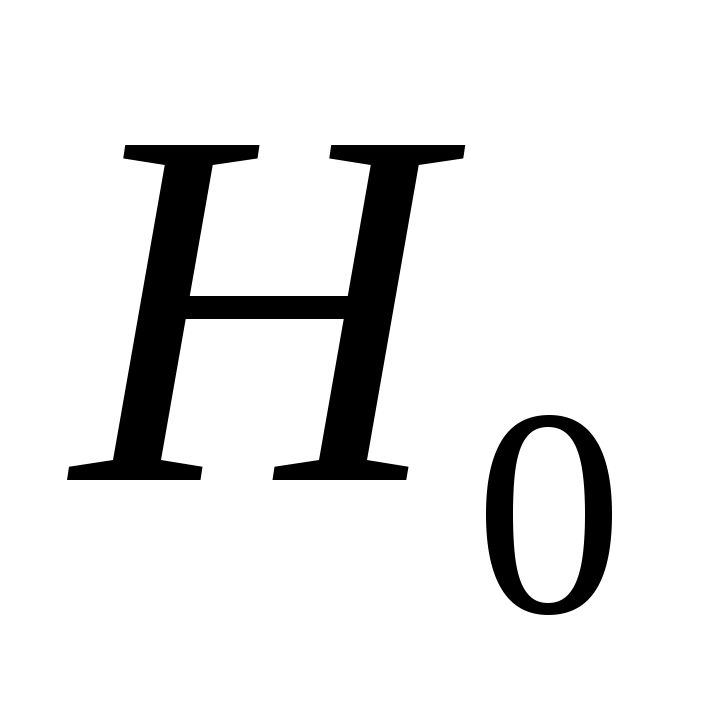 о равномерном законе распределения исследуемого статистического материала. Плотность равномерного распределения определяется функцией о равномерном законе распределения исследуемого статистического материала. Плотность равномерного распределения определяется функцией
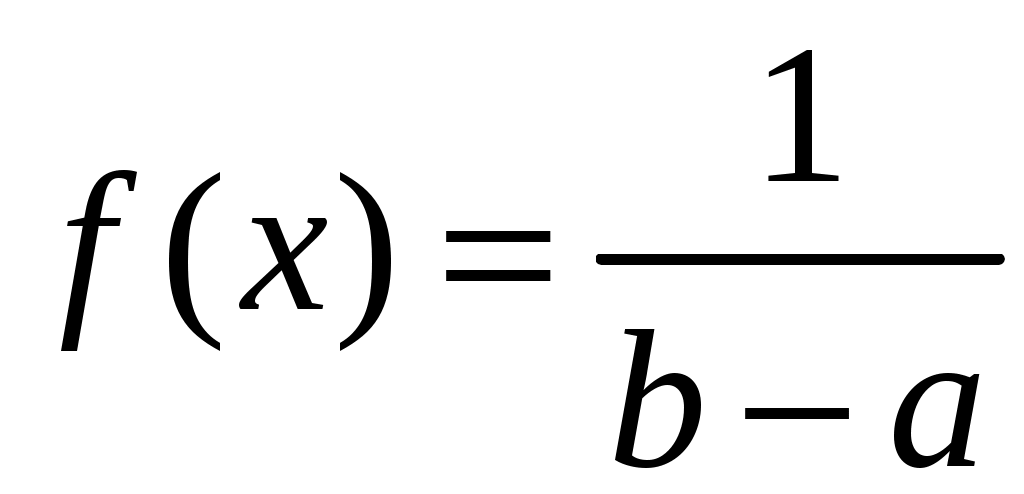 , ,
где, используя метод моментов, параметры 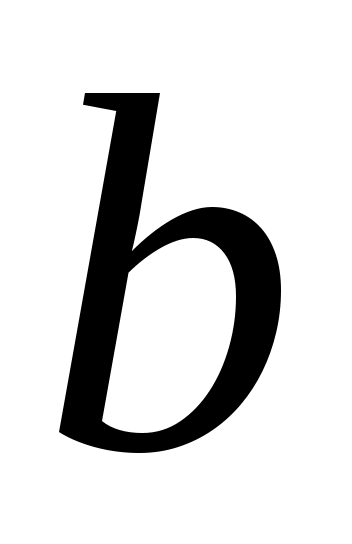 и и  определяем, как оценки математического ожидания и среднеквадратического отклонения по представленной выборке: определяем, как оценки математического ожидания и среднеквадратического отклонения по представленной выборке:
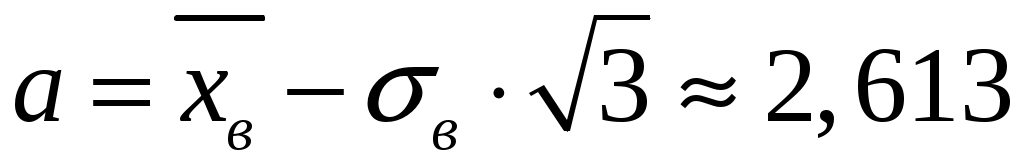 ; ; 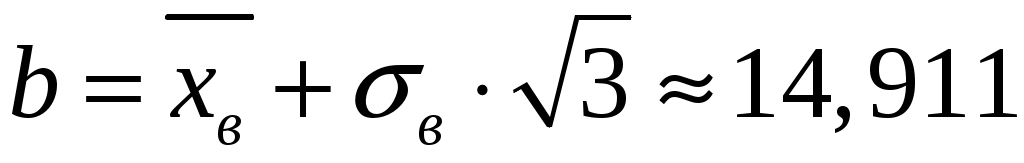 . .
Тогда теоретическая кривая распределения описывается функцией, график которой построим на гистограмме
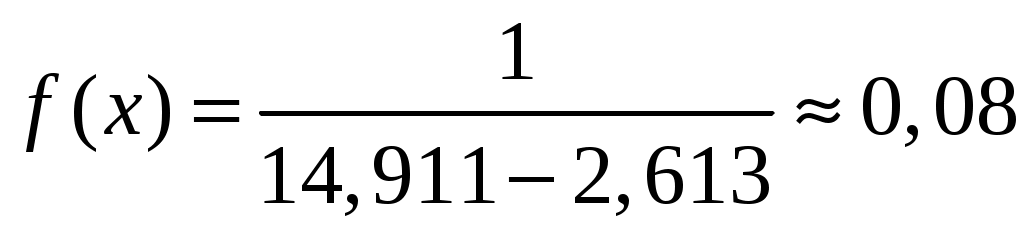 . .
Проверим нулевую гипотезу 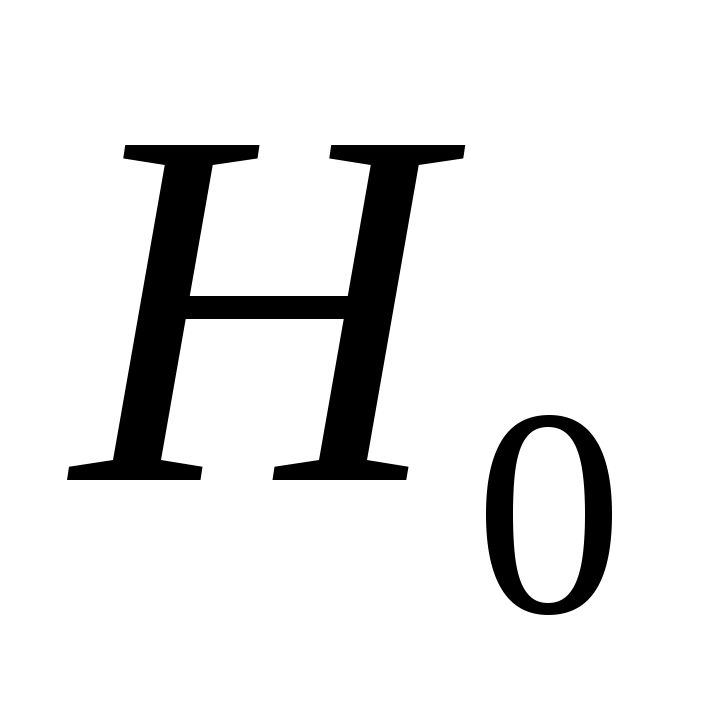 о нормальном распределении статистических данных с параметрами о нормальном распределении статистических данных с параметрами 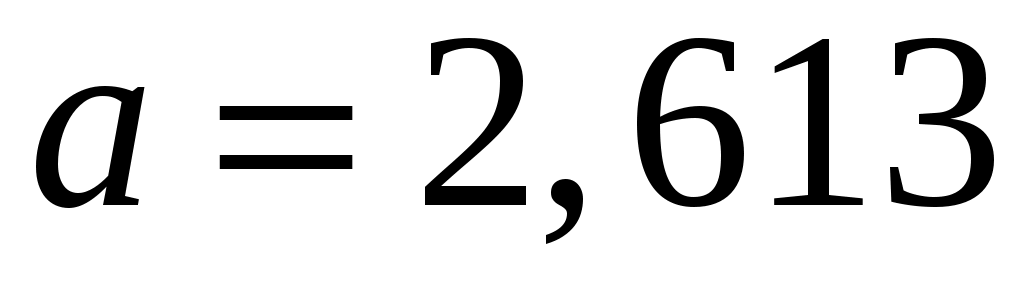 и и 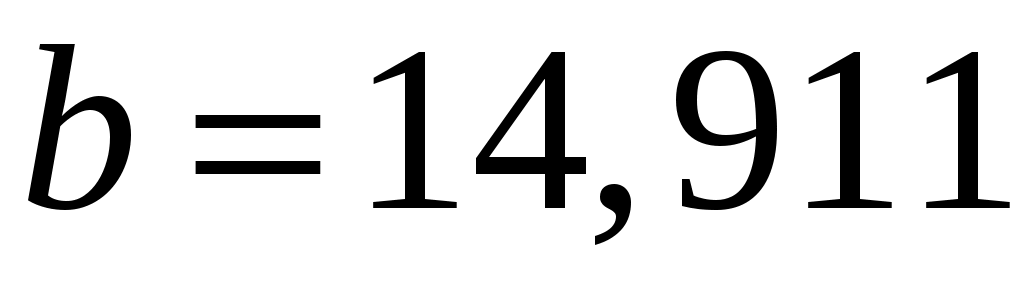 по критерию Пирсона. Найдем наблюдаемое значение по критерию Пирсона. Найдем наблюдаемое значение 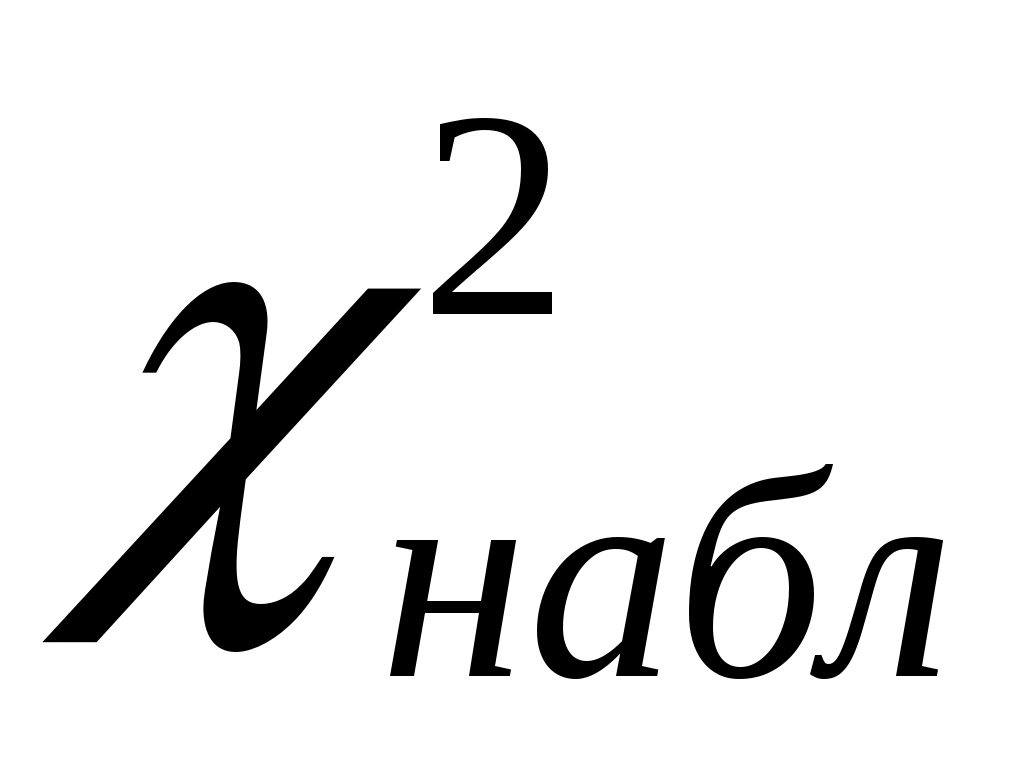 . Для промежуточных вычислений и построения графика сглаживающей теоретической функции составим расчетную таблицу. . Для промежуточных вычислений и построения графика сглаживающей теоретической функции составим расчетную таблицу.
|
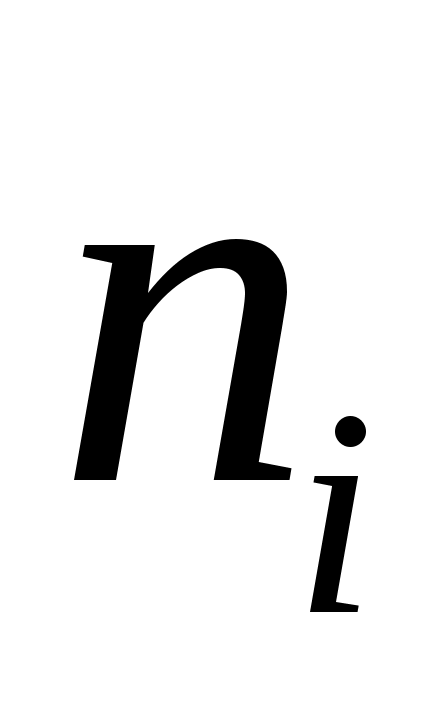
|
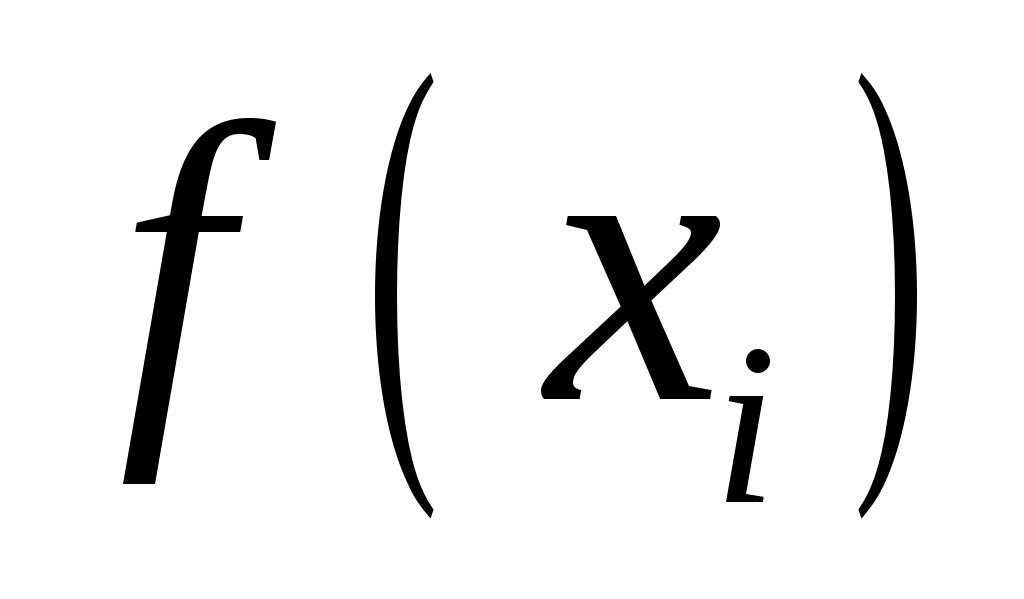
|
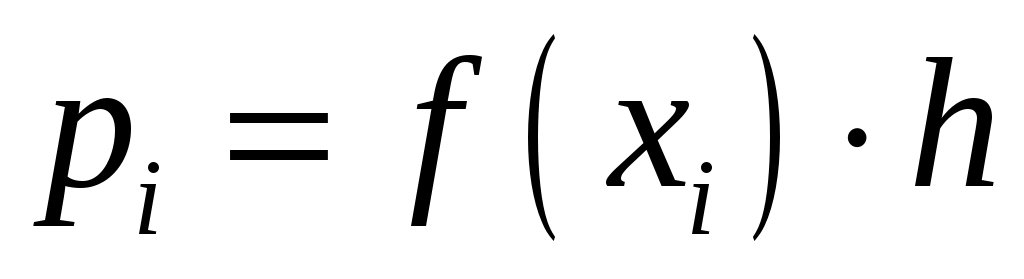
|
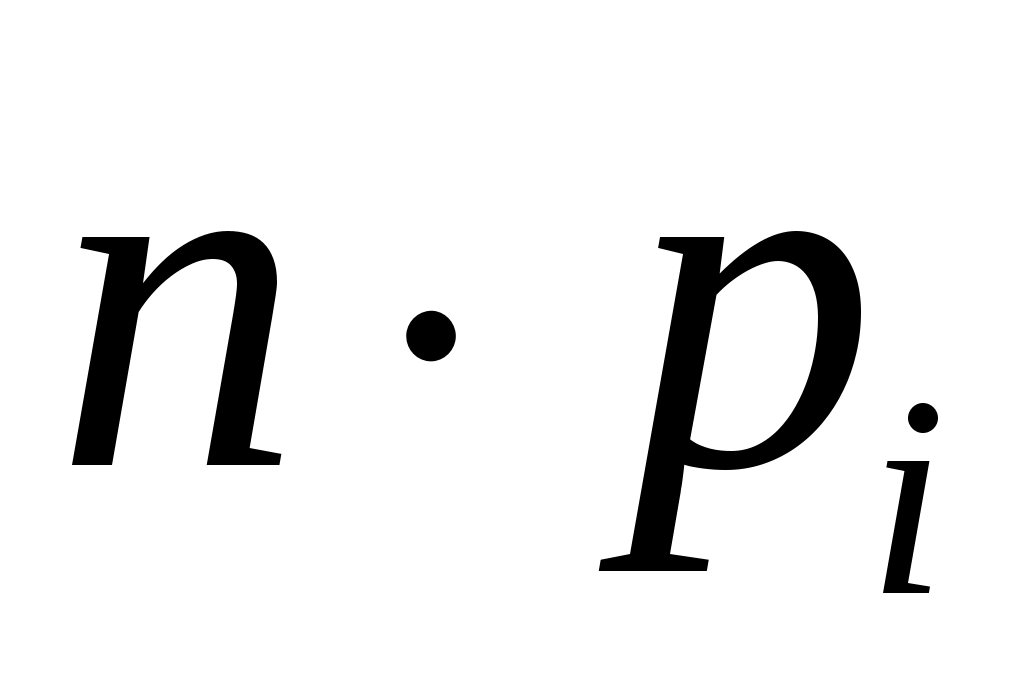
|
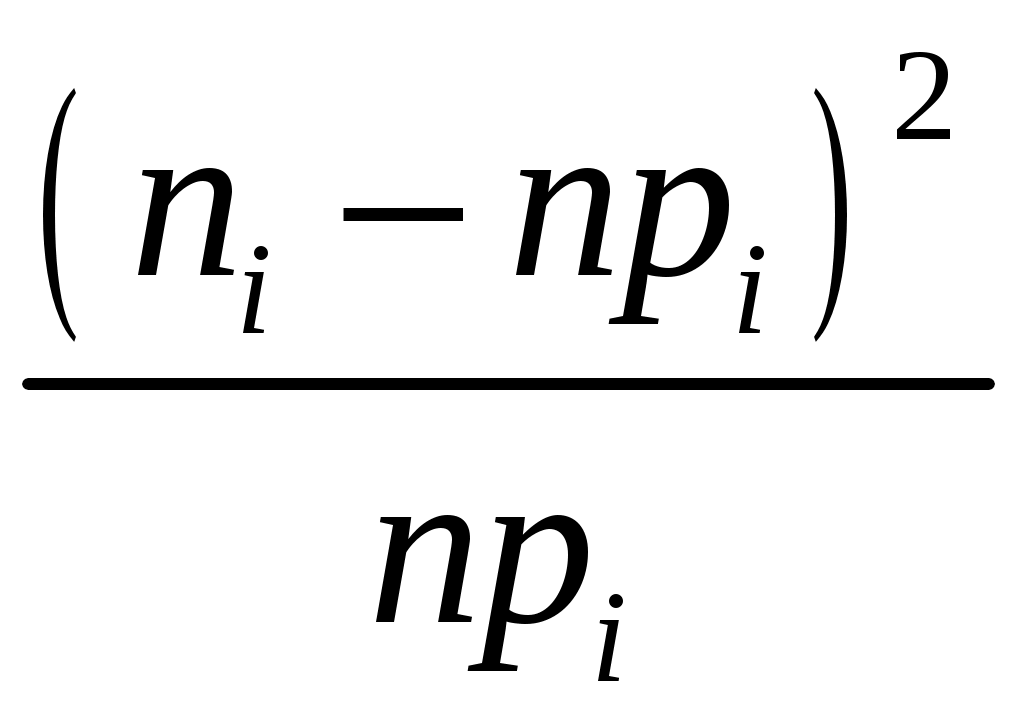
|
2.7
|
4
|
0.08
|
0.112
|
11.2
|
4.629
|
4.1
|
13
|
0.08
|
0.112
|
11.2
|
0.289
|
5.5
|
9
|
0.08
|
0.112
|
11.2
|
0.432
|
6.9
|
17
|
0.08
|
0.112
|
11.2
|
3.004
|
8.3
|
12
|
0.08
|
0.112
|
11.2
|
0.057
|
9.7
|
10
|
0.08
|
0.112
|
11.2
|
0.129
|
11.1
|
13
|
0.08
|
0.112
|
11.2
|
0.289
|
12.5
|
8
|
0.08
|
0.112
|
11.2
|
0.914
|
13.9
|
7
|
0.08
|
0.112
|
11.2
|
1.575
|
15.3
|
7
|
0.08
|
0.112
|
11.2
|
1.575
|
Сумма 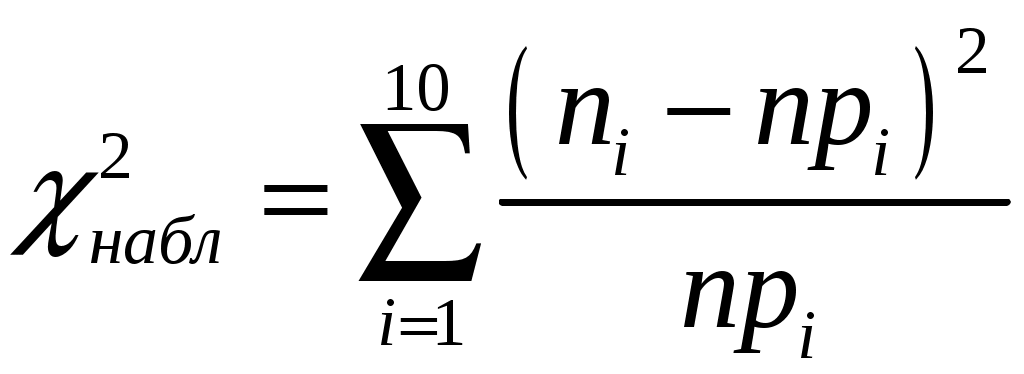
|
12,893
|
Число степеней свободы для распределения, которое описывается двумя параметрами равно 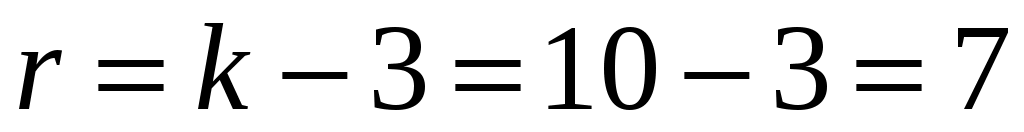 . Воспользуемся таблицей критических значений распределения . Воспользуемся таблицей критических значений распределения 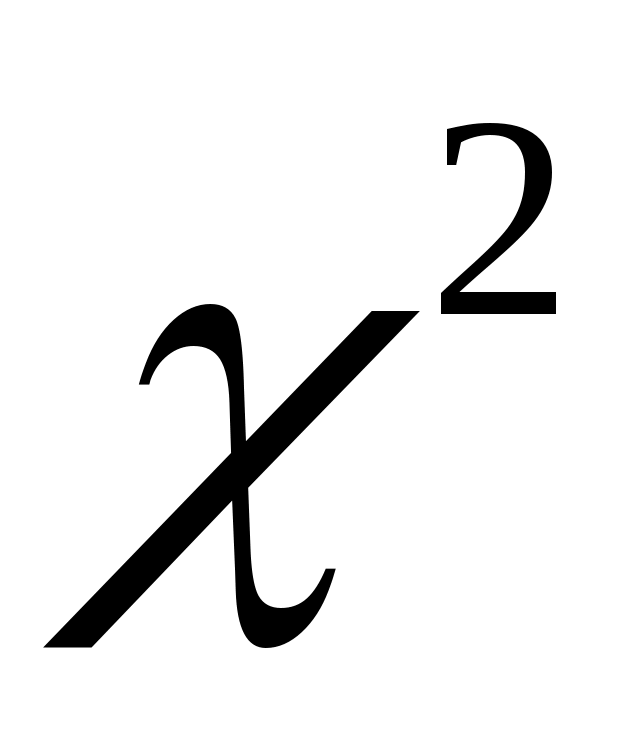 . Согласно заданному уровню значимости . Согласно заданному уровню значимости 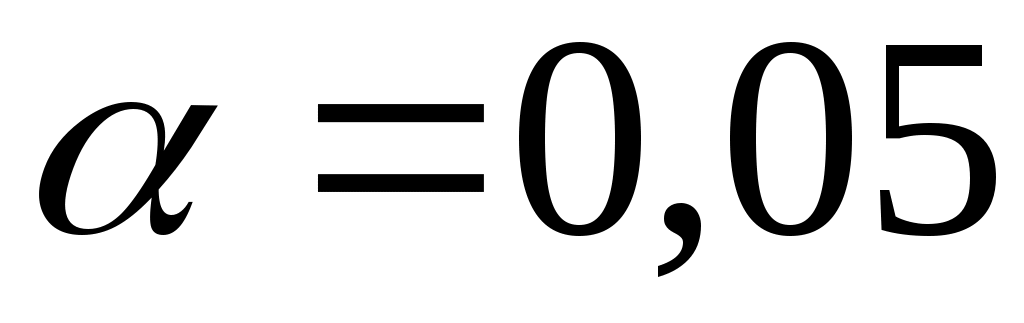 и установленному числу степеней свободы найдем критическое значение и установленному числу степеней свободы найдем критическое значение 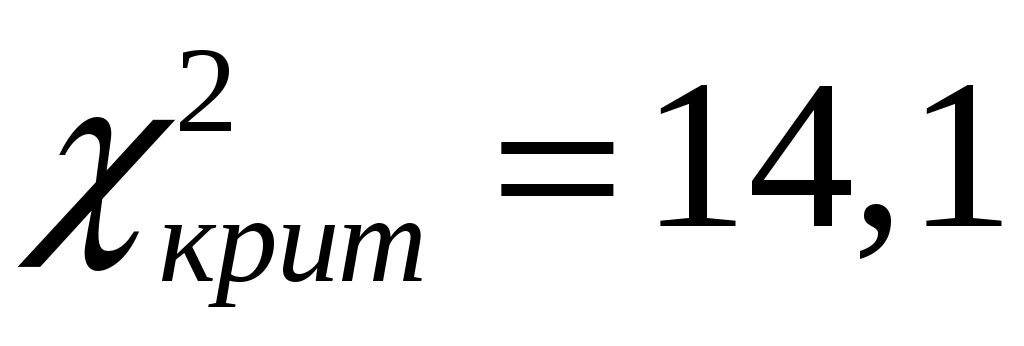 . Так как . Так как 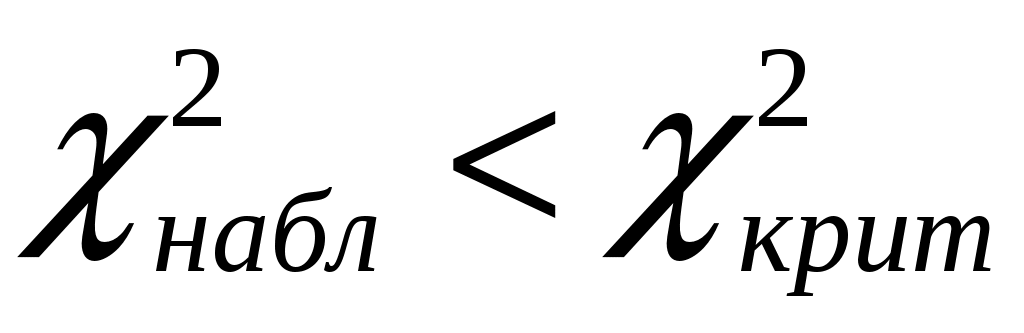 , то нулевая гипотеза принимается. Следовательно, по данной выборке можно принять равномерный закон распределения генеральной совокупности статистических данных. , то нулевая гипотеза принимается. Следовательно, по данной выборке можно принять равномерный закон распределения генеральной совокупности статистических данных.
|
 Скачать 380.5 Kb.
Скачать 380.5 Kb.
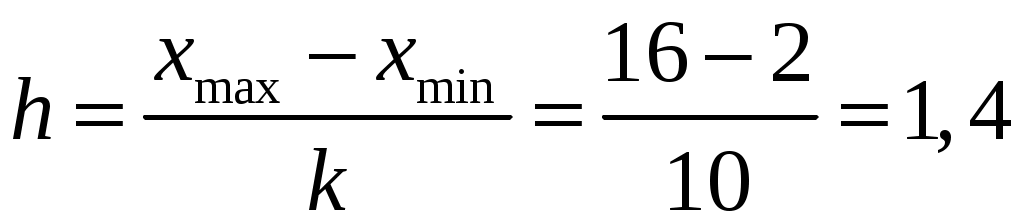 .
.
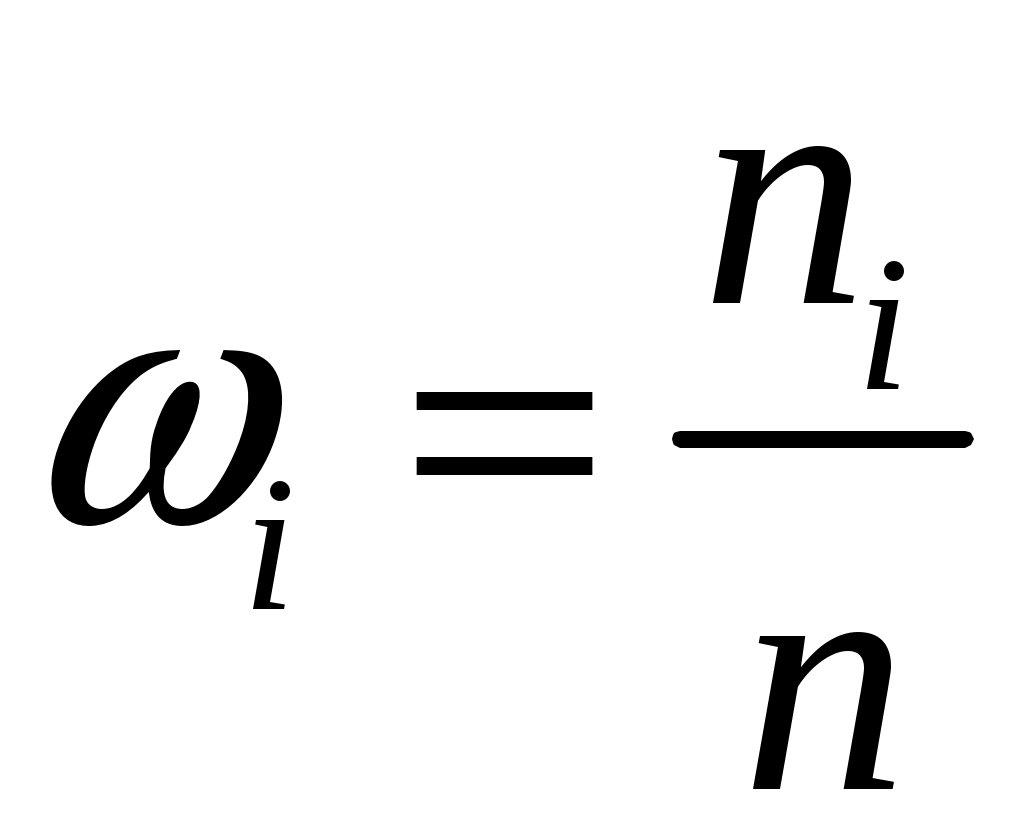 .
. 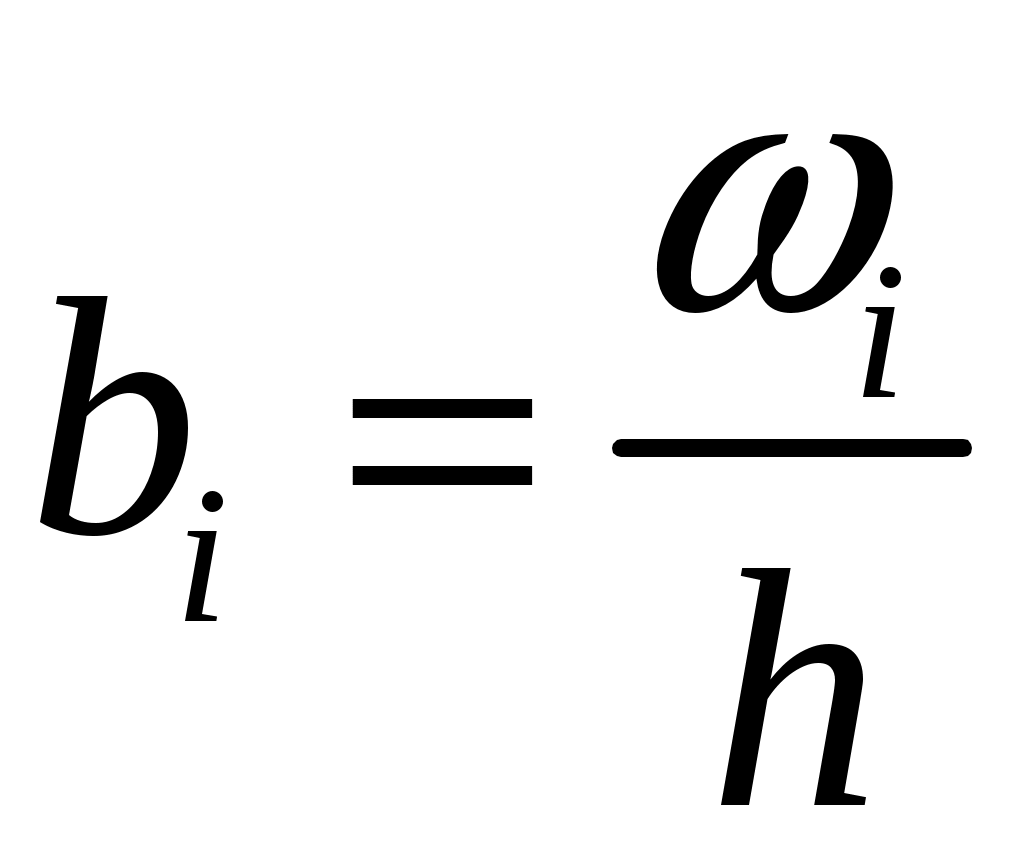 .
. 

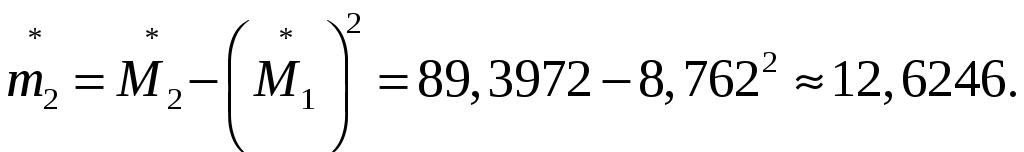
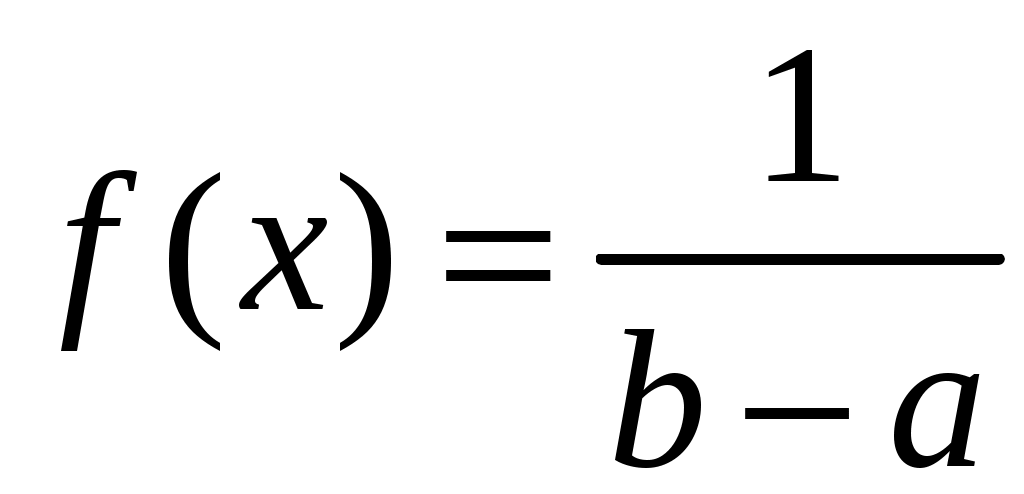 ,
,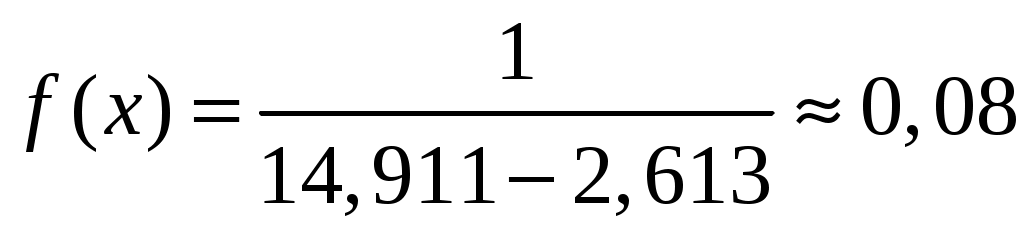 .
.