Контрольная работа по высшей математике. Решение Применим интегрирование по частям f4x3, f4, ge 2x, ge 2x 2 Тогда получаем

• Название: Решение Применим интегрирование по частям f4x3, f4, ge 2x, ge 2x 2 Тогда получаем
• Дата: 31.10.2022
• Размер: 62.9 Kb.
• Имя файла: Контрольная работа по высшей математике.docx
• Тип: Решение; #763775

Контрольная работа по высшей математике

Вариант 2

Группа 3сд-319

Тимофеевский Антон Сергеевич

Содержание

Задание 1 2

Задание 2 3

Задание 3 5

Задание 4 6

Задание 5 7

Список использованных источников 9

Задание 1

Условие:

Вычислить неопределенный интеграл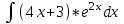
Решение:

Применим интегрирование по частям: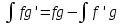



f=4x+3, f’=4, g’=e^2x, g=e^2x/2

Тогда получаем: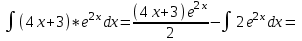



Сделаем замену переменных: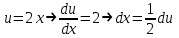



Тогда получаем: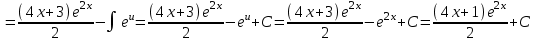


Ответ: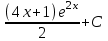

Задание 2

Условие:

Вычислить неопределенный интеграл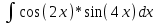
Решение:

Сделаем замену переменных: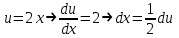



Отсюда: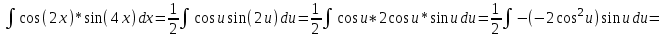



Сделаем замену переменных: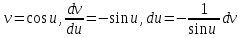



Тогда: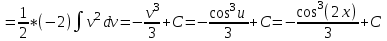


Ответ: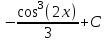

Задание 3

Условие:
Вычислить неопределенный интеграл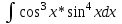
Решение: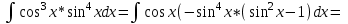



Сделаем замену переменных: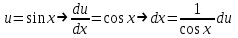



Тогда получаем: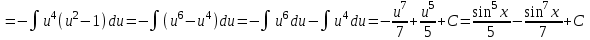


Ответ: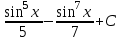

Задание 4

Условие:

Вычислить определенный интеграл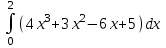


Решение: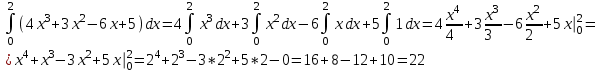


Ответ: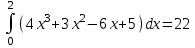

Задание 5

Условие:

Решить дифференциальное уравнение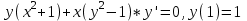


Решение:

Это дифференциальное уравнение имеет вид: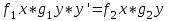



Где: f₁(x)= x, g₁(y)= y²−1, f₂(x)= −x²−1, g₂(y)=у

Приведём уравнение к виду:

g₁(y)/g₂(y)*y'= f₂(x)/f₁(x).

Разделим обе части уравнения на x и получим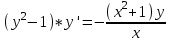



Разделим обе части уравнения на у, получим: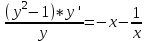



Этим самым мы разделили переменные x и y.

Теперь домножим обе части уравненния на dx,
тогда уравнение будет таким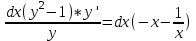



Возьмём от обеих частей уравнения интегралы: от левой части интеграл по y, от правой части интеграл по x.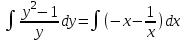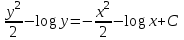





Отсюда выражаем у: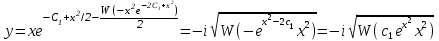



Найдем частное решение уравнения: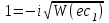



Отсюда с₁: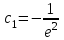

с

Подставляем в общее решение уравнения и получаем частное решение: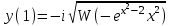


Ответ: ,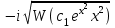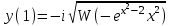

Список использованных источников

1. 
   Бугров, Я.С. Высшая математика в 3 т. Т.3 в 2 книгах. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учебник / Я.С. Бугров, С.М. Никольский. - Люберцы: Юрайт, 2016. - 507 c.
   
2. 
   Дорофеева, А.В. Высшая математика для гуманитарных направлений: Учебник для бакалавров / А.В. Дорофеева. - Люберцы: Юрайт, 2016. - 400 c.
   
3. 
   Шипачев, В.С. Высшая математика: Учебник и практикум / В.С. Шипачев. - Люберцы: Юрайт, 2016. - 447 c.