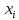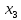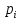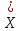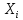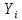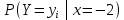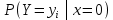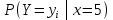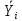Контрольная работа по ТВ. КР_ТВ_4 вар. Решение. Применим классическое определение вероятности число благоприятных исходов число всевозможных исходов
 Скачать 87.92 Kb. Скачать 87.92 Kb.
|
|
№ 4. В партии 5 исправных изделий и 2 бракованных. Наудачу взяты 4 изделия. Найти вероятность того, что среди них: а) одно бракованное; б) хотя бы одно бракованное; в) бракованных и небракованных поровну. Решение. Применим классическое определение вероятности: 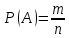 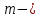 число благоприятных исходов; число благоприятных исходов;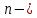 число всевозможных исходов; число всевозможных исходов;Всего в партии 7 изделий (5 исправных и 2 бракованных), из них берут 4 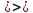 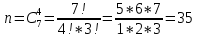 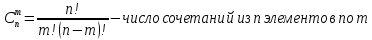 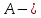 среди взятых изделий одно бракованное. среди взятых изделий одно бракованное.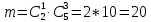 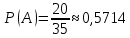 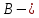 среди взятых изделий хотя бы одно бракованное. Искомую вероятность можно найти, отняв от единицы вероятность противоположного события: среди взятых изделий хотя бы одно бракованное. Искомую вероятность можно найти, отняв от единицы вероятность противоположного события: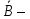 среди взятых изделий нет бракованных. среди взятых изделий нет бракованных.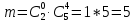 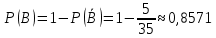 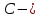 среди взятых изделий бракованных и небракованных поровну. среди взятых изделий бракованных и небракованных поровну.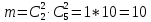 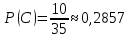 Ответ: 0,5714; 0,8571; 0,2857. №14. В задаче рассчитать надежность цепи. (Указаны вероятности работы элементов) 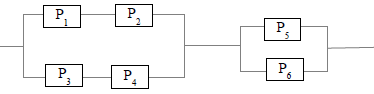 Решение. 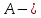 цепь надежна (схема работает). цепь надежна (схема работает).Разобьем цепь на два блока. Первый блок – элементы 1, 2, 3, 4; второй блок – элемент 5 и 6. Схема работает, если все оба блока надежны. 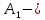 первый блок работает. первый блок работает.Разделим первый блок на два подблока: первый 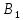 – элементы 1 и 2; второй – элементы 1 и 2; второй 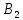 – элементы 3 и 4. Первый блок работает, если работает хотя бы один из его подблоков. – элементы 3 и 4. Первый блок работает, если работает хотя бы один из его подблоков.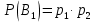 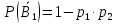 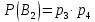 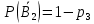 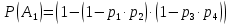 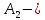 второй блок работает. второй блок работает.Второй блок работает, если работает хотя бы один из элементов 5 и 6. 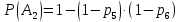 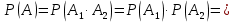 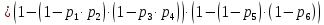 Ответ: 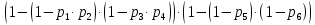 № 24. В магазин поступило 500 телевизоров, из них 200 отмечены знаком качества. Известно, что среди телевизоров со знаком качества 5% бракованных, а среди остальных телевизоров бракованных — 20%. а) Найти вероятность того, что случайно выбранный телевизор оказался бракованным. б) Случайно выбранный телевизор оказался бракованным. Найти вероятность того, что он имеет знак качества. Решение. 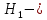 телевизор имеет знак качества. телевизор имеет знак качества. 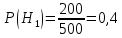 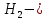 телевизор не имеет знака качества. телевизор не имеет знака качества. 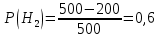 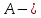 выбранный телевизор оказался бракованным. выбранный телевизор оказался бракованным.Условные вероятности этого события: 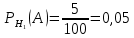 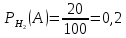 а) По формуле полной вероятности имеем: 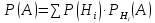 ; ;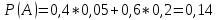 2) Вероятность того, что бракованный телевизор имеет знак качества, найдем по формуле Байеса: 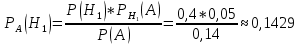 Ответ: 0,14; 0,1429. № 34. Вероятность того, что в заданный срок электрическая лампочка перегорит, равна 0,02 . В доме 300 лампочек. а) Какова вероятность того, что в доме в заданный срок перегорят ровно 4 лампочки? б) Какова вероятность того, что в доме в тот же срок перегорят не менее двух из них? Решение. 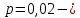 вероятность перегорания лампочки. вероятность перегорания лампочки.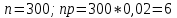 Так как 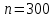 достаточно велико, а вероятность достаточно велико, а вероятность 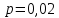 близка к нулю и близка к нулю и 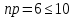 , то для вычисления требуемой вероятности, применим формулу Пуассона: , то для вычисления требуемой вероятности, применим формулу Пуассона: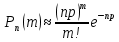 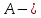 в заданный срок перегорят ровно 4 лампочки. в заданный срок перегорят ровно 4 лампочки. 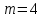 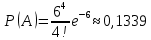 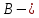 в заданный срок перегорит не менее двух лампочек. в заданный срок перегорит не менее двух лампочек. 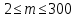 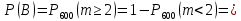 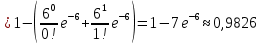 Ответ: 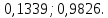 №44. Дискретная случайная величина 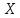 задана рядом распределения задана рядом распределения
Известно, что 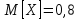 Найти 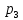 ; ; 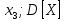 ; ;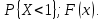 Начертить график Начертить график 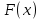 . .Решение. 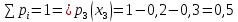 Математическое ожидание: 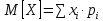 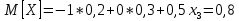 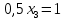 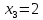 Ряд распределения примет вид:
Дисперсия: 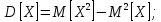 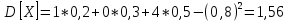 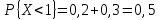 Найдем функцию распределения и построим ее график. 1) если 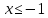 , то , то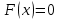 2) если 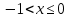 , то , то 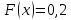 3) если 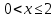 , то , то 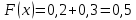 4) если 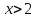 , то , то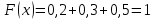 . .Функция распределения: 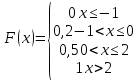 График функции распределения: 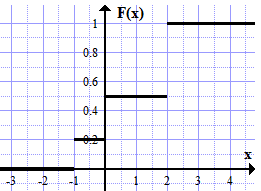 Ответ: 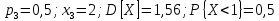 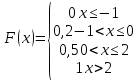 №54. Непрерывная случайная величина 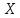 задана функцией распределения задана функцией распределения 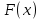 : : 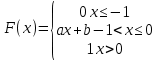 Найти: 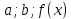 ; ; 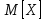 ; ; 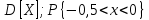 . .Начертить графики функции 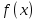 ; ; 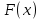 . . Решение. 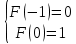 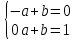 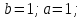 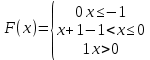 Плотность распределения: 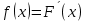 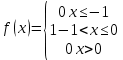 Математическое ожидание: 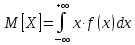 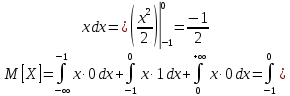 Дисперсия: 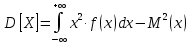 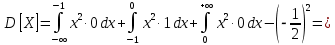 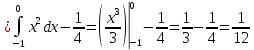 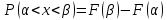 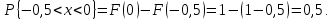 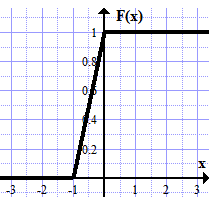 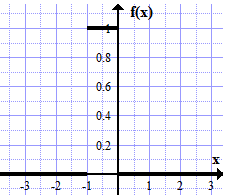 Ответ: 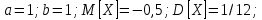 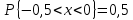 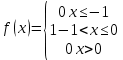 №64. Дана корреляционная таблица случайного вектора 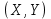
Найти 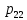 , зависимы , зависимы 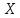 и и 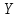 или нет, или нет, 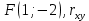 , линию регрессии , линию регрессии 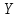 по по 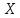 , составить уравнение линейной регрессии , составить уравнение линейной регрессии 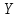 по по 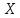 . Два последних графика изобразить на одной координатной плоскости. . Два последних графика изобразить на одной координатной плоскости.Решение. События 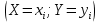 образуют полную группу событий, поэтому сумма всех вероятностей образуют полную группу событий, поэтому сумма всех вероятностей 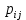 , указанных в таблице, должна быть равна 1. , указанных в таблице, должна быть равна 1.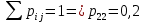 Закон распределения двумерной случайной величины 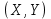 : :
Ряд распределения случайной величины 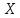 : :
Ряд распределения случайной величины 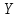 : :
Выясним, зависимы или нет события 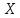 и и 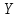 . .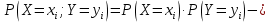 для независимых событий для независимых событий 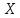 и и 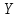 . .Так как: 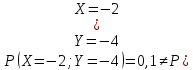 то величины 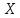 и и 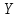 зависимы. зависимы.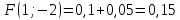 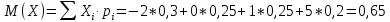 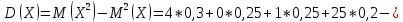 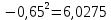 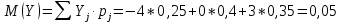 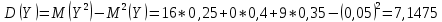 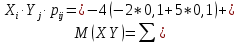 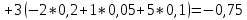 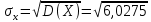 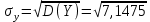 Корреляционный момент: 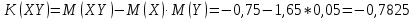 Коэффициент корреляции: 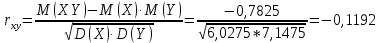 Для нахождения линии регрессии 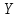 по по 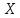 запишем условные законы распределения: запишем условные законы распределения:
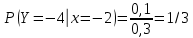 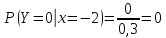 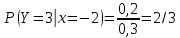 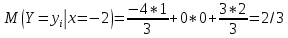
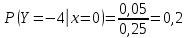 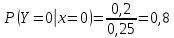 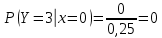 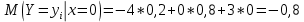
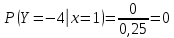 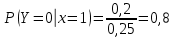 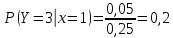 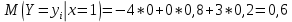
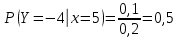 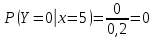 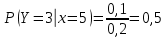 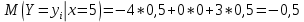
Уравнение линейной регрессии имеет вид: 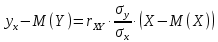 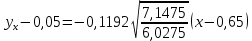 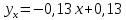 уравнение регрессии уравнение регрессии 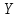 по по 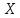 . .Построим эмпирические линии регрессии 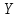 по по 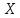 в виде ломаной, соединяющей точки в виде ломаной, соединяющей точки 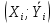 и уравнение регрессии и уравнение регрессии 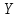 по по 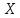 : : 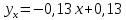 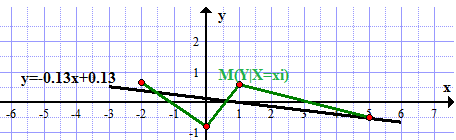 |