Плоская ферма. Плоская ферма_1. Решение Простая статически определимая ферма (рис. 1) составлена из n узлов и s
 Скачать 88.74 Kb. Скачать 88.74 Kb.
|
|
Определение реакций опор и сил в стержнях плоской фермы Дано: Р1 = 20 Н, Р2 = 10 Н, α = 45 , β = 45 , а = 1 м. Определитьусилия в стержнях фермы. 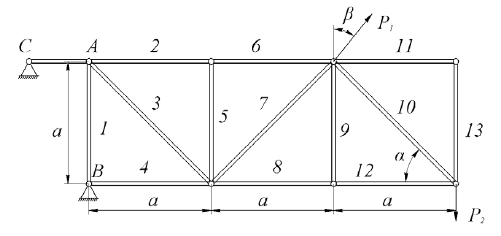 Рисунок 1- Простая статически определимая ферма Решение: Простая статически определимая ферма (рис. 1) составлена из n узлов и s стержней, число которых связано соотношением s = 2n – 3. Стержень 14 (СА) не принадлежит ферме, но с его помощью ферма крепится к опоре С, то есть для фермы стержень 14 является связью. В точке В ферма связана неподвижным цилиндрическим шарниром с другим телом. Поэтому, освободив ферму от связей, получим свободное твердое тело, на которое действуют активные силы P1 , P2 и силы реакций связей RA, XB, YB, причем RAнаправлена вдоль стержня СА, а XB, YB– параллельны осям координат (рис. 2 и 3). Определим эти неизвестные силы. Для этого, считая ферму абсолютно твердым телом, составим уравнение равновесия для системы сил, приложенных к ферме как для произвольной плоской системы сил: 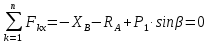 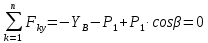 (1.1) (1.1)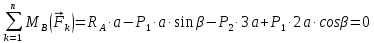 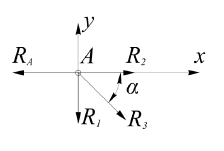 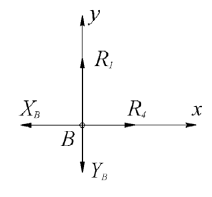 Рисунок 2 – Узел А Рисунок 3 – Узел В Из третьего уравнения системы (1.1) найдем 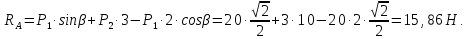 Из второго уравнения найдем YB: 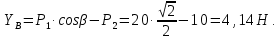 Из первого уравнения найдем XB: 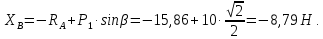 Усилия в стержнях найдем методом вырезания узлов. Для этого каждый раз будем вырезать тот узел, к которому приложено не более двух неизвестных усилий в стержнях фермы (ферма плоская). Таким узлом является узел В (рис. 3). Неизвестными являются усилия R1, R4 в первом и четвертом стержнях соответственно. Имеем плоскую систему сходящихся сил. Составим уравнения равновесия: 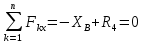 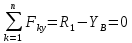 Решая эти уравнения относительно R1 и R4, получим: 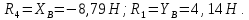 Теперь вырежем узел A. К этому узлу подходят три стержня – первый, второй и третий (рис. 2). Усилие в первом стержне определено из рассмотрения узла B. Таким образом, неизвестными усилиями являются усилия R2 и R3 в стержнях втором и третьем соответственно. Для определения этих неизвестных составим уравнение равновесия как для плоской системы сходящихся сил: 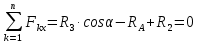 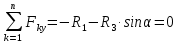 Откуда получим: 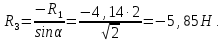 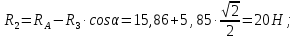 Вырежем узел III (рис. 4). 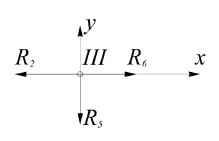 Рисунок 4 – Узел III Неизвестными являются усилия R5 и R6 в стержнях 5 и 6 соответственно. Уравнения равновесия: 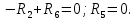 Откуда: 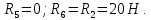 Вырежем узел IV. 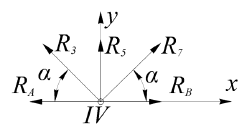 Рисунок 5 – Узел IV Неизвестными являются усилия R7 и R8 (рис. 5). Уравнения равновесия: 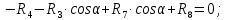 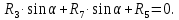 Oткуда 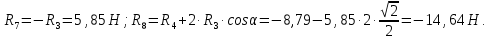 Вырежем узел VI (рис. 6). Неизвестными являются усилия R9 и R12. Уравнения равновесия 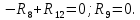 oткуда получаем: 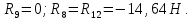 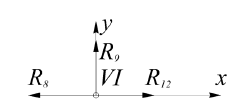 Рисунок 6 – Узел VI Вырежем узел V (рис.7). Неизвестными являются усилия R10 и R11. Уравнения равновесия 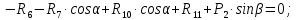 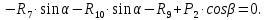 Oткуда 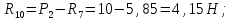 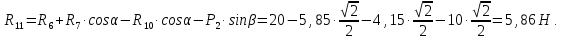 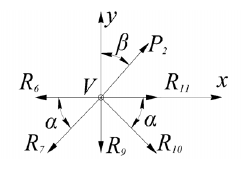 Рисунок 7 – Узел V Усилия в стержне 13 определим, вырезав узел VII (рис. 8). Уравнения равновесия 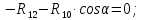 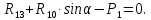 Из второго уравнения получим усилие в стержне 13: 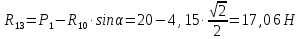  Рисунок 8 – Узел VII Из первого уравнения получим тождество, как то и должно быть, то есть: 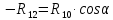 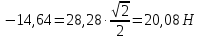 |
