Теория игр. Задание 7. Решение Проверим выполнение неравенства V(A B) V(A) V(B) V(1,2) V(1) V(2) 6000 5500 V(1,3) V(1) V(3)
 Скачать 15.66 Kb. Скачать 15.66 Kb.
|
|
Задание №7 Вариант 22 V(1) = 2500; V(2) = 3000; V(3) = 2500; V(1,2) = 6000; V(1,3) = 5800; V(2,3) = 6400; V(1,2,3) = 10000 Решение: Проверим выполнение неравенства V(A ∪ B) ≥ V(A) + V(B) V(1,2) ≥ V(1) + V(2) 6000 ≥ 5500 V(1,3) ≥ V(1) + V(3) 5800 ≥ 5000 V(2,3) ≥ V(2) + V(3) 6400 ≥ 5500 Так как равенство выполняется – делаем вывод что характеристическая функция является супераддитивной. V(1) + V(2) + V(3) < V(1,2,3) 8000 < 10000 Данное равенство также выполняется, поэтому игра является существенной. Значения заданной функции, выраженные в 0 – 1 редуцированной форме, будут иметь вид: V`(1) = V`(2) = V`(3) = 0; V`(1,2) = 6000-(2500+3000)/10000-(2500+3000+2500) = 0,25; V`(1,3) = 5800-(2500+2500)/10000-(2500+3000+2500) = 0,4; V`(2,3) = 6400-(3000+2500)/10000-(2500+3000+2500) = 0,45; V`(1,2,3) = 1 Для того, чтобы убедиться в непустоте С – ядра, следует проверить выполнение условий: 1) для одноэлементных коалиций V'(i) = 0 ≤ 1(3 – 1 +1 ) = 1/3; 2) для двухэлементных коалиций V'(1,2) = 0,25 ≤ 1/(3 – 2 +1 ) = 1/2; V'(1,3) = 0,4 ≤ 1/(3 – 2 +1 ) = 1/2; V'(2,3) = 0,45 ≤ 1/(3 – 2 +1 ) = 1/2; 3) для трехэлементных коалиций V'(1,2,3) = 1 = 1/(3 – 3 +1 ) = 1. Поскольку характеристическая функция игры, представленная в 0 – 1 редуцированной форме, удовлетворяет системе ограничений, то С - ядро такой системы не пусто, и, следовательно, любой дележ, принадлежащий С – ядру, является решением игры. В соответствии с теоремой о необходимых и достаточных условиях принадлежности дележа С – ядру, имеем: V'(1) = 0 ≤ х'1, V'(2) = 0 ≤ х'2, V'(3) = 0 ≤ х'3, V'(1,2) = 0,25 ≤ х'1 + х'2, V'(1,3) = 0,4 ≤ х'1 + х'3, V'(2,3) = 0,45 ≤ х'2 + х'3, V'(1,2,3) = 1 = х'1 + х'2 + х'3. Следует различать кооперативные игры с побочными платежами, в которых платежи являются переводимыми, и игры без побочных платежей, в которых платежи непереводимы. Рассмотренной системе ограничений будет удовлетворять вектор Х' = (х'1 = 0,3; х'2 = 0,3; х'3 = 0,4). Чтобы найти соответствующий ему вектор Х, воспользуемся взаимно однозначным соответствием множества всех дележей в эквивалентных играх, в соответствии с которым: х1 = k' х'1 + c'1 = [10000 – (2500 + 3000 + 2500)]·0,3 + 2500 = 3100, x2 = k' х'2 + c'2 = [10000 – (2500 + 3000 + 2500)]·0,3 + 3000 = 3600, x3 = k' х'3 + c'3 = [10000– (2500 + 3000 + 2500)]·0,4 + 2500 = 3300, Таким образом 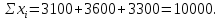 |
