Теория надежности, практическое 2. Практическое №2 (3). Решение P(t) e t P(120) e 120 8,810 4 1час f(t)(t)P(t)

• Название: Решение P(t) e t P(120) e 120 8,810 4 1час f(t)(t)P(t)
• Анкор: Теория надежности, практическое 2
• Дата: 04.01.2023
• Размер: 213.4 Kb.
• Имя файла: Практическое №2 (3).docx
• Тип: Решение; #872319

ПРАКТИЧЕСКОЕ 3АНЯТИЕ № 2.

Аналитическое определение количественных характеристик надёжности изделия.

Задачи:

1. Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течении 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час., а также среднее время безотказной работы.
P=0,9, t=120 час.
Решение:

P(t) = e^-λ*t

P(120)= e^-λ*120

λ=8,8*10^-4 1/час

f(t)=λ(t)*P(t)

f(t)=8,8*10^-4*0,9=7,92*10^-4

m_(t)=1/λ=1/8,8*10^-4=1136 час.
2. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час., частоту отказов для момента времени t=120 час и интенсивность отказов.
m(t)=640 час, t=120 час.

Решение:

m_(t)=1/λ

λ=1/640=1,56 *^10-3 1/час.

P(t) = e^-λ*t

P(120)= e^{—1,56*10-3*120}=0,42

f(120)=λ(120)*P(120)

f(120)=1,56*10^-3*0,42=0,65*10^-3 1/час


3. Время работы изделия подчинено нормальному закону с параметрами m_t = 8000 час., σ_t =1000 час. Требуется вычислить количественные характеристики надежности p(t) , f(t) , λ(t) для t=8000 час.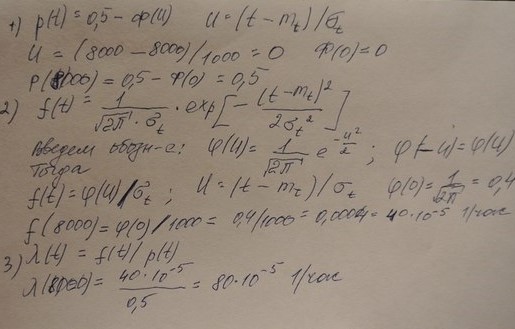



5. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами α=2,6 ; λ= 1,65*10^-7 1/час.
Требуется вычислить количественные характеристики надежности Р(t), f(t), λ(t) для t=150 час. и среднее время безотказной работы шарикоподшипников.



6.  Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено экспоненциальному закону. Требуется определить количественные характеристики надежности f(t), λ (t), m_t.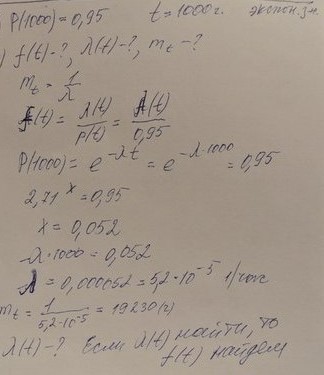



7. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено экспоненциальному закону. Необходимо найти его количественные характеристики надежности P(t), f(t), λ (t) для t=1000 час.

Дано: T=1260ч t=1000ч
p(t)-?
λ(t)-?
f(t)-?

Решение:
1)  -интенсивность отказа

2)Варианты безотказной работы





3) Частота отказов





8. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид f(t)=2e^-t (1-e^-t) . Необходимо найти количественные характеристики надежности P(t), λ (t), m_t.
Дано: f(t)=2e^-t (1-e^-t)
p(t)-?
λ(t)-?
m_t-?
Решение:

1) 

=1-2 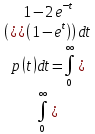 – вероятность безотказной работы на интенсивность времени от 0 до t

2)   интенсивность отказов изделия

 =  среднее время безотказной работы изделия


9. В результате анализа данных об отказах изделий установлено, что вероятность безотказной работы выражается формулой P(t)=3e^-t-3e^-2t+e^-3t.
Требуется найти количественные характеристики надежности P(t), λ (t), m_t.

Дано: f(t)=
p(t)-?
λ(t)-?
m_t-?
Решение:

1) 

2)



3)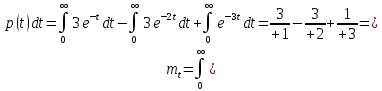 




10. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы m_t=1500 час. и среднее квадратическое отклонение σ_t = 100 час.

Дано: t=1300 ; m_t=1500 час;  

P-?; λ-?

Решение: по эксп. закону   ;   ;

По нормальному закону:   ;   ;

 ;   ; f(t)= 0,54*10^-4 1/час;

λ(t) = f(t)/P(t) = 0,0024 1/час