Занятие определение количественных характеристик надежности по статистическим данным об отказах изделия
 Скачать 327.5 Kb. Скачать 327.5 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1. Определение количественных характеристик надежности по статистическим данным об отказах изделия. Определение количественных характеристик надежности по статистическим данным об отказах изделия. Теоретические сведения Вероятность безотказной работы по статистическим данным об отказах оценивается выражением  (1.1) (1.1)где n(t) - число изделий, не отказавших к моменту времени t; N- число изделий, поставленных на испытания; P*(t) - статистическая оценка вероятности безотказной работы изделия. Для вероятности отказа по статистическим данным справедливо соотношение 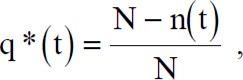 (1.2) (1.2)где N-n(t)- число изделий, отказавших к моменту времени t; q*(t) - статистическая оценка вероятности отказа изделия. Частота отказов по статистическим данным об отказах определяется выражением An(t) (1.3) N. At где An(t) - число отказавших изделий на участке времени (t, t+At); f*(t) - статистическая оценка частоты отказов изделия; At - интервал времени. Интенсивность отказов по статистическим данным об отказах определяется формулои An(t) 1.4) At • n(t)где n(t)- число изделий, не отказавших к моменту времени t; An(t) - число отказавших изделий на участке времени (t, t+At) ; i*(t)- статистическая оценка интенсивности отказов изделия. Среднее время безотказной работы изделия по статистическим данным оценивается выражением 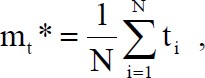 (1.5) (1.5)где ti - время безотказной работы i- го изделия; N- общее число изделий, поставленных на испытания; - статистическая оценка среднего времени безотказной работы изделия. Для определения по формуле (1.5) необходимо знать моменты выхода из строя всех N изделий. Можно определять из уравнения 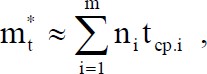 (1.6) (1.6)где - количество вышедших из строя изделий в 1- ом интервале времени; tcp.1 (ti-l+ti)/2 ; m—tk/At ; At—ti+l-ti ; ti-l -время начала i- го интервала; ti- время конца i- го интервала; tk - время, в течение которого вышли из строя все изделия; М-интервал времени. Дисперсия времени безотказной работы иэделия по статистическим данным определяется формулой Интенсивность отказов по статистическим данным об отказах определяется формулои An(t) 1.4) At • n(t)где n(t)- число изделий, не отказавших к моменту времени t; An(t) - число отказавших изделий на участке времени (t, t+At) ; i*(t)- статистическая оценка интенсивности отказов изделия. Среднее время безотказной работы изделия по статистическим данным оценивается выражением 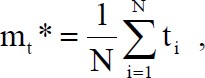 (1.5) (1.5)где ti - время безотказной работы i- го изделия; N- общее число изделий, поставленных на испытания; - статистическая оценка среднего времени безотказной работы изделия. Для определения по формуле (1.5) необходимо знать моменты выхода из строя всех N изделий. Можно определять из уравнения 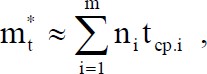 (1.6) (1.6)где - количество вышедших из строя изделий в 1- ом интервале времени; tcp.1 (ti-l+ti)/2 ; m—tk/At ; At—ti+l-ti ; ti-l -время начала i- го интервала; ti- время конца i- го интервала; tk - время, в течение которого вышли из строя все изделия; М-интервал времени. Дисперсия времени безотказной работы иэделия по статистическим данным определяется формулой (1.7) Dt E(t1 -т7)2 |
| Дћ,час. | | Дћ,час. | | Дћ,час. | |
| | | 30-35 | 4 | 60-65 | З |
| 5-10 | 5 | 35-40 | З | 65-70 | З |
| 10-15 | 8 | 40-45 | 0 | 70-75 | З |
| | 2 | 45-50 | | 75-80 | |
| 20-25 | 5 | 50-55 | 0 | | |
| 25-30 | 6 | 55-60 | 0 | | |
Решение. В данном случае
1
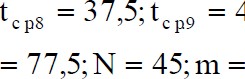
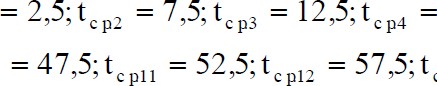
 7 5•t 22,5• t32,5• t42,5; ср1срб
7 5•t 22,5• t32,5• t42,5; ср1србt62,5• tср14ср.1б16. ср10ср1З
Используя формулу (1.6), получим
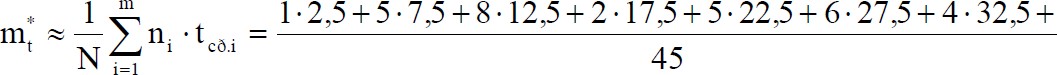
1
 427,5
427,545

Задача 1.7. На испытание поставлено 100 однотипньж изделий. За 4000 час. отказало 50 изделий. За интервал времени 4000 - 4100 час. отказало ещё 20 изделий. Требуется определить f*(t),i*(t) при €4000 час.
Задача 1.8. На испытание поставлено 100 однотипных изделий.
За 4000 час. отказало 50 изделий. Требуется определить p*(t) и q*(t) при €4000 час.
Задача 1.9. В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час. отказал еще один гироскоп. Требуется определить f*(t), i*(t) при t —1000 час.
Задача 1.10. На испытание поставлено 1000 однотипных электронных ламп. За первые 3000 час. отказало 80 ламп. За интервал времени 3000 - 4000 час. отказало еще 50 ламп. Требуется определить p*(t) и q*(t) при €4000 час.
Задача 1.11. На испытание поставлено 1000 изделий. За время t=1300 час. вышло из строя 288 штук изделий. За последующий интервал времени 1300-1400 час. вышло из строя еще 13 изделий. Необходимо вычислить p*(t) при €1300час. и t=1400 час.; f*(t), i*(t) при t —1300 час.
Задача 1.12. На испытание поставлено 45 изделий. За время t=60 час. вышло из строя 35 штук изделий. За последующий интервал времени 60-65 час. вышло из строя еще З изделия. Необходимо вычислить p*(t) при €60час. и t=65 час.; f*(t), i*(t) при t —60 час.
Задача 1.13. В результате наблюдения за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80-часовую приработку, получены данные до первого отказа всех 45 образцов, сведенные в табл. 1.2. Необходимо определить
Таблица 1.2.
| Дћ,час. | 11 | Дћ,час. | 11 | Дћ,час. | 11 |
| 0-10 | 19 | 30-40 | З | 60-70 | |
| 10-20 | 13 | 40-50 | 0 | | |
| 20-30 | 8 | 50-60 | | | |
Задача 1.14. На испытание поставлено 8 однотипньж изделий. Получены следующие значения ti (ti - время безотказной работы i-m изделия):
tl =560час.; е—700час.; t3 800час.; И—650час.; В=580час.; &760час.; е—920час.; «—850час. Определить статистическую оценку среднего времени безотказной работы изделия.
Задача 1.15. За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: tl =15мин.; е—20мин.; t3 =10мин.
И=28мин.; В=22мин.;
Требуется определить среднее время восстановления аппаратуры .
Задача 1.16. На испытание поставлено 1000 изделий. За время t=11000 час.
вышло из строя 410 изделий. Зв последующий интервал времени 11000-12000 час. вышло из строя еще 40 изделий. Необходимо вычислить p*(t) при t=11000 час. и t=12000 час. , а также f*(t), i*(t) при t=11000 час.

 — 5•10 5 1 час
— 5•10 5 1 час  343,3 час.
343,3 час.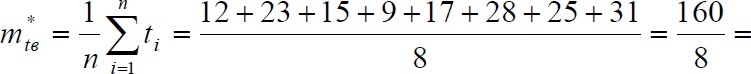 20 мин.
20 мин.