Решение. Пусть грузик отвис на некоторое расстояние х
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
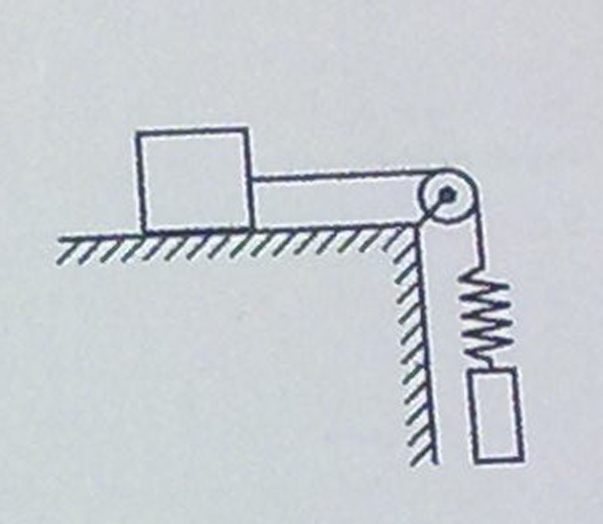
Брусок, покоящийся на горизонтальном столе, и маятник, состоящий из грузика и легкой пружины, связаны легкой нерастяжимой нитью, перекинутой через идеальный блок. Коэффициент трения между основанием бруска и поверхностью стола равен 0,2. Отношение массы бруска к массе грузика равно 8. Грузик маятника совершает колебания с периодом 0,5 с вдоль вертикали, совпадающей с вертикальным отрезком нити. Какова возможная амплитуда этих колебаний, при которой они остаются гармоническими?
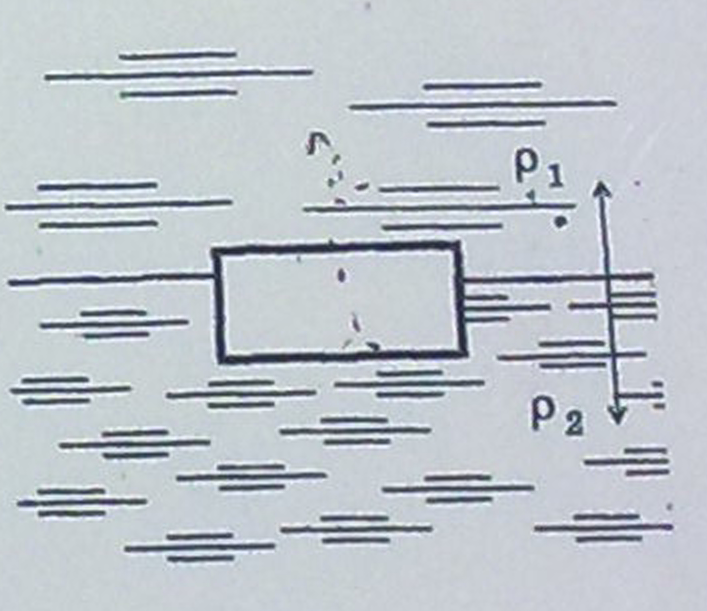
Решение. Пусть грузик отвис на некоторое расстояние х0, вычисляемое по закону Гука Колебания грузика остаются гармоническими, если совместно выполнены два условия. 1) Верхний конец пружины в процессе колебаний неподвижен. 2) Пружина и нить все время натянуты, поэтому грузик нигде не переходит в режим свободного падения. Из первого условия следует, что в крайнем нижнем положении грузика, когда удлинение пружины равно x0 + А, сила натяжения нити, равная по модулю упругой силе пружины, недостаточна для того, чтобы сдвинуть брусок: Fynp = k(x0 + А) = mg + kA ≤ μMg. Отсюда 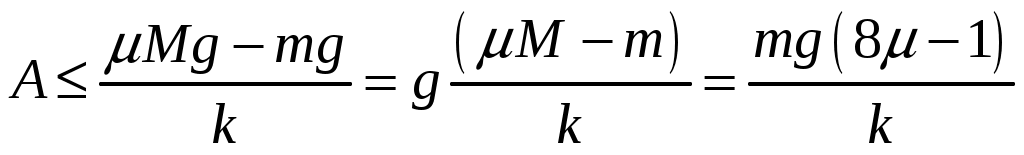 Жёсткость можно выразить из выражения для частоты пружинного маятника: 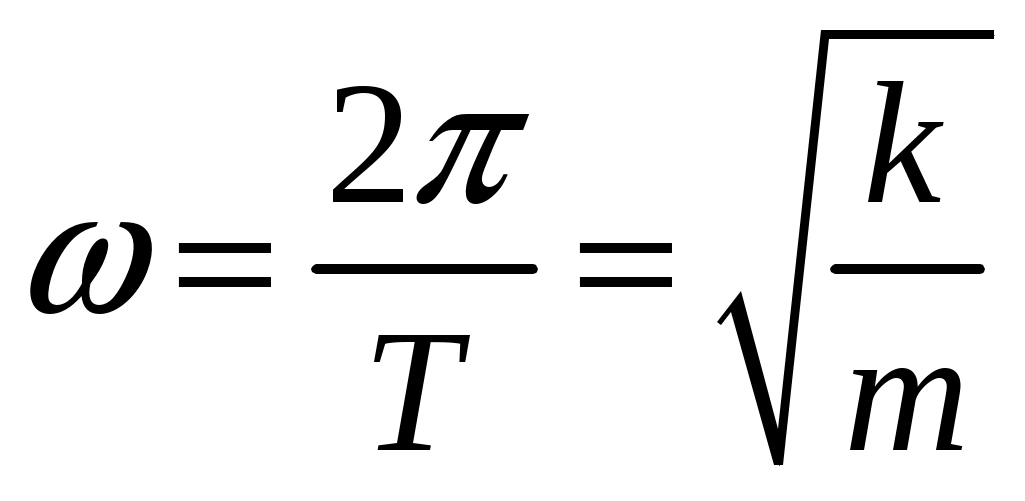 , откуда , откуда 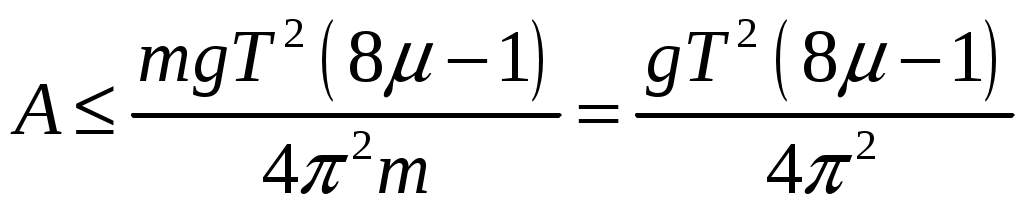 Проверим размерность: 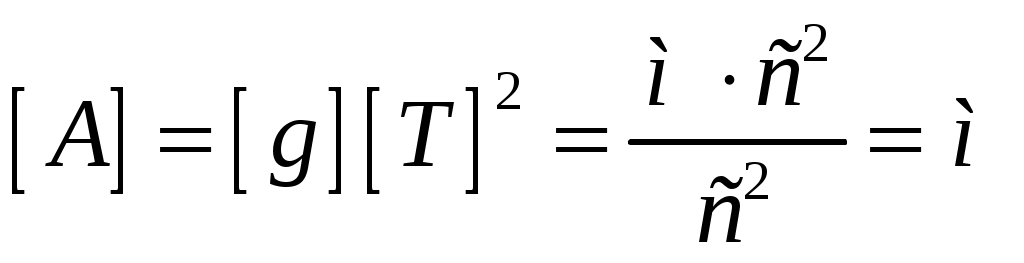 Вычислим: 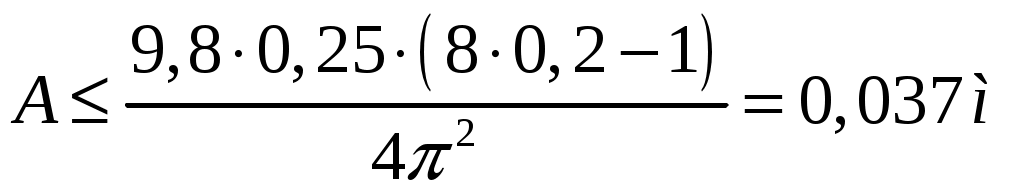 Ответ: Однородный брусок с площадью поперечного сечения 0,01 м2 плавает на границе несмешивающихся жидкостей с плотностями 800кг/м3 и 1000кг/м3 Пренебрегая сопротивлением жидкостей, определите массу бруска, если период его малых вертикальных колебаний равен
Решение. Применим метод аналогий. Подобно пружинному маятнику, этот брусок колеблется гармоническим образом под действием квазиупругой силы. В пружинном маятнике возвращающей силой является сила упругости, считаемая по закону Гука. В случае бруска это разность силы тяжести, действующей на поплавок, и силы Архимеда. Таким образом, дифференциальное уравнение таких колебаний будет 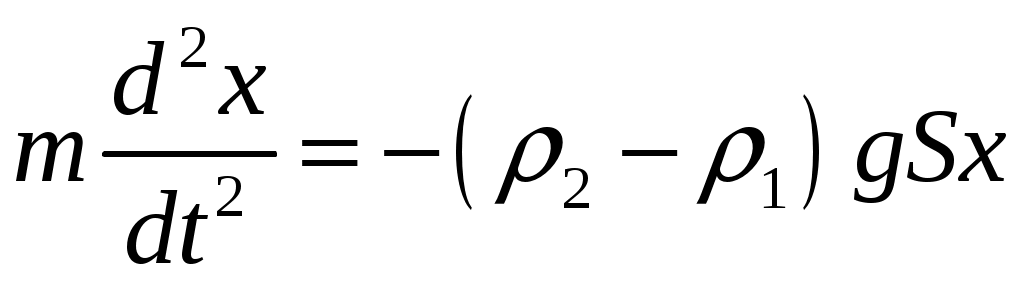 (нулевой уровень будем отсчитывать от точки, в которой сила тяжести уравновешена силой Архимеда). Решением этого уравнения будет (нулевой уровень будем отсчитывать от точки, в которой сила тяжести уравновешена силой Архимеда). Решением этого уравнения будет 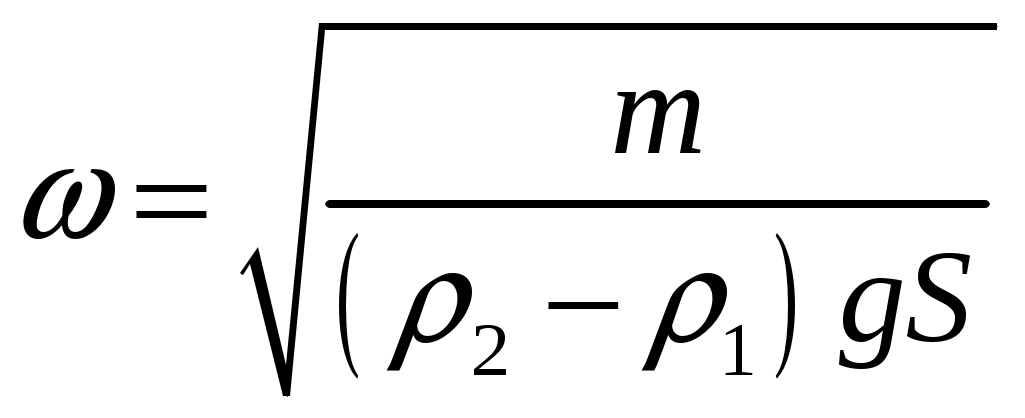 , аналогично колебаниям пружинного маятника. Так как , аналогично колебаниям пружинного маятника. Так как 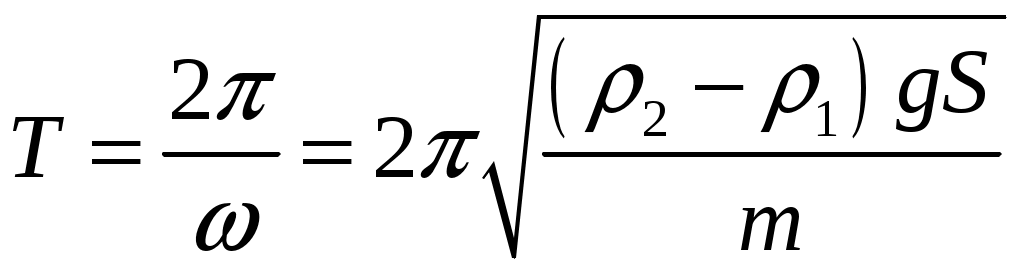 , откуда , откуда 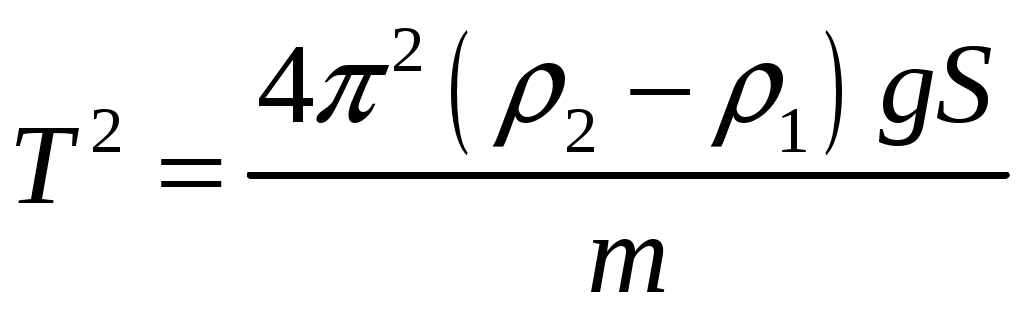 , откуда , откуда 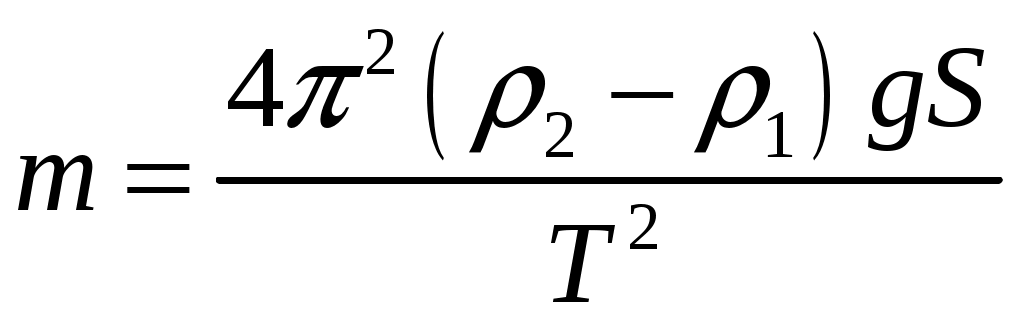 Проверим размерность: 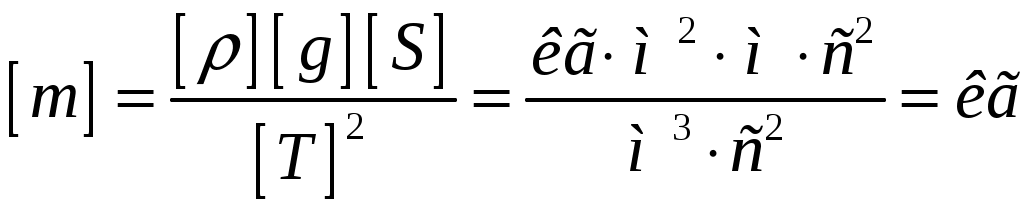 Вычислим: 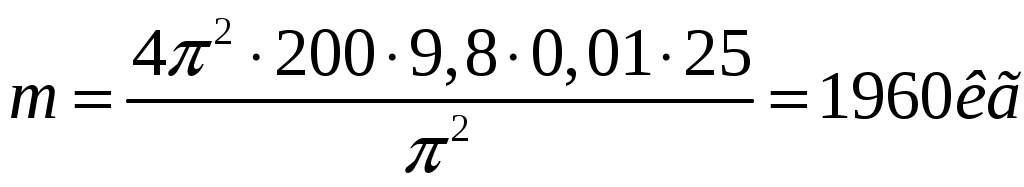 Ответ: Крылья пчелы, летящей за нектаром, колеблются с частотой 420 Гц, а при полёте обратно (с нектаром) ― 300 Гц. За нектаром пчела летит со скоростью 7 м/с, а обратно ― со скоростью 6 м/с. При полёте в каком направлении пчела сделает больше взмахов крыльями и на сколько, если расстояние от улья до цветочного поля 500 м.
Разницу числа взмахов найдём, вычтя например N2 из N1: 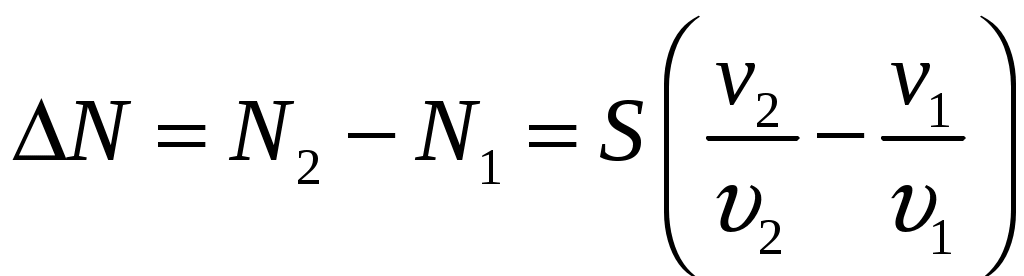 Проверим размерность: 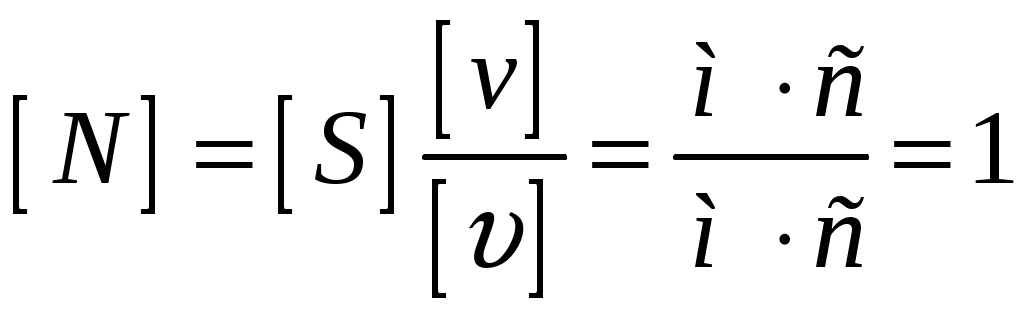 Вычислим: 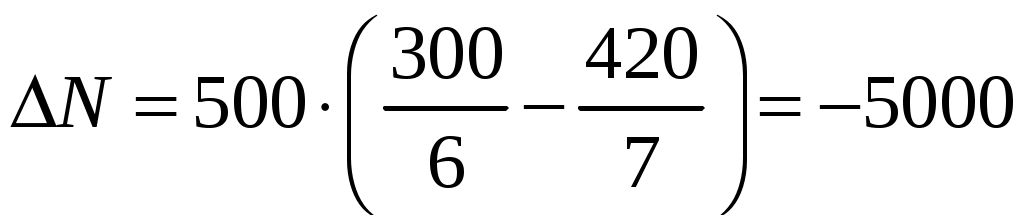 Ответ: на обратном пути пчела делает на 5000 колебаний меньше |