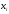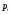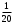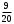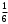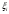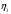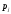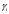Решение Пусть событие клиент выбрал банк по показателю стабильность банка
 Скачать 370.98 Kb. Скачать 370.98 Kb.
|
|
Клиент выбирает банк для получения ипотечного кредита по нескольким показателям: стабильность банка, процентная ставка, условия досрочного погашения кредита. Статистика показывает, что клиенты данного банка удовлетворены первым показателем с вероятностью 0,7, вторым – с вероятностью 0,6, третьим – с вероятностью 0,8. Какова вероятность того, что клиент, обратившийся в банк, будет удовлетворен: а) всеми тремя показателями; б) только двумя показателями; в) хотя бы одним из показателей? Решение: Пусть событие 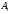 - клиент выбрал банк по показателю стабильность банка; - клиент выбрал банк по показателю стабильность банка;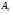 - клиент выбрал банк по показателю процентная ставка; - клиент выбрал банк по показателю процентная ставка;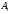 - клиент выбрал банк по показателю условия досрочного погашения. - клиент выбрал банк по показателю условия досрочного погашения.По условию задачи: 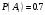 , , 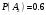 , , 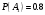 . .а) Пусть событие В – клиент выберет банк по всеми тремя показателями. 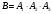 События 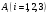 - независимые события, тогда по теореме о вероятности произведения независимых событий, получаем: - независимые события, тогда по теореме о вероятности произведения независимых событий, получаем: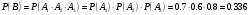 б) Пусть событие С – клиент выберет банк только по двумя показателями; 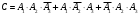 , где , где 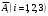 события противоположные событиям события противоположные событиям 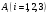 . .По теоремам о вероятности суммы и произведения событий, получаем: 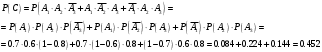 в) Пусть событие D – клиент выберет банк хотя бы одним из показателей. Рассмотрим противоположное событие 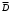 , противоположное событию D. , противоположное событию D.События D и 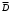 образуют полную группу событий, т.е. образуют полную группу событий, т.е. 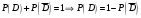 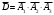 , где , где 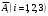 события противоположные событиям события противоположные событиям 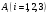 . .По теореме о вероятности произведения независимых событий, получаем: 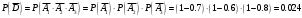 Тогда вероятность события D равна: 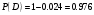 Ответ: а) 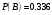 ; б) ; б) 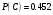 ; в) ; в) 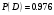 . .Для участия в студенческих отборочных соревнованиях выделено из первой группы курса 4 студента, 6 из второй, и 5 студентов из третьей. Вероятности того, что отобранный студент из первой, второй, третьей группы попадает в сборную института, соответственно равны 0,5, 0,4 и 0,2. Наудачу выбранный участник соревнований попал в сборную. К какой из указанных трех групп он вероятнее всего принадлежит? Решение: Пусть событие А – выбранный участник попал в сборную. Введем гипотезы: 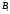 - выбран студент из - выбран студент из 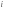 -оц группы -оц группы 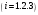 . .Всего 4+6+5=15 студентов. Тогда: 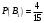 , , 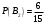 , , 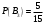 . .По условию задачи: 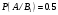 - вероятность того, что студент из первой группы попадет в сборную; - вероятность того, что студент из первой группы попадет в сборную;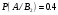 - вероятность того, что студент из второй группы попадет в сборную; - вероятность того, что студент из второй группы попадет в сборную;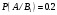 - вероятность того, что студент из третьей группы попадет в сборную. - вероятность того, что студент из третьей группы попадет в сборную.По формуле полной вероятности вероятность того, что выбранный студент попадет в сборную равна: 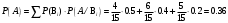 По формуле Байеса найдем вероятность того, что попавший в сборную студент был из 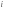 -ой группы -ой группы 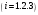 : :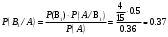 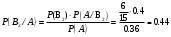 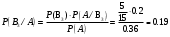 Видно что вероятнее всего студент, попавший в сборную, из второй группы. Ответ: 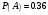 В стопке из 6 книг 3 книги по математике и 3 по информатике. Выбирается наудачу три книги. Составить закон распределения числа книг по математике среди отобранных. Найти ее математическое ожидание, дисперсию, среднее квадратическое отклонение, построить функцию распределения. Решение: Случайная величина Х - число книг по математике среди отобранных. Всего 6 книг 3 книги по математике и 3 по информатике. Найдем вероятности. 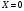 - среди отобранных книг нет книг по математике. - среди отобранных книг нет книг по математике.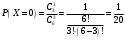 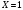 - среди отобранных книг одна книга по математике. - среди отобранных книг одна книга по математике.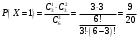 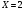 - среди отобранных книг две книги по математике. - среди отобранных книг две книги по математике.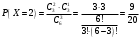 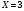 - среди отобранных книг три книги по математике. - среди отобранных книг три книги по математике.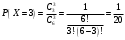 Закон распределения имеет вид:
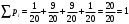 Найдем математическое ожидание: 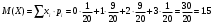 . .Найдем дисперсию: 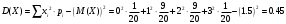 Найдем среднее квадратическое отклонение 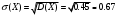 Составим функцию распределения и построим график: 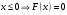 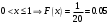 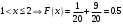 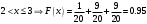 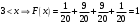 Тогда: 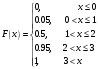 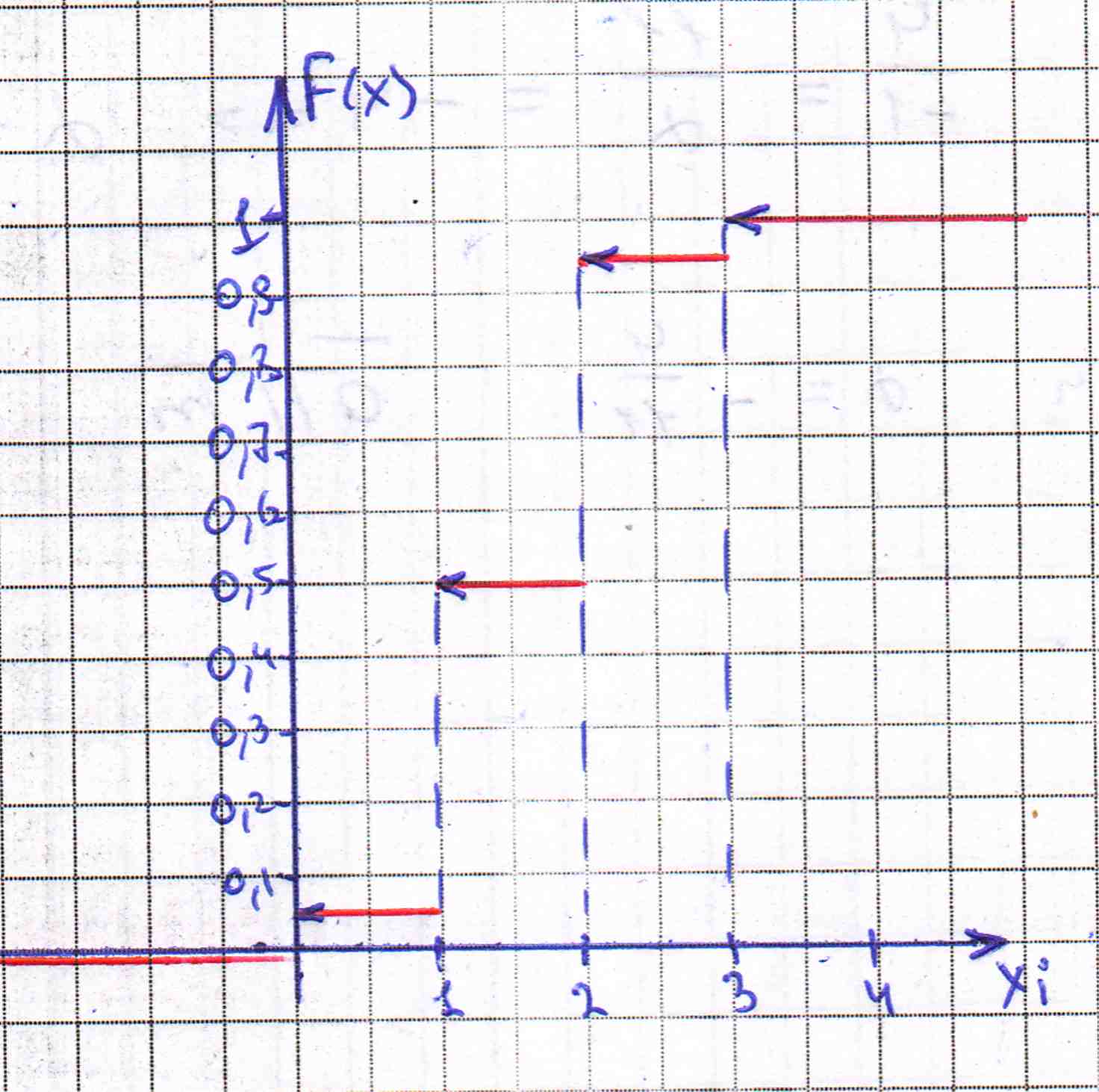 Случайная величина 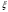 распределена по геометрическому закону с параметром распределена по геометрическому закону с параметром 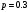 . Найти: . Найти:а) 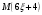 ; б) ; б) 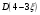 ; в) ; в) 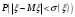 . .Решение: Т.к. случайная величина 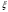 распределена по геометрическому закону, то распределена по геометрическому закону, то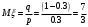 ; ; 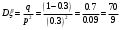 Тогда а) по свойству математического ожидания: 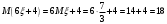 ; ;б) по свойству дисперсии: 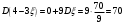 в) 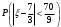 . .Функция распределения для геометрического распределения: 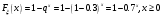 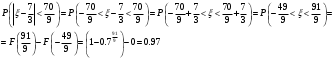 Ответ: а) 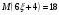 ; б) ; б) 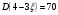 ; в) ; в) 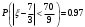 . .Случайная величина 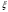 и и 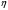 имеют следующий совместный закон распределения: имеют следующий совместный закон распределения: 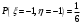 ; ; 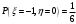 ; ; 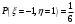 ; ; 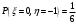 ; ; 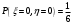 ; ; 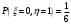 . .Выписать одномерные законы распределения случайных величин 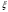 и и 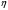 , вычислить математические ожидания , вычислить математические ожидания 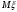 , , 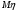 и дисперсии и дисперсии 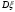 , , 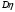 . .Найти ковариацию 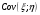 и коэффициент корреляции и коэффициент корреляции 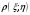 . .Выяснить зависимы или нет события 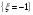 и и 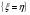 . .Составить условный закон распределения случайной величины 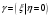 и найти и найти 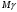 и и 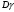 . .Решение: Сгруппируем исходные данные:
Выпишем одномерные законы распределения случайных величин 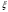 и и 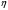 , ,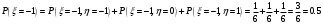 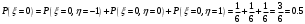 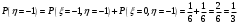 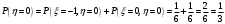 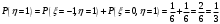 Законы распределения имеют вид:
Математические ожидания: 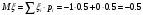 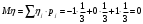 Дисперсии: 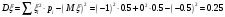 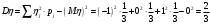 Найдем ковариацию 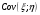 и коэффициент корреляции и коэффициент корреляции 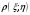 . .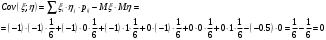 коэффициент корреляции 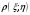 : :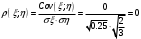 Выяснить зависимы или нет события 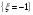 и и 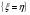 . .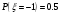 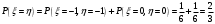 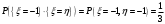 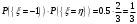 Т.к. 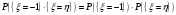 , то события , то события 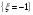 и и 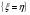 - независимы. - независимы.Составить условный закон распределения случайной величины 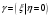 и найти и найти 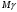 и и 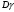 . .Найдем вероятности: 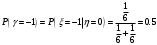 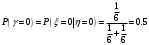 Закон распределения имеет вид:
Математические ожидания: 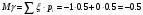 Дисперсии: 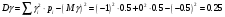 |