статья для сб. учителей. Решение Путь, который прошёл поезд можно представить по формуле
 Скачать 23.08 Kb. Скачать 23.08 Kb.
|
|
ОРГАНИЗАЦИЯ МАТЕМАТИЧЕСКИХ ОЛИМПИАД В 5 КЛАССЕ Н.А.Богуш,к.пед.н., доцент, ДВФУ, г.Уссурийск. Математические олимпиады уместно и необходимо использовать для осуществления воспитательной работы со школьниками. Олимпиады способствуют выявлению и развитию математических способностей учащихся. Одной из важнейших целей проведения математических олимпиадах по математике является развитие интереса учащихся к математике, привлечение учащихся к занятиям в факультативах и кружках. Проведение внеклассной работы по математике является прекрасным средством повышения деловой квалификации учителей. Для проведения школьной олимпиады необходимо подбирать задачи с учетом общего математического развития, качества математической подготовки учащихся класса или школы. Но занижать уровень задач ради обеспечения возможности награждения участников призом было бы неверно. Чтобы подготовить учащихся к участию в олимпиадах учителю приходится решать с ними задачи, похожие на те, что предлагаются на олимпиаде. Для этой цели мы предлагаем несколько задач с решениями по темам: задачи на составление уравнений ; задачи на время ; свойства чисел. Задачи на составление уравнений. Задача 1. От города 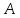 до города до города 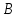 поезд шёл 16 часов. Обратный путь этот поезд прошёл со скоростью на 20 км в час большей и поэтому прошёл весь путь на 4 часа быстрее. С какой скоростью шёл поезд от поезд шёл 16 часов. Обратный путь этот поезд прошёл со скоростью на 20 км в час большей и поэтому прошёл весь путь на 4 часа быстрее. С какой скоростью шёл поезд от 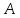 до до 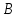 и чему равно расстояние от и чему равно расстояние от 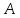 до до 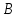 ? ? Решение:Путь, который прошёл поезд можно представить по формуле: 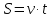 . Скорость поезда, с которой он ехал от . Скорость поезда, с которой он ехал от 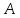 до до 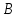 обозначим за обозначим за 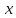 км в час. Известно, что от км в час. Известно, что от 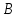 до до 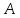 поезд шёл со скоростью на20 км в час быстрее, поэтому его скорость мы можем обозначить как поезд шёл со скоростью на20 км в час быстрее, поэтому его скорость мы можем обозначить как 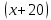 км в час. км в час. Обратный путь от 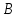 до до 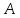 поезд прошёл за 12 часов, расстояние , которое он прошёл: поезд прошёл за 12 часов, расстояние , которое он прошёл: 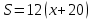 . А от . А от 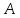 до до 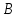 за 16 часов, значит путь, который прошёл поезд: . за 16 часов, значит путь, который прошёл поезд: .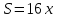 . .Записав формулы для расстояния и приравняв их, получим уравнение: 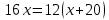 ; 16 ; 16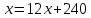 ; 16 ; 16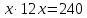 ; 4 ; 4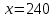 ; ; 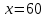 . .60 км в час скорость поезда, при прохождении расстояния от 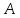 до до 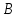 60  16 = 960 км расстояние от 16 = 960 км расстояние от 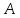 до до 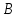 Ответ: 60 км в час, 960 км. Задача 2. У фермера было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Мальчик спросил фермера, сколько весит один поросёнок и один ягнёнок. Фермер ответил, что 3 поросёнка и 2 ягнёнка весят 22 кг, а два поросёнка и три ягнёнка весят 23 кг. Как узнать, сколько весит один поросёнок и сколько весит один ягнёнок? Решение: Обозначим вес 1 поросёнка – 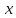 кг. ; вес 1 ягнёнка - кг. ; вес 1 ягнёнка - 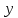 кг. 3 кг. 3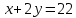 ; ; 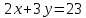 ; ; 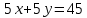 ; ; 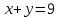 ; ; 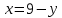 ; ; 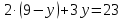 ; ; 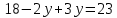 ; ; 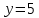 . .5 кг вес 1 ягнёнка. 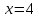 ; 4 кг вес 1 поросёнка. ; 4 кг вес 1 поросёнка.Ответ: 1 поросёнок – 4 кг, 1 ягнёнок – 5 кг. Задача 3. Четыре близнеца Коля, Петя, Боря и Вася праздновали свой день рождения. Им подарили коробку конфет. Договорившись разделить конфеты поровну, мальчики ушли играть с гостями. Коля зашел в комнату первым, взял свой долю и ушел. Через некоторое время зашел в комнату Петя взял четвертую часть конфет и ушел. То же самое проделали Боря и Вася, после чего в коробке осталась 81 конфета. Сколько всего конфет было в коробке, и сколько конфет взял каждый? Кто и сколько конфет должен взять еще? Решение: Так как осталась 81 конфета, то перед тем, как брал конфеты Вася, в коробке было 81 : 3  4 = 108 конфет; перед тем, как брал Боря: 108 : 3 4 = 108 конфет; перед тем, как брал Боря: 108 : 3  4 = 144 конфеты; перед тем, как брал Петя: 144 : 3 4 = 144 конфеты; перед тем, как брал Петя: 144 : 3  4 = 192 конфеты. Вначале было 192 : 3 4 = 192 конфеты. Вначале было 192 : 3  4 = 256 конфет. Каждому полагалось по 64 конфеты. Коля получил свою долю. Петя должен взять еще 16 конфет. Боря должен взять еще 28 конфет. Вася должен взять еще 37 конфет. 4 = 256 конфет. Каждому полагалось по 64 конфеты. Коля получил свою долю. Петя должен взять еще 16 конфет. Боря должен взять еще 28 конфет. Вася должен взять еще 37 конфет.Задача 4. У Андрея и Бори вместе 11 орехов, у Андрея и Вовы – 12 орехов, у Бори и Вовы – 13 орехов. Сколько всего орехов у Андрея, Бори и Вовы вместе? Решение: Ответ: 18 орехов. «Сложив» все три условия, получим, что удвоенная сумма орехов равна 36. Задачи на время. Задача 5. Имеются двое песочных часов на 7 минут и на 11 минут. Яйцо варится 15 минут. Как отмерить это время при помощи имеющихся часов? Решение: «Включим» одновременно двое часов. Когда 7 минутные часы пересыпятся, перевернём их и дадим сыпаться 4 минуты, до окончания пересыпания 11 минутных часов. Если теперь перевернуть 7 минутные часы, они будут сыпаться ровно 4 минуты, а всего часы сыпались 15 минут, что и требовалось. Задача 6. Вдоль беговой дорожки расставлено 12 флажков на одинаковом расстоянии друг от друга. Спортсмен стартует у первого флажка и бежит с постоянной скоростью. Уже через 12 секунд спортсмен был у 4 флажка. За какое время он пробежит всю дорожку? Решение: Между 12 флажками 11 «расстояний». Между 4 флажками 3 «расстояния». На пробег одного «расстояния» требуется 4 сек. Значит, всего потребуется 44 сек. Задача 7. Башенные часы отбивают три удара за 12сек. В течение, какого времени они пробьют шесть ударов? Решение: Поскольку 3 удара часы отбивают за 12 сек, интервал между двумя последовательными ударами составляет 6 сек. От первого удара до второго 6 сек и от второго до третьего тоже 6 сек. Шесть же ударов раздаются пятью интервалами. Следовательно, 6 ударов часы пробьют за 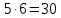 сек. сек.Задача 8. Я иду от дома до школы 30 мин, а мой брат 40мин. Через сколько минут я догоню брата, если он вышел из дома на 5 мин раньше меня? Решение: За 5 мин брат пройдёт 1/8 пути. За каждую минуту я прохожу 1/30 пути, а брат - 1/40, т.е. за минуту я навёрстываю (1/30-1/40) =1/120 часть пути. А 1/8 я наверстаю, соответственно, за (1/8):(1/120) = 15 мин, т.е. ровно на полпути до школы. Свойства чисел. Задача 9. Для двух натуральных чисел 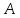 и и 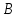 вычислили их сумму вычислили их сумму 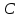 и произведение и произведение 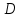 . Затем для чисел . Затем для чисел 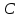 и и 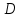 нашли их сумму нашли их сумму 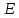 и произведение и произведение 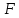 . Из чисел . Из чисел 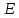 и и 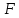 одно оказалось нечетным. Какое именно и почему? одно оказалось нечетным. Какое именно и почему?Решение: Ответ: 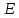 – нечетное число. – нечетное число.Первый способ. Пусть 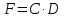 является нечетным числом, а является нечетным числом, а 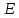 = =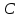 + +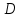 – четным. Тогда, числа – четным. Тогда, числа 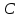 и и 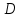 – оба нечетные. Но из того, что – оба нечетные. Но из того, что 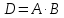 следует, что оба числа следует, что оба числа 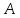 и и 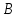 являются нечетными, а из того, что являются нечетными, а из того, что 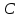 = =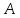 + +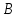 , следует, что числа , следует, что числа 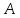 и и 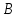 имеют разную четность, то есть получается противоречие. Если же предположить, что имеют разную четность, то есть получается противоречие. Если же предположить, что 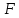 – четно, а – четно, а 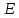 – нечетно, то получим, что числа – нечетно, то получим, что числа 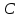 и и 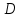 имеют разную четность, что возможно в случае, если числа имеют разную четность, что возможно в случае, если числа 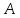 и и 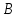 , в свою очередь, имеют разную четность. , в свою очередь, имеют разную четность. Второй способ: 1 случай :Если числа 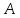 и и 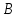 имеют разную четность, то их сумма имеют разную четность, то их сумма 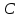 является нечетным числом, а произведение является нечетным числом, а произведение 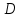 – четным,. Следовательно – четным,. Следовательно 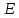 – нечетное число, а – нечетное число, а 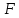 – четное. 2 случай : Если числа – четное. 2 случай : Если числа 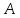 и и 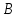 одновременно четные, то числа одновременно четные, то числа 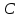 и и 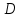 также являются четными, следовательно, числа также являются четными, следовательно, числа 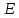 и и 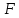 одновременно четные, что противоречит условию. 3 случай : Если числа одновременно четные, что противоречит условию. 3 случай : Если числа 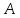 и и 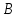 одновременно нечетные, то число одновременно нечетные, то число 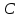 – четное и число – четное и число 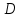 – нечетное, значит: – нечетное, значит: 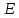 – нечетное, – нечетное, 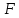 – четное. Следовательно, – четное. Следовательно, 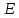 – нечетное число. Полное решение задачи : 7 баллов; дан верный ответ, но рассмотрены только два случая – 4 балла; дан верный ответ, но рассмотрен только один случай – 2 балла; дан верный ответ, но каждый из трех случаев рассмотрен только на конкретном примере – 3 балла; верный ответ дан на основе конкретных числовых примеров без рассмотрения различных случаев четности чисел – нечетное число. Полное решение задачи : 7 баллов; дан верный ответ, но рассмотрены только два случая – 4 балла; дан верный ответ, но рассмотрен только один случай – 2 балла; дан верный ответ, но каждый из трех случаев рассмотрен только на конкретном примере – 3 балла; верный ответ дан на основе конкретных числовых примеров без рассмотрения различных случаев четности чисел 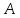 и и 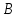 – 1 балл; ответ без обоснований или с неверными обоснованиями – 0 баллов. – 1 балл; ответ без обоснований или с неверными обоснованиями – 0 баллов.Задача 10. Сможете ли вы найти два числа, идущих подряд, у первого из которых сумма цифр равна 8, а второе делится на 8? Решение: У второго числа сумма цифр, скорее всего, будет 9 (поскольку у предыдущего 8). Попробуем искать среди чисел, одновременно кратных 9 (сумма цифр 9) и 8 (по условию), т.е. чисел, кратных 72. Первое же приходящее на ум такое число 72 годится, поскольку оно делится на 8, а у предыдущего 71 сумма цифр равна 8. Итак, это числа 71 и 72. Задача 11. Может ли число, составленное только из четвёрок, делиться на число, составленное только из троек? А на оборот? Решение: Например, 444444 делится на 33. Что же касается второй части задачи, то ответ всегда отрицательный. Так как какое бы число, составленное из троек, мы ни взяли, оно будет нечётным, следовательно, не может делиться ни на какое чётное число, в частности, и на составленное только из четвёрок. Список литературы 1. Агаханов Н.Х. Всероссийские олимпиады школьников по математике, 1993–2006. - М.:МЦНМО, 2007. —472с. 2. Агаханов Н.Х. Математика. Районные олимпиады. 6—11 классы. - М.: Просвещение, 2010.- 192 с. 3. Фарков А.В. Готовимся к олимпиадам по математике. – М.: Изд-во «Экзамен», 2007. - 157 с. |
