Семестровая работа №4 по аналитической динамике ЮУрГУ. Камалов А.В. П-329 Вариант№6 Задача №4. Решение Расчётная схема
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
 К  амалов А.В. П-329 , Вариант№6 амалов А.В. П-329 , Вариант№6Задача № 4. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБРАТНОЙ ФОРМЕ Условие задачи и варианты исходных данных Для одной из консервативных систем с двумя степенями свободы, изображенных в таблице 4.1 в положении равновесия, требуется: 1. Cоставить уравнения движения в обратной форме; 2. Определить собственные частоты и формы малых колебаний; 3. Проверить ортогональность собственных форм и изобразить их на графиках; 4. Найти законы движения во времени каждой из масс при свободных колебаниях системы с начальными условиями:  5. Изобразить найденный закон движения на графике, показать составляющие движения масс по каждой из собственных форм колебаний. Уравнения движения записать в обратной форме. При решении считать: а) положение равновесия устойчиво; б) массы являются точечными и могут перемещаться лишь в вертикальном направлении; в 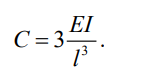 ) все участки стержня имеют одинаковую жесткость поперечного сечения EI и длину l; массы системы одинаковы: m1 =m2 =m; ) все участки стержня имеют одинаковую жесткость поперечного сечения EI и длину l; массы системы одинаковы: m1 =m2 =m; г) жесткость сосредоточенных упругих элементов и изгибная жесткость балок связаны: Решение: 1.Расчётная схема 2. Введём систему координат .Направим ось xгоризонтально , ось y – вертикально. 3.ЧСС 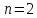 4 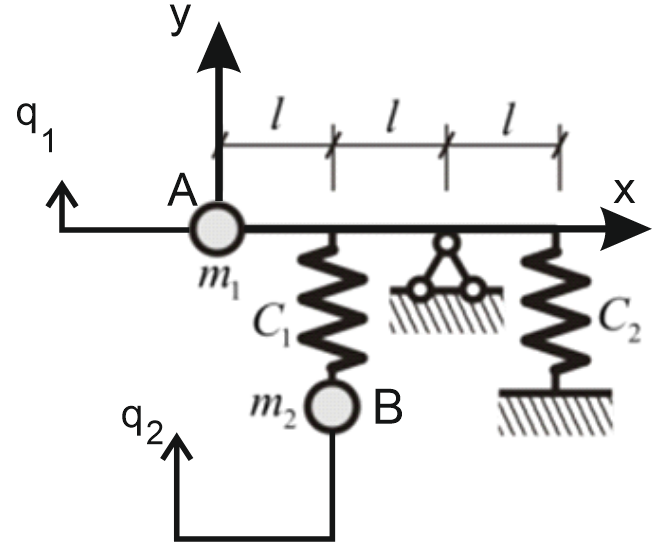 .Внедрим обобщённые координаты .Внедрим обобщённые координаты 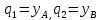 5.Уравнения движения Отклонения q1 и q2 точек А и В от положения статического равновесия можно рассматривать как результат деформирования упругих элементов под действием прикладываемых к механической системе сил. Так как упругие элементы полагаются невесомыми, то силами, действующими на механическую систему, являются силы инерции движения масс m1 и m2 , которые прикладываются в точках А и В. 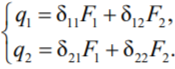 6 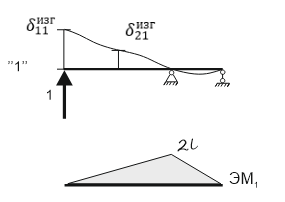 .Расчёт коэффициентов податливости .Расчёт коэффициентов податливости а)Изгибающая составляющая 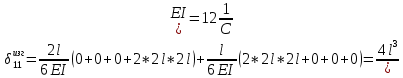 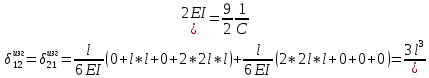 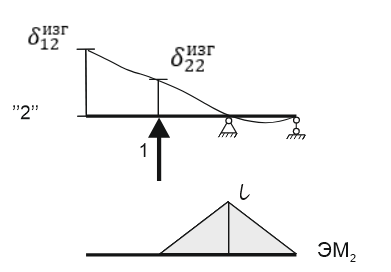 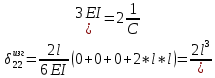 б)Пружинная составляющая 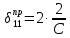  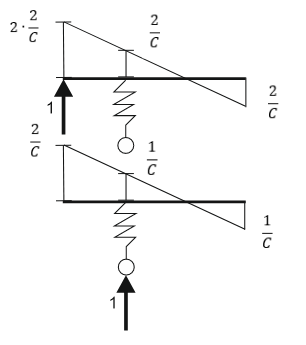 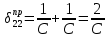  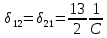 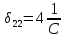 Подставим найденные коэффициенты податливости в уравнения движения 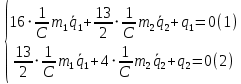 7.Собственные частоты и собственные формы Решением системы однородных дифференциальных уравнений второго порядка являются тригонометрические функции времени:  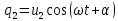  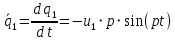 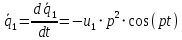 Для 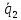 то же самое соотношение то же самое соотношениеПодставим данные соотношения в уравнения (1),(2) и сразу сократим на cos(pt) П   олучим: олучим: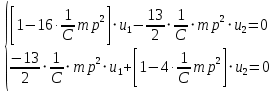 (3) (3)После замены получим :  (4) (4)Заметим ,что система (4) имеет нетривиальное решение, если определитель матрицы коэффициентов равен нулю : 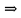 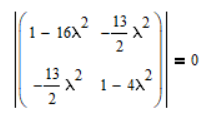 Решая данное уравнение , получим значения 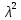 , и выберем из них ,корни которые больше нуля : , и выберем из них ,корни которые больше нуля : Отсюда 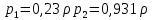 Соотношения амплитуд колебаний сосредоточенных масс на собственных частотах, то есть собственные формы, могут быть получены из любого уравнения системы (4). Воспользуемся, например, первым уравнением. Тогда: 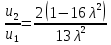   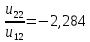   И матрицу собственных форм:  8.Проверка ортогональности собственных форм   В силу погрешности (появившейся из-за округления), ответ не стал полностью нулевым,но проверка сработала  И 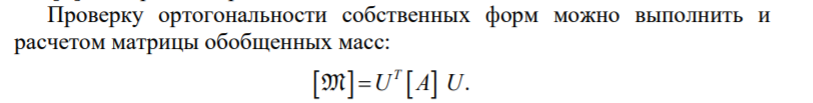 ли ли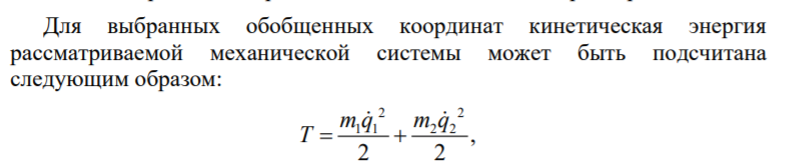  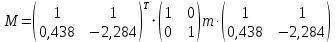 = = Элементы матрицы , не стоящие на главной диагонали , равны нулю , что подтверждает правильность решения системы. Чтобы определить амплитуду колебаний точки оси упругой балки в месте крепления упругого элемента С, следует учесть, что амплитуда колебаний массы m2 складывается из двух составляющих: первая составляющая вызывается деформацией балки, вторая – деформацией пружины: 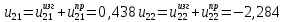 Удлинение пружины обусловлено действием силы инерции массы  : : Для первой собственной формы 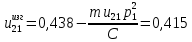 Аналогично на второй собственной форме  С 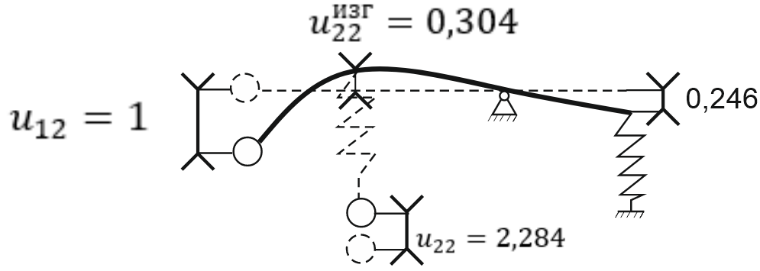  обственные формы механической системы показаны на рисунках обственные формы механической системы показаны на рисунках   9. Свободные колебания Закон изменения во времени обобщенных координат при свободных колебаниях, обусловленных заданием ненулевых начальных условий, получим разложением движения механической системы по собственным формам: 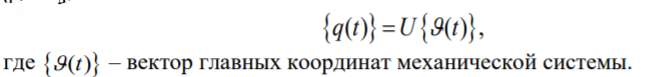 Для системы с двумя степенями свободы имеем 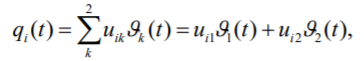 Определим главные координаты рассматриваемой расчетной схемы.  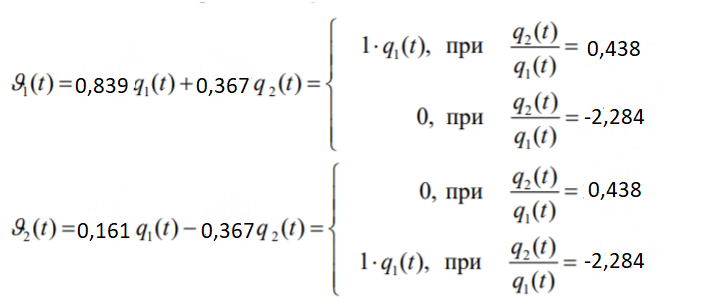   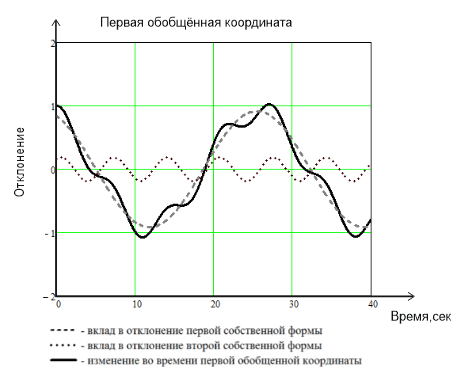  На графиках рис. а, б показаны изменения во времени обобщённых координат 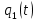 и и 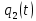 , ,а также составляющие перемещения каждой из масс в их движении по первой и по второй форме. , ,а также составляющие перемещения каждой из масс в их движении по первой и по второй форме. |
