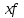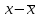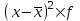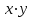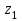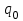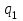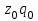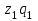Вариант 7 на 25.10.2021. Решение Рассчитываем средний процент годности продукции по трем партиям в целом или 92,2%
 Скачать 472.83 Kb. Скачать 472.83 Kb.
|
 Решение Рассчитываем средний процент годности продукции по трем партиям в целом: 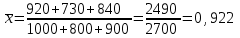 или 92,2% или 92,2%Рассчитываем средний процент брака продукции по трем партиям в целом: 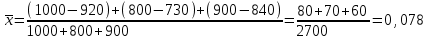 или 7,8% или 7,8%Рассчитываем по каждой партии продукции в отдельности определим долю годной продукции: - партия №1: 920/1000=0,920 или 92,0% - партия №2: 730/800=0,913 или 91,3% - партия №3: 840/900=0,933 или 93,3% Выводы: средний процент годности продукции по трем партиям в целом составляет 92,2%, а средний процент брака 7,8%. В партии № 1 оказалось 92,0% годной продукции, в партии № 2 – 91,3%, а в партии № 3 – 93,3%. Т.е. наибольший процент бракованной продукции в партии № 2, а наименьший процент брака в партии № 3.  Решение При выборе вида функции тренда можно воспользоваться методом конечных разностей (обязательным условием применения данного подхода является равенство интервалов между уровнями ряда). Конечными разностями первого порядка являются разности между последовательными уровнями ряда: Δ1t = Yt - Yt-1 Конечными разностями второго порядка являются разности между последовательными конечными разностями 1-го порядка: Δ2t = Δ1t - Δ1t-1 Конечными разностями j-го порядка являются разности между последовательными конечными разностями (j–1)-го порядка: Δjt = Δj-1t - Δj-1t-1 Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия.
Линейное уравнение тренда имеет вид y = bt + a Система уравнений МНК: an + b∑t = ∑y a∑t + b∑t2 = ∑y*t
Для наших данных система уравнений имеет вид: 11a + 66b = 490 66a + 506b = 3224 Из первого уравнения выражаем a и подставим во второе уравнение Получаем a = 29,055, b = 2,582 Уравнение тренда: y = 2,582 t + 29,055 Прогноз - на 2001г.: У2001=2,582*12+29,055=60,0 тыс.м2 - на 2002г.: У2002=2,582*13+29,055=62,6 тыс.м2 - на 2003г.: У2003=2,582*14+29,055=65,2 тыс.м2 Выводы: в среднем объем введеных жилых домов общей увеличился на 2,582 тыс.м2. При сохранении таких темпов роста в будущем объем введенных жилых домов в 2001г. составит 60,0 тыс.м2, в 2002г. 62,6 тыс.м2, в 2003г. – 65,2 тыс.м2.  Решение Для расчета показателей вариации составим вспомогательную таблицу1. Таблица 1-Вспомогательная таблица
Рассчитываем средний размер кредита по формуле средней арифметической взвешенной: 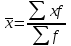 , , где 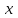 - индивидуальные значения осредняемого признака; - индивидуальные значения осредняемого признака;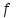 - это частота повторения признака. - это частота повторения признака. тыс.руб. тыс.руб.Определяем дисперсию по формуле: 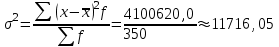 Так как была произведена 5% выборка договоров то именно эти 350 договоров создают выборочную совокупность. Это означает вся численность совокупности равняется N=350/0,05=7000 шт. Рассчитаем среднюю ошибку выборки для среднего размера кредита: 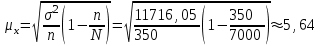 Рассчитываем граничную ошибку выборки. Коэффициент доверия t при заданной вероятности 0,954 равняется 2: 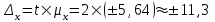 тыс.руб. тыс.руб. Таким образом, генеральная средняя составляет: 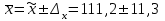 А это означает, что: 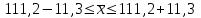 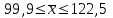 Выводы: с вероятностью 0,954 можно утверждать, что средний размер кредита находится в пределах от 99,9 тыс.руб. до 122,5 тыс.руб. Из общего числа кредитов, отобрали кредиты в размере 300 тыс. руб. и более. Их число составляет 34. Это означает, что доля таких кредитов в выборочной совокупности 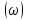 составляет: составляет: 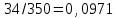 или 9,71%. или 9,71%.Тогда средняя ошибка выборки для доли 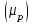 будет составлять: будет составлять: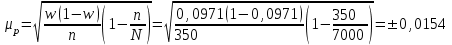 или или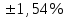 Коэффициент доверия t при заданной вероятности 0,954 равняется 2. Тогда граничная ошибка выборки при вероятности 0,954 для доли 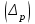 составляет: составляет: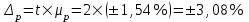 Итак, доля кредитов с размером 300 тыс. руб. и более во всей генеральной совокупности составляет: 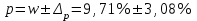 а это означает, что: 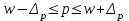 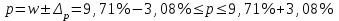 или или 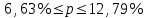 Выводы: С вероятностью 0,954 можно утверждать, что доля кредитов с размером 300 тыс.руб. и более в генеральной совокупности находится в пределах от 6,63% до 12,79%. 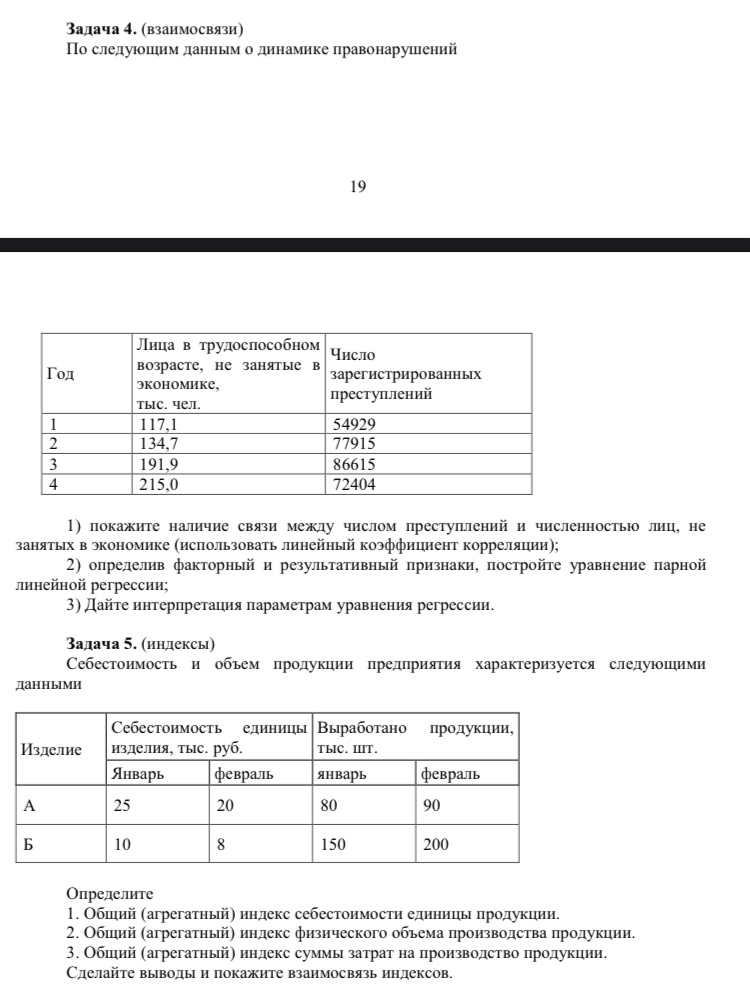 Решение Факторный признак - численность лиц, не занятых в экономике, результативный признак – число зарегистрированных преступлений. Представим зависимость между числом зарегистрированных преступление и численностью лиц, не занятых в экономике на графике (рис.1).  Рис.1 – Корреляционное поле зависимости числа преступлений от численности лиц, не занятых в экономике Для изучения зависимости между числом преступлений и численностью лиц, не занятых в экономике определим параметры линейного уравнения связи (уравнения регрессии по прямой) по формуле: 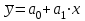 , , где 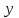 – значения результативного признака; – значения результативного признака; 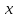 – значения факторного признака; – значения факторного признака;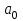 и и 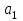 – параметры уравнения регрессии, которые определяют путем решения системы нормальных уравнений: – параметры уравнения регрессии, которые определяют путем решения системы нормальных уравнений: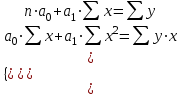 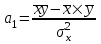 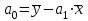 Промежуточные расчеты оформим в таблицу 1. Таблица 1-Рабочая таблица расчета промежуточных данных для определения значений уравнения регрессии
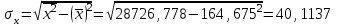 Найдем параметры уравнения регрессии: 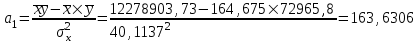 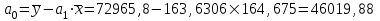 Итак, уравнение регрессии , которое описывает взаимосвязь между будет иметь вид: 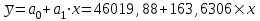 Вывод: с увеличением лиц в трудоспособном возрасте не занятых в экономике на 1 тыс.чел. приведет к увеличению числа зарегистрированных преступлений 163,6306 ед.  Решение Для удобства и простоты дальнейших расчетов составим рабочую таблицу 1, в которой укажем все необходимые промежуточные расчеты. Таблица 1-Рабочая таблица
Рассчитываем общий индекс затрат на производство продукции по формуле: 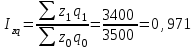 или 97,1% или 97,1% Рассчитываем общий индекс себестоимости по формуле: 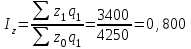 или 80,0% или 80,0% Рассчитываем общий индекс физического объема по формуле:  или 121,4% или 121,4% Выполним проверку рассчитанных общих индексов через взаимосвязь индексов:  Выводы: Физический объем производства продукции в феврале по сравнению с январем увеличился на 21,4% (121,4-100). Себестоимость продукции в феврале по сравнению с январем снизилась на 20,0% (80,0 -100), а затраты на производство продукции сократились на 2,9% (97,1-100). Список использованной литературы: 1. Годин, А. М. Статистика [Электронный ресурс]: учебник для студентов вузов, обучающихся по направлениям подготовки "Торговое дело", "Экономика", "Менеджмент" (квалификация "бакалавр") / А. М. Годин. - 11-е изд. - Москва : Дашков и К°, 2018. - 412 с. 2. Громыко, Г. Л. Теория статистики. Практикум [Электронный ресурс]: учебное пособие по дисциплине федерального компонента для студентов вузов, обучающихся по направлению подготовки 38.03.01 "Экономика" / Г. Л. Громыко. - 5-е изд., испр. и доп. - Москва : ИНФРА-М, 2019. - 238 с. 3. Дианов, Дмитрий Статистика финансов и кредита / Дмитрий Дианов. - М.: КноРус, 2018. - 247 c. Елисеева И.И. Статистика : учебник для академического бакалавриата - 5-е изд., перераб. и доп. - Москва : Издательство Юрайт, 2019. - 572 с. 5.Ефимова М.Р. Общая теория статистики. – М.: ИНФРА-М, 2019. – 413с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||