3.7 - 4.2 - 5.2 - 6.3 - 7.2 -ЗАКАЗ 57023. Задача 7 задача 2
 Скачать 155.5 Kb.
|
|
СОДЕРЖАНИЕ
Список использованных источников…………………………………………..…….. Задание 3.7 НУЖНЫ ОБНОВЛЕННЫЕ ДАННЫЕ По данным статистического ежегодника Гродненской области за последний год произведите группировку районов по числу родившихся, образовав не более четырех групп. Каждую группу и совокупность в целом охарактеризуйте числом районов, общим числом родившихся и общей численностью населения, рассчитайте число родившихся на 1000 жителей по каждой группе и по совокупности в целом. Сделайте вывод. Решение Используем данные статистического ежегодника Гродненской области за 2008 г. и группируем районы следующим образом:
*без учета г. Гродно Характеристика групп и совокупности в целом отображена в Таблице.
Проанализировав исходные данные, можно сказать, что число родившихся на 1000 жителей в крупных районных центрах выше. Это можно объяснить более высоким уровнем жизни и доходами населения. Задание 5.2 Имеются данные о распределении работников по возрастным группам в Гродненской области на конец 2006 г.
Рассчитайте средний возраст работника в Гродненской области в целом и отдельно по мужчинам и женщинам, сравните полученные результаты. Решение Определим границы варьирования рассматриваемой величины, т.е. возраста работников. В соответствии с Трудовым Кодексом, заключать трудовой договор можно с 16 лет. Пенсионный возраст для женщин составляет 55 лет, для мужчин – 60 лет. Т.е. нижний предел первого интервала равен 16, верхний предел последнего интервала – 60 лет.
Определим средний возраст работника в Гродненской области:  лет;Определим средний возраст работников мужского пола в Гродненской области:  лет;Определим средний возраст работников женского пола в Гродненской области:  года.Можно сделать вывод, что средний возраст работников достаточно высокий (39,6 лет) в Гродненской области. Средний возраст работников по гендерному признаку практически не отличается – 39,9 лет для мужчин против 39,3 года для женщин. Задание 6.3 По данным задачи 5.2. для всего населения рассчитайте: а) моду и медиану распределения работников по возрасту; б) показатели вариации возраста работников; в) ассиметрию распределения. Постройте график распределения и сделайте вывод об однородности и симметричности распределения. Решение а) Мода- это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту. В нашем случае, модальным является интервал 40-49 лет. В интервальном ряду распределения мода находим по следующей формуле:  ,где:  минимальная граница модального интервала, равна 40 лет; - величина модального интервала, равна 9 лет; частоты модального интервала, предшествующего и следующего за ним, равны соответственно 30,0; 25,6; 12,0.Следовательно, мода равна:  лет.Медиана - варианта, находящаяся в середине ряда распределения. В нашем случае, медианным является интервал 30-39 лет. В интервальном ряду распределения медиану рассчитываем следующим образом: 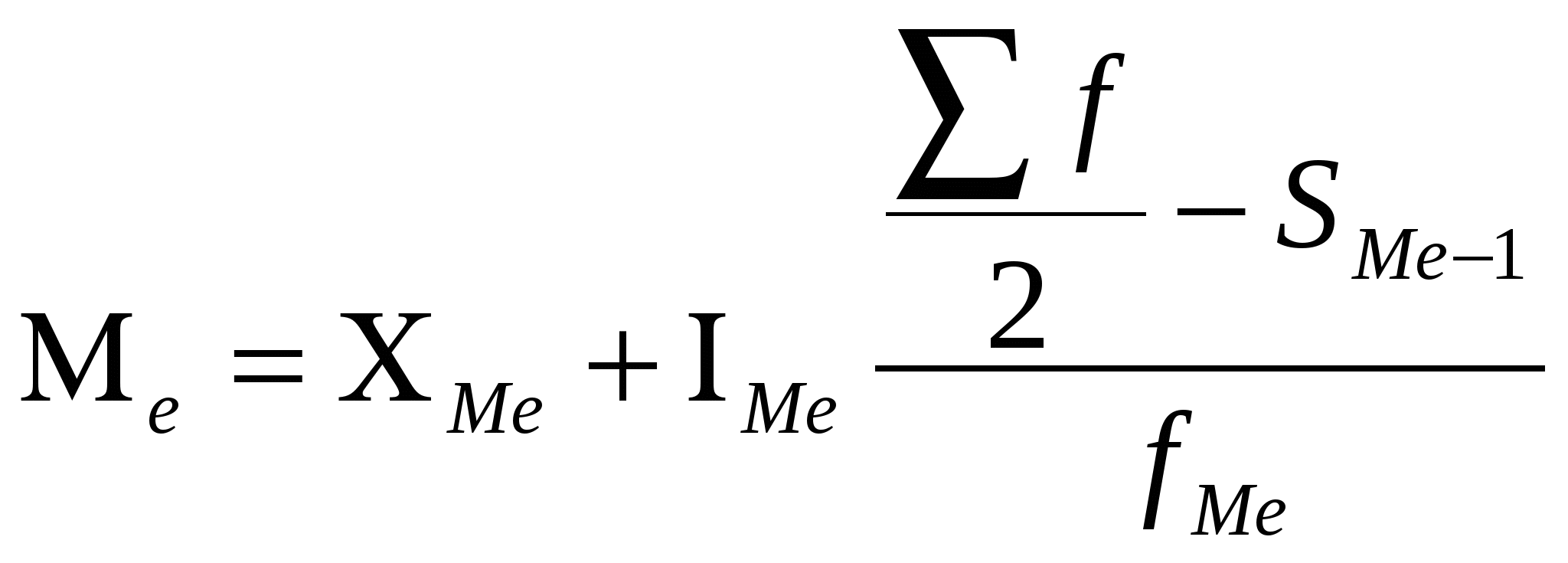 где:  - нижняя граница медианного интервала, равна 30 лет; - величина медианного интервала, равна 9 лет; - полусумма частот ряда, равна 50; - сумма накопленных частот, предшествующих медианному интервалу, равна (11,0+11,1)=22,1; - частота медианного интервала, равна 25,6.Таким образом, медиана равна:  лет.б) Абсолютные показатели вариации.
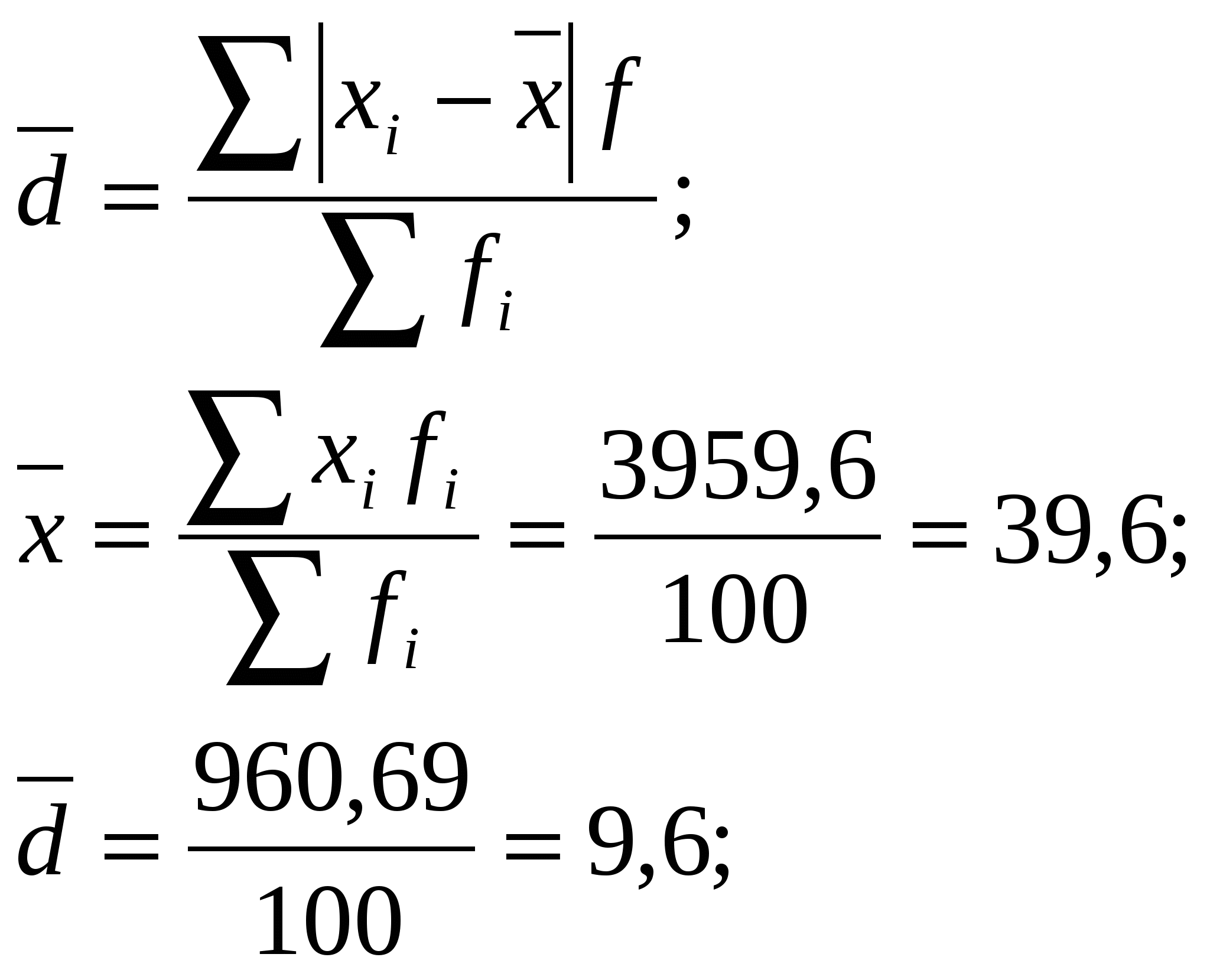
 Относительные показатели вариации.
 в) Коэффициент ассиметрии определяется следующим образом:  где  - центральный момент третьего порядка, равный   Так как As>0,5; то ассиметрия значительная. Построим график (гистограмму) распределения.  Можно сделать вывод, что имеет место однородное ассиметричное распределение. Задание 7.2 7.2. По данным задачи 5.2. предположив, что это результаты 4%-го выборочного обследования, определите для всего населения: 1) с вероятностью 0,954 предельную ошибку выборочного среднего и границы, в которых будет находиться средний возраст работников в генеральной совокупности; 2) с вероятностью 0,683 предельную ошибку выборки при определении доли и границы, в которых будет находиться удельный вес работников старше 50 лет. Решение
 где  - коэффициент доверия (критерий Стьюдента), при заданной вероятности 0,954   - дисперсия, равна 123,06; - размер генеральной совокупности, т.е. численность всех работников Гродненской области; по данным статистического ежегодника Гродненской области за 2008 г. численность трудовых ресурсов в 2006 г. составила 685 тыс. чел; - доля выборки ( ), отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности, равна 0,04 (из исходных данных); - число единиц выборочной совокупности,  работников.Следовательно, предельная ошибка для выборочной средней равна:  Определяем границы, в которых будет находиться средний возраст работников в генеральной совокупности - 
 где - коэффициент доверия (критерий Стьюдента), при заданной вероятности 0,683   - доля работников старше 50 лет, равна (12,0+10,3)=22,3%=0,223; - размер генеральной совокупности, т.е. численность всех работников Гродненской области; по данным статистического ежегодника Гродненской области за 2008 г. численность трудовых ресурсов в 2006 г. составила 685 тыс. чел; - доля выборки (), отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности, равна 0,04 (из исходных данных); - число единиц выборочной совокупности, работников.Следовательно, предельная ошибка для выборочной средней равна:  Определяем границы (в %), в которых будет находиться удельный вес работников старше 50 лет -  Список использованных источников
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||