4 задачи. Решение Рассмотрим движение центра масс стержня. В вертикальном положении он обладает потенциальной энергией, которая при падении переходит в кинетическую энергию вращения
 Скачать 89.71 Kb. Скачать 89.71 Kb.
|
|
КР1 -139. Тонкий однородный стержень длиной l из вертикального положения падает на горизонтальную поверхность. Найти линейные скорости крайней и средней точек стержня в момент времени, когда стержень займет горизонтальное положение.
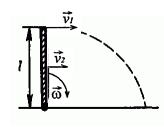 Рассмотрим движение центра масс стержня. В вертикальном положении он обладает потенциальной энергией, которая при падении переходит в кинетическую энергию вращения. Кинетическая энергия стержня в момент удара равна потенциальной: 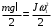 (1) (1)Момент инерции стержня относительно оси, проходящей через его конец, находим по теореме Штейнера: 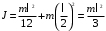 Подставим в формулу (1) и выразим угловую скорость в момент удара 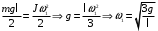 Линейная скорость стержня связана с угловой соотношением: 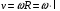 Угловая скорость всех частей стержня будет одинакова ω=ω1=ω2 Тогда скорость конца стержня в момент удара 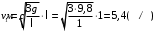 Скорость середины стержня 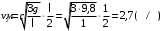 Ответ: v1=5,4 м/с; v2=2,7 м/с; КР2 -219. Два свинцовых шара с одинаковой массой движутся навстречу друг другу со скоростями v и 2v. Насколько увеличится температура шаров в результате их неупругого удара при v = 2,0 м/с?
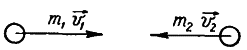 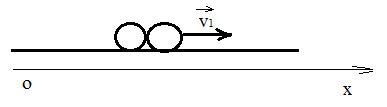 После неупругого удара шары будут двигаться как одно целое. При этом общую скорость шаров после удара можно определить из закона сохранения импльса: 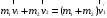 Или в проекции на ось ох и с учетом условия задачи (см рис): 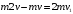 , отсюда , отсюда 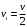 Изменение механической энергии шаров после удара: 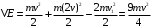 Эта же величина может быть выражена через удельную теплоемкость с и изменение температуры: 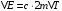 Тогда изменение температуры 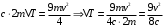 Удельную теплоемкость свинца находим в таблице с=130 Дж/кг·К 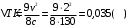 Ответ: ∆Т=0,035 К. 239. Кислород массой m = 1,0 кг, находящийся при давлении Р1 = 0,50 МПа и температуре Т1 = 400 К, изобарно расширяясь, увеличил объем в n = 2 раза, а затем сжимается изотермически до давления Р2 = 4,0 МПа. Найти суммарное приращение энтропии.
Приращение энтропии по определению равно 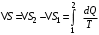 1)Газ совершает переход из состояния 1 в состояние 2 при постоянном давлении, поэтому изменение энтропии в переменных Т, V 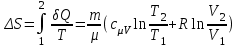 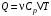 , где , где 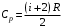 , для кислорода степень свободы молекул будем считать i=5, тогда , для кислорода степень свободы молекул будем считать i=5, тогда 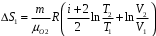 Из уравнения Гей Люссака 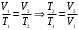 Тогда 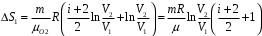 Изменение энтропии, учитывая, что процесс изотермический, 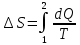 = =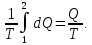 (1) (1)Согласно первому началу термодинамики, количество теплоты, полученное газом, Q = A + ∆U. Для изотермического процесса ∆U = 0, поэтому Q = A. Работа газа в изотермическом процессе 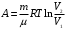 (2) (2)Подставив (2) в (1) найдем искомое изменение энтропии: 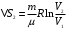 Общее изменение энтропии в обоих процессах 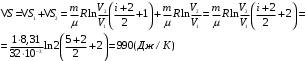 Ответ: ∆S=990 Дж/К. 259. Однородное электрическое поле напряженностью Е = 10 кВ/м образовано двумя заряженными параллельными пластинами (плоский воздушный конденсатор), расстояние между которыми d = 2,0 см. Между пластинами параллельно им помещается металлический лист толщиной d0 = 0,50 см. Найти напряжение между пластинами после внесения металлического листа.
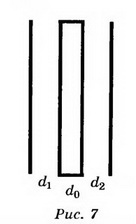 Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d1 и d2. Ёмкости этих конденсаторов: 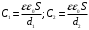 , где ε0 =8,85·10-12 Ф/м – электрическая постоянная, ε=1. , где ε0 =8,85·10-12 Ф/м – электрическая постоянная, ε=1.Эти конденсаторы соединены последовательно, поэтому их общая ёмкость 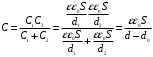 Электроемкость по определению равна 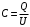 Тогда 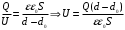 Заряд конденсатора найдем из формулы напряженности электрического поля между пластинами конденсатора: 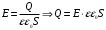 Тогда напряжение будет равно 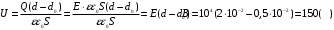 Ответ: U=150 В. |
