Билет 39 13960. Решение Рассмотрим линейную модель зависимости цены от факторов. На основе смысла переменных можно сделать следующие предположения о знаке влияния факторов а количество конкурирующих
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
 Решение: Рассмотрим линейную модель зависимости цены от факторов. На основе смысла переменных можно сделать следующие предположения о знаке влияния факторов: а) количество «конкурирующих» магазинов рядом знак отрицательный, поскольку чем больше магазинов, тем больше отток жителей в эти магазины, тем меньше должна быть цена в рассматриваемом магазине б) расстояние до ближайшей станции метро знак также отрицательный, поскольку чем дальше от метро, тем дальше идти. Соответственно, проще зайти за товаром в магазин, расположенный ближе к метро. Только более низкая цена в рассматриваемом магазине может привлечь жителей в) количество людей, проживающих «недалеко от магазина» здесь влияние положительное. Чем больше жителей, тем больше посетителей магазина. г) средняя цена в ближайших 5 магазинах знак также положительный, поскольку чем выше цена в соседних магазинах, тем выше ее можно поднять в рассматриваемом магазине д) крупная сеть или нет знак отрицательный, поскольку магазин может позволить себе приобретать товары большими партиями, следовательно, с большой скидкой. В результате может снизить цену для привлечения покупателей. Выполним анализ ситуации с помощью среды Matrixer. Создадим в Matrixer 6 новых переменных: Y - цена товара X1 – количество «конкурирующих» магазинов рядом X2 – расстояние до ближайшей станции метро X3 – количество людей, проживающих «недалеко от магазина» X4 – средняя цена в ближайших 5 магазинах X5 – крупная сеть или нет Скопируем из файла заданий Excel исходные данные. Оценим параметры линейной регрессионной модели. Для этого в командном окне пишем Y: 1 X1 X2 X3 X4 X5 После ввода команды в командное окно нажимаем кнопку Выполнить. В результате получаем окно с результатами вычислений: 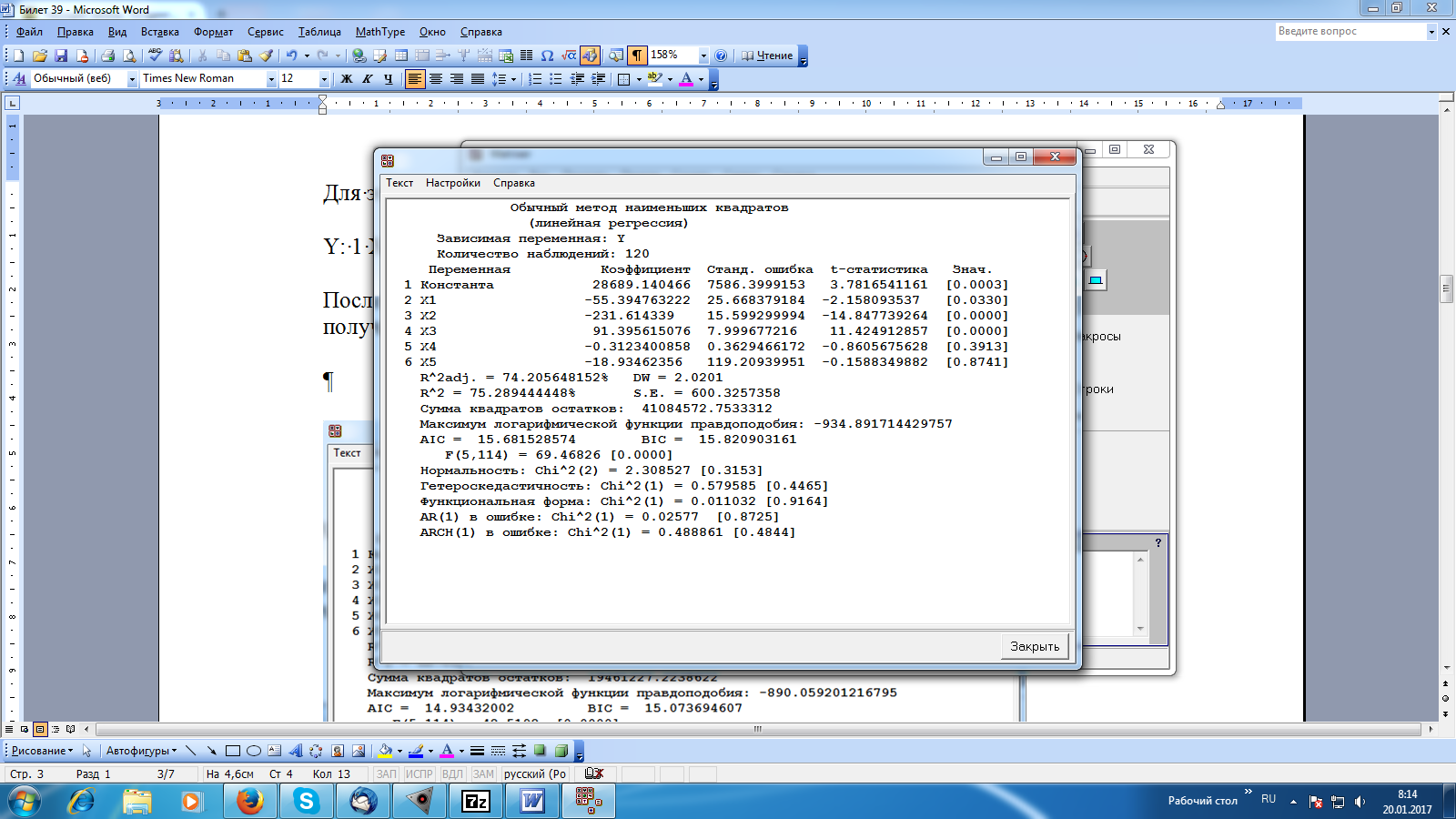 Верхняя часть полученной таблицы содержит общую информацию об уравнении: тип уравнения (линейная регрессия), метод оценивания (обычный МНК), использованное в оценке количество наблюдения (120 в данном случае). Вторая часть таблицы содержит непосредственно оценки параметров при каждом факторе, их стандартные ошибки, t-статистики для проверки гипотез о равенстве нулю каждого коэффициента, и соответствующие РДУЗ (в таблице — «Знач.»). Последний блок результирующей таблицы содержит дополнительные статистики, касающиеся оценок уравнения. Получаем уравнение: Y=28689,14-55,395X1-231,614X2+91,396X3-0,312X4-18,935X5 Сравнивая знаки коэффициентов с предварительным анализом, делаем вывод, что только предположение по переменной X4 оказалось ошибочным. Основываясь на информации второго блока, мы уже можем начать проверку качества исследуемой модели, а именно — проверку значимости отдельных коэффициентов. В частности, видно, что РДУЗ напротив 4 факторов достаточно мал, т.е. составляет менее любого из стандартных приемлемых уровней допустимой вероятности ошибки первого уровня — 0.1, 0.05 и даже 0.01 для трех коэффициентов. Для факторов X4 (средняя цена в ближайших 5 магазинах) и X5 (крупная сеть или нет) ситуация обратная: РДУЗ достаточно велик, чтобы сделать вывод о их незначимости. Значения коэффициентов при переменных (при значимых факторах) говорят о направлении и силе их влияния. Согласно форме уравнения (линейная регрессия) мы можем сделать предварительное заключение, что, например, чем больше жителей живет недалеко от магазина, тем выше изучаемая цена на товар (в среднем — приблизительно 91,396 рубля на каждую тысячу человек), тогда как большее число конкурентов и близость к метро отрицательно сказываются на цене (на каждого конкурента цена на товар становится меньше в среднем на 55,395 руб., в магазинах, располагающихся ближе к метро — выше приблизительно на 231,614 руб. на каждые 100 метров. Подобных выводов о влиянии на цену факторов X4 (средней цены в ближайших 5 магазинах) и X5 (магазинов, принадлежащих крупной торговой сети), сделать нельзя, т.к. влияние этих факторов признано незначимым. Последний блок результирующей таблицы содержит дополнительные статистики, касающиеся оценок уравнения. Наибольший интерес в этой части таблице представляют строки Нормальность, Гетероскедастичность, Функциональная форма. В этих строках приведены результаты расчетов критериев проверки, соответственно, нормальности остатков, гомоскедастичности остатков, линейной функциональной формы. Форма результата расчета по критериям — вполне стандартная: приведен тип статистики (Chi^2(1) — статистика типа Хи-квадрат с 1 степенью свободы), значение статистики (расчетное значение функции отклонения) и РДУЗ (в квадратных скобках после значения статистики). Рассмотрим, например, результат проверки на нормальность остатков в модели. Основная гипотеза состоит в том, что остатки действительно являются реализацией нормально распределенной случайной величины, РДУЗ составил более 0,3, т.е. гипотезу отвергнуть не удается (стандартным уровнем допустимой вероятности ошибки первого рода в таком критерии можно смело считать 0.05, что существенно ниже достигнутой значимости). Таким образом, мы можем сделать вывод, что остатки можно признать нормально распределенными. Аналогично мы делаем вывод о том, что определить гетероскедастичность в модели не удалось, однако форму модели можно считать линейной. Поскольку в модели имеются незначимые факторы, имеет смысл исключить их и построить новое уравнение регрессии. Исключим сначала фактор X5 как наименее значимый: 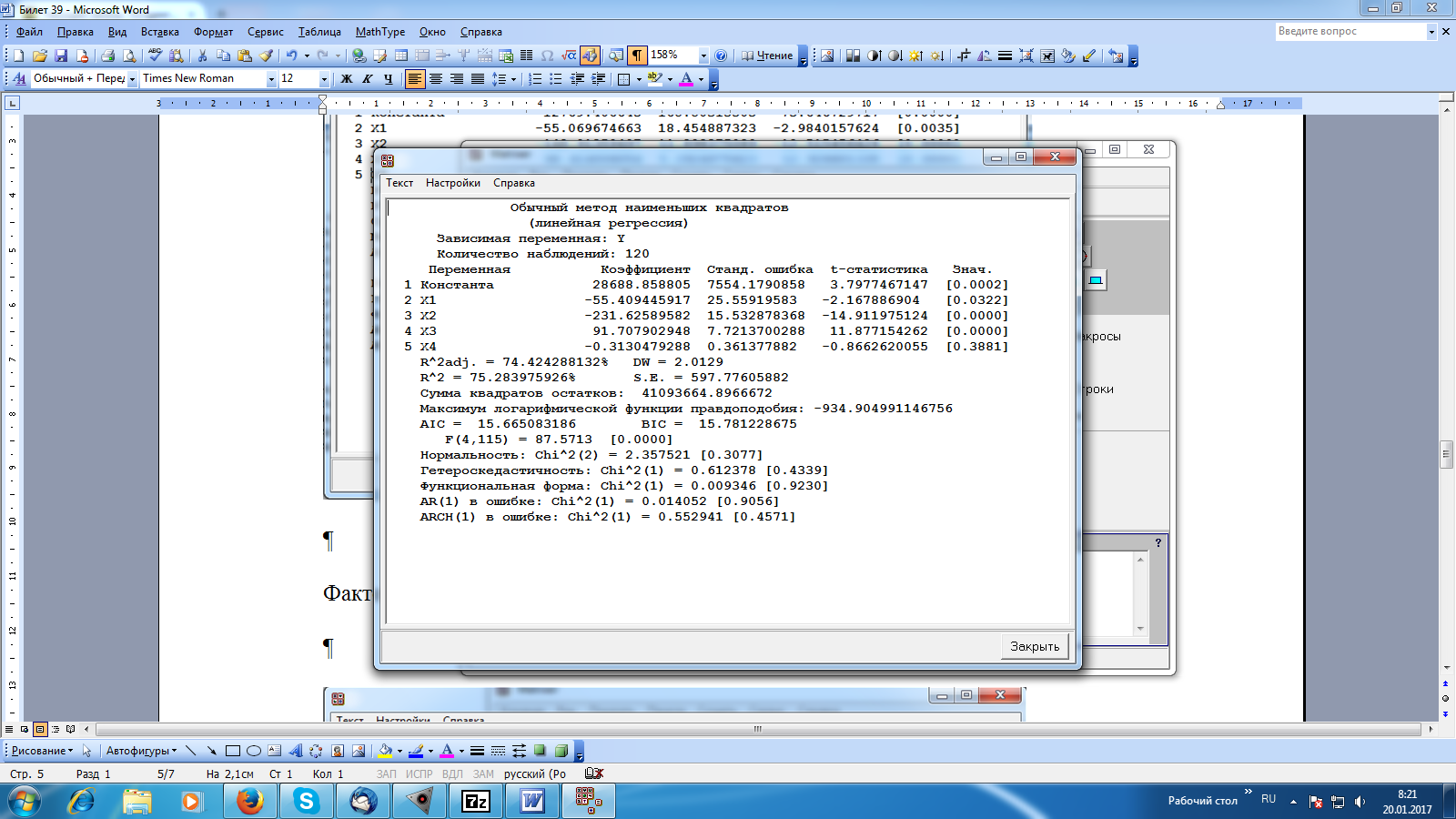 Фактор X4 все равно незначимый, поэтому исключаем его тоже: 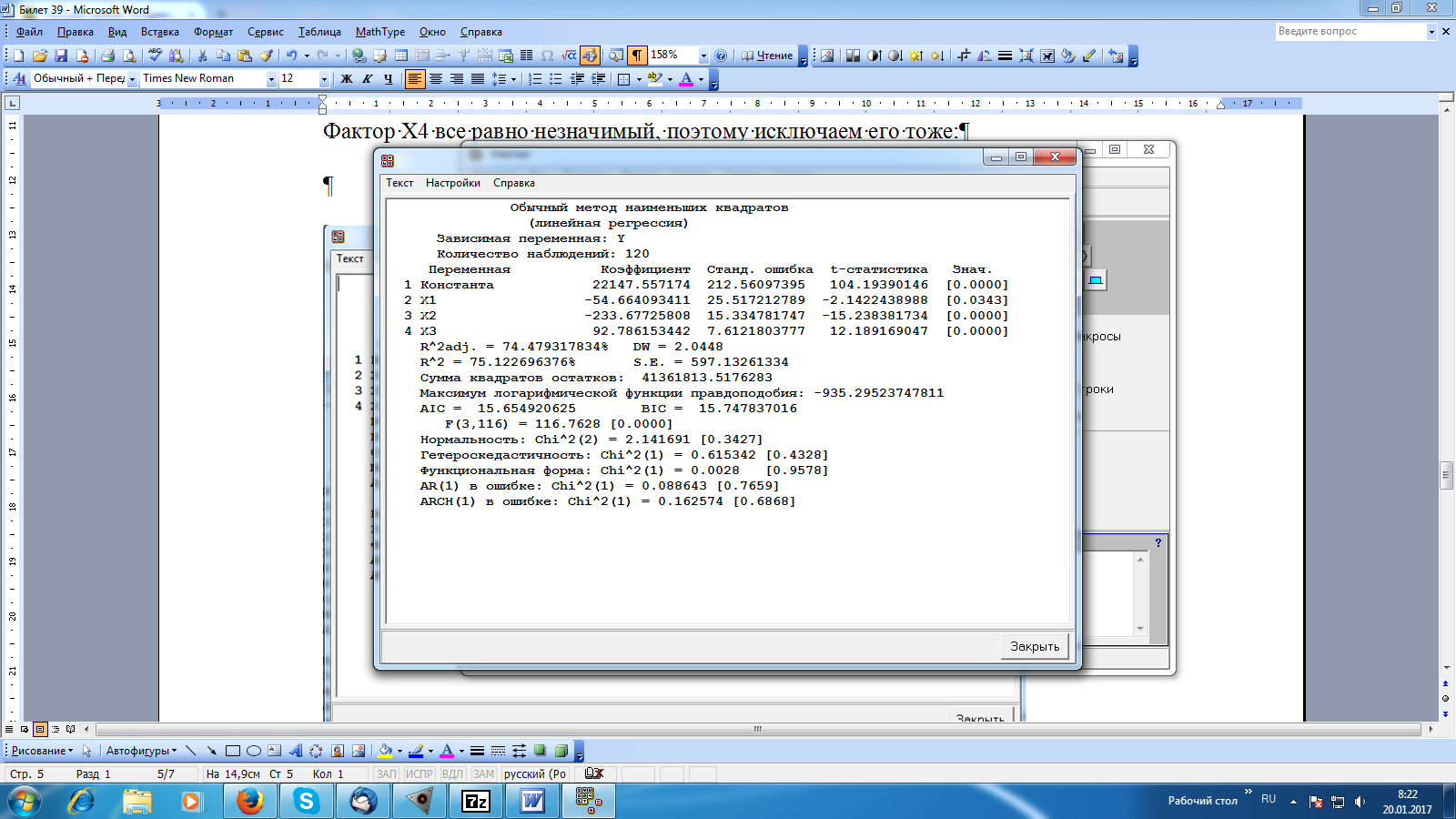 В этом уравнении все коэффициенты значимы, также остатки можно признать нормально распределенными, гетероскедастичности нет, а форму можно считать линейной. Новое уравнение (со значимыми факторами): Y=22147,557-55,664X1-233,677X2+92,786X3 Сравнивая значения коэффициентов с коэффициентами в предыдущей модели, делаем вывод, что знаки коэффициентов сохранились, т.е. направление связи осталось прежним, а значения незначительно изменились. По полученному равнению можно сделать следующие выводы: чем больше жителей живет недалеко от магазина (при неизменных значениях остальных факторов), тем выше изучаемая цена на товар (в среднем — приблизительно 92,786 рубля на каждую тысячу человек); чем больше число конкурентов (при неизменных значениях других факторов), тем меньше цена на товар (в среднем на 55,664 руб. на каждого конкурента); чем ближе магазин расположен к метро (при неизменных значениях других факторов), тем выше цена (в среднем на 233,677 руб. на каждые 100 м), соответственно, чем дальше магазин от метро, тем ниже должна быть цена. Проблема эндогенности является очень частой причиной получения неадекватных, ошибочных результатов оценивания взаимосвязей между экономическими величинами. Суть проблемы эндогенности — это корреляция переменной и ошибки в уравнении регрессии. В данном случае источниками такой проблемы может быть, например, тот факт, что причинно-следственная связь между зависимой переменной и той, которая подозревается на эндогенность, двунаправленна: если цена конкурентов влияет на цену в данном магазине, то и этот магазин является чьим-то конкурентом, а значит, и сама цена в нем влияет на цену его конкурентов; корреляция переменной «цена у конкурентов» и ошибки в уравнении неизбежна. Другой пример возможной эндогенности в этой задаче — это ошибка измерения факторов. В описании многих переменных значится «экспертная оценка», что напрямую свидетельствует об ошибках измерения, характер которых установить вряд ли представляется возможным. Если эти ошибки связаны с зависимой переменной, то снова неизбежна корреляция фактора, измеренного с ошибкой, и ошибки в уравнении регрессии. Оценки параметров уравнений регрессии с эндогенными факторами являются смещенными, и часто характер смещения сложно определить. Таким образом, получив незначимую оценку влияния переменной «цена конкурентов» мы не можем гарантировать, что этого влияния нет, если подозреваем эндогенность этой переменной. То же самое касается и полученных значимых результатов; в случае эндогенности фактора смещение оценки коэффициента при нём в уравнении регрессии может изменить даже знак коэффициента. В нашем итоговом уравнении осталось только 3 фактора — количество «конкурирующих» магазинов рядом , количество людей, проживающих рядом с магазином, и расстояние от магазина до метро. Хотя эти переменные носят статус «экспертных оценок», вряд ли разумно подозревать их эндогенность — даже если они измерены с ошибками, эти ошибки, скорее всего, не связаны с зависимой переменной; сами же переменные являются пространственными характеристиками расположения магазина и маловероятно, что на них может повлиять цены на товар в магазине. Однако, если мы хотим получить более надежную картину оценки влияния цен конкурентов (и, возможно, других факторов, которые были исключены), то необходимо учесть проблему эндогенности. Решение проблемы эндогенности, как правило, сводится к поиску инструментальных переменных. Если есть переменные, которые для некоторого эндогенного фактора являются годными и сильными инструментами, то они помогут устранить корреляцию данного фактора с ошибкой уравнения регрессии. Зачастую поиск адекватных инструментов — задача, гораздо более сложная и трудоемкая, чем все остальное исследование. Например, в нашей задаче мы ограничены имеющимися данными и фактически не можем получить дополнительную информацию. Если бы мы находились в ситуации реального исследования, то необходимость решить проблему эндогенности, скорее всего, привела бы к необходимости дополнительных данных, а именно — поиска годных и сильных инструментов. В случае нашей переменной «цена конкурентов» годным и сильным инструментом будет переменная, которая связана с ценой конкурентов, но не связана с ошибкой в уравнении. К сожалению, любая переменная, связанная с политикой ценообразования и маркетингом (акции, скидки и т.п.) будет иметь ту же проблему, что и цена конкурентов — взаимовлияние «данного магазина» и «конкурентов». Остается искать только среди некоторых пространственных характеристик магазинов, которые влияют на цену конкурентов, но не связаны с ошибкой в оценке цены данного магазина. По примеру итогового построенного уравнения подошла бы оценка расстояния от конкурирующих магазинов до метро, а также количество проживающих рядом с конкурирующими магазинами людей; этих данных, конечно, мы не имеем, однако, обратим внимание, что конкуренты в переменной «цена конкурентов» рассматриваются только ближайшие, т.е. эти переменные вполне могут послужить и инструментами для них. |
