Вариант 3
Задание 2
Задача 1
Два тела массами 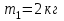 и и 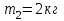 с вязаны невесомой нитью перекинутой через невесомый блок (Рис. 1). Наклонные плоскости по которым скользят грузы, составляют с горизонтом углы с вязаны невесомой нитью перекинутой через невесомый блок (Рис. 1). Наклонные плоскости по которым скользят грузы, составляют с горизонтом углы 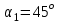 и и 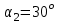 соответственно, а коэффициенты трения между грузами и плоскостями равны соответственно, а коэффициенты трения между грузами и плоскостями равны 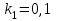 и и 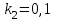 соответственно. Трением в блоке можно пренебречь. В какую сторону движутся грузы влево или вправо? Найти ускорение aгрузов и силу натяжения Т нити. Ускорение свободного падения соответственно. Трением в блоке можно пренебречь. В какую сторону движутся грузы влево или вправо? Найти ускорение aгрузов и силу натяжения Т нити. Ускорение свободного падения 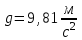 . .
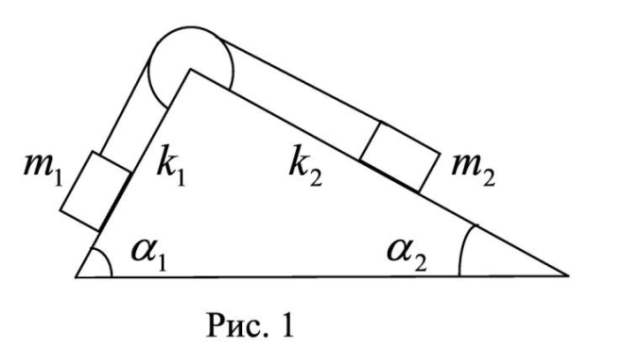
Рис. 1.
Дано:
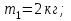
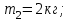
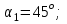
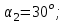
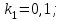
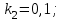
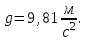
|
Решение:
Рассмотрим рисунок 1 на котором обозначим все силы действующие на тела и зададим систему отсчёта.
Возможны 4 варианта.
1) Грузы движутся влево;
2) Грузы движутся вправо;
3) Грузы стоят.
4) Грузы движутся с постоянной скоростью.
Предположим, что грузы движутся влево. Обозначим ускорение тел.
Запишем уравнение второго закона Ньютона для каждого из тел.
Для первого тела:
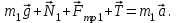
Для второго тела:
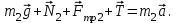
|
Найти:
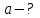
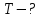
|
Спроектируем векторы сил и ускорения на оси координат:
Для первого тела:
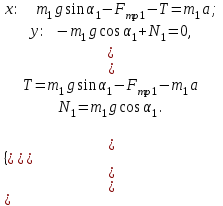
Учитывая, что 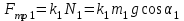 , получаем: , получаем:
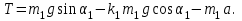
Для второго тела:
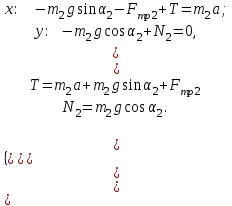
Учитывая, что 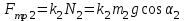 , получаем: , получаем:
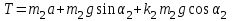
Приравнивая силу натяжения нити для первого и второго тела, вычисляем ускорение:
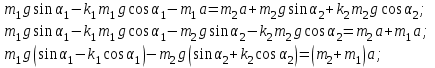
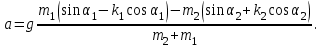
Подставим численные значения и вычислим. Если получим отрицательное ускорение, следовательно, наше предположение не верно и тела стоят или движутся влево с постоянной скоростью.
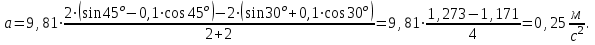
Следовательно, грузы движутся влево.
Вычисляем силу натяжения нити используя формулу:
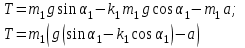
Подставим численные значения и вычислим.
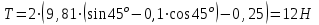 . .
Ответ: Грузы движутся влево; 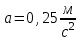 ; ; 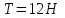 . .
|
Задача 2
Средняя плотность планеты 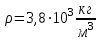 , её радиус , её радиус 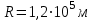 , период обращения планеты вокруг своей оси - , период обращения планеты вокруг своей оси - 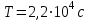 . Найти вес тела массой . Найти вес тела массой 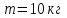 на экваторе планеты. на экваторе планеты.
Дано:
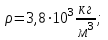
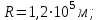
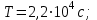
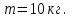
|
Решение:
Рассмотрим рисунок 2.
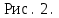
Запишем второй закон Ньютона, учитывая, что сила тяжести предаёт телу центростремительного ускорения.
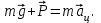
Спроектируем векторы сил и ускорения на ось х.
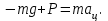
Где 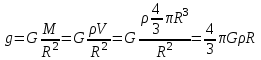 - ускорение свободного падения на планете, - ускорение свободного падения на планете, 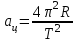 - центростремительное ускорение, - центростремительное ускорение, 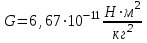 - гравитационная постоянная. - гравитационная постоянная.
После подстановки, получаем:
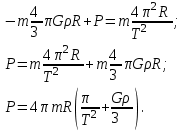
Подставим значения и вычислим:
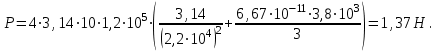
Ответ: 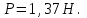
|
Найти:
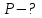
|
Задача 3
На однородный цилиндрический блок массой 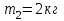 и радиусом и радиусом 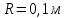 намотана невесомая нить, к свободному концу которой прикреплён груз массой намотана невесомая нить, к свободному концу которой прикреплён груз массой 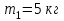 . К блоку крестообразно прикреплены четыре одинаковых невесомых стержня на которых закреплены одинаковые грузы массой . К блоку крестообразно прикреплены четыре одинаковых невесомых стержня на которых закреплены одинаковые грузы массой 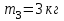 на расстоянии х от оси вращения (Рис. 3). Грузы на расстоянии х от оси вращения (Рис. 3). Грузы 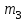 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения а груза можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения а груза 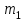 от расстояния х. Построить график этой зависимости в интервале изменения х от R до 3R. Ускорение свободного падения от расстояния х. Построить график этой зависимости в интервале изменения х от R до 3R. Ускорение свободного падения 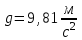 . .
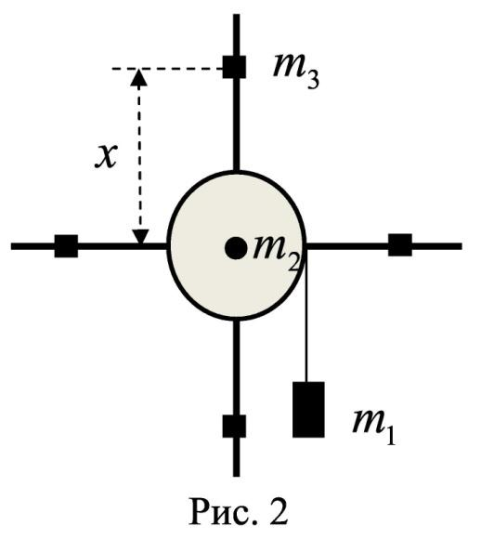
Рис. 3.
Дано:
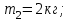
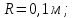
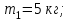
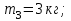
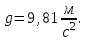
|
Решение:
Зададим систему отсчёта. За начало отсчёта принимаем поверхность земли, ось х направим вертикально вниз. По закону сохранения полной механической энергии, уменьшение потенциальной энергии груза 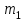 идёт на увеличения кинетической энергии груза идёт на увеличения кинетической энергии груза 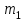 , вращательной кинетической энергии блока и грузов закреплённых на стержнях, поэтому можно записать: , вращательной кинетической энергии блока и грузов закреплённых на стержнях, поэтому можно записать:
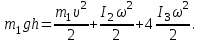
Где 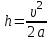 - расстояние, которое проходит груз - расстояние, которое проходит груз 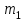 , , 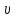 - его скорость, - его скорость, 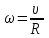 - угловая скорость блока, - угловая скорость блока, 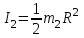 - момент инерции блока относительно оси вращения, - момент инерции блока относительно оси вращения,
|
Найти:
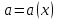
|
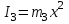 - момент инерции груза закреплённого на стержне относительно оси вращения. - момент инерции груза закреплённого на стержне относительно оси вращения.
После подстановки, получаем:
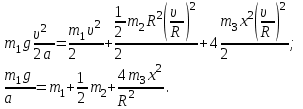
Подставим численные значения физических величин и найдём зависимость ускорения а груза 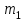 от расстояния х от расстояния х 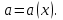
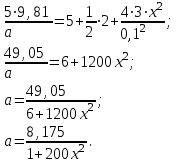
Строим график зависимости 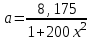 в интервале изменения х от R до 3R рисунок 4. в интервале изменения х от R до 3R рисунок 4.
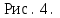
Ответ: 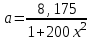
| |
 Скачать 249.1 Kb.
Скачать 249.1 Kb.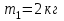 и
и 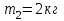 с вязаны невесомой нитью перекинутой через невесомый блок (Рис. 1). Наклонные плоскости по которым скользят грузы, составляют с горизонтом углы
с вязаны невесомой нитью перекинутой через невесомый блок (Рис. 1). Наклонные плоскости по которым скользят грузы, составляют с горизонтом углы 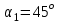 и
и 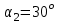 соответственно, а коэффициенты трения между грузами и плоскостями равны
соответственно, а коэффициенты трения между грузами и плоскостями равны 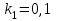 и
и 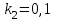 соответственно. Трением в блоке можно пренебречь. В какую сторону движутся грузы влево или вправо? Найти ускорение aгрузов и силу натяжения Т нити. Ускорение свободного падения
соответственно. Трением в блоке можно пренебречь. В какую сторону движутся грузы влево или вправо? Найти ускорение aгрузов и силу натяжения Т нити. Ускорение свободного падения 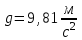 .
.
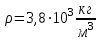 , её радиус
, её радиус 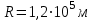 , период обращения планеты вокруг своей оси -
, период обращения планеты вокруг своей оси - 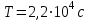 . Найти вес тела массой
. Найти вес тела массой 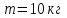 на экваторе планеты.
на экваторе планеты.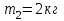 и радиусом
и радиусом 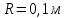 намотана невесомая нить, к свободному концу которой прикреплён груз массой
намотана невесомая нить, к свободному концу которой прикреплён груз массой 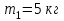 . К блоку крестообразно прикреплены четыре одинаковых невесомых стержня на которых закреплены одинаковые грузы массой
. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня на которых закреплены одинаковые грузы массой 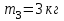 на расстоянии х от оси вращения (Рис. 3). Грузы
на расстоянии х от оси вращения (Рис. 3). Грузы 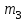 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения а груза
можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения а груза 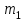 от расстояния х. Построить график этой зависимости в интервале изменения х от R до 3R. Ускорение свободного падения
от расстояния х. Построить график этой зависимости в интервале изменения х от R до 3R. Ускорение свободного падения 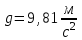 .
.

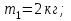
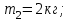
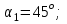
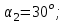
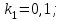
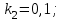
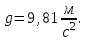
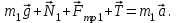
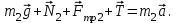
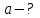
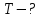
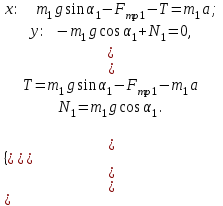
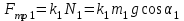 , получаем:
, получаем: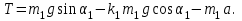
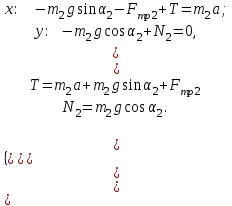
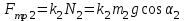 , получаем:
, получаем: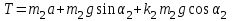
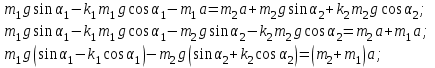
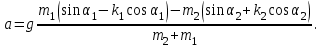
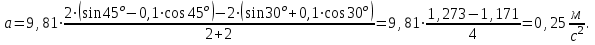
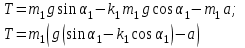
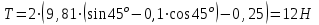 .
.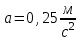 ;
; 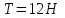 .
.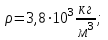
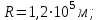
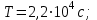
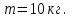
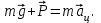
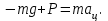
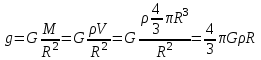 - ускорение свободного падения на планете,
- ускорение свободного падения на планете, 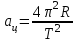 - центростремительное ускорение,
- центростремительное ускорение, 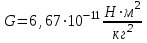 - гравитационная постоянная.
- гравитационная постоянная.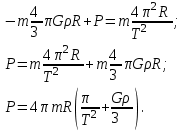
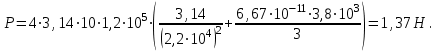
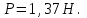
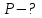
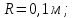
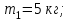
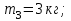
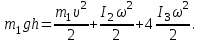
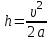 - расстояние, которое проходит груз
- расстояние, которое проходит груз 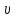 - его скорость,
- его скорость, 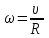 -
- 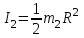 - момент инерции блока относительно оси вращения,
- момент инерции блока относительно оси вращения, 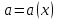
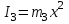 - момент инерции груза закреплённого на стержне относительно оси вращения.
- момент инерции груза закреплённого на стержне относительно оси вращения.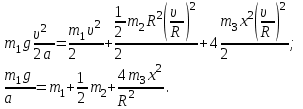
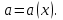
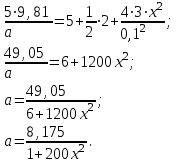
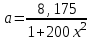 в интервале изменения х от R до 3R рисунок 4.
в интервале изменения х от R до 3R рисунок 4.