Лабораторная работа по ТВиМС. Гратинский_Сергей_УБСТ2102. Решение Рассмотрим все соединения цепи. Элементы 23 и 45 соединены последовательно, (23) и (45) параллельно, 1 с оставшимися элементами последовательно
 Скачать 344.08 Kb. Скачать 344.08 Kb.
|
|
Электрическая цепь состоит из пяти элементов, безотказная работа которых в заданный промежуток времени – независимые события, имеющие веростности  каждый. Найти вероятность Q безотказной работы цепи за данный промежуток времени. каждый. Найти вероятность Q безотказной работы цепи за данный промежуток времени. Решение: Рассмотрим все соединения цепи. Элементы 2-3 и 4-5 соединены последовательно, (2-3) и (4-5) параллельно, 1 с оставшимися элементами последовательно. Вероятность работы цепи с i элементами при последовательном соединении будет равна  Вероятность работы цепи с i элементами при параллельном соединении будет равна  , ,  Решаем задачу поэтапно. Рассмотрим элементы 2-3, вероятность их работы вычисляется как: 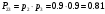 Элементы 4-5 соединены также последовательно, тогда: 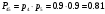 Группа элементов (2-3) и (4-5) соединены параллельно, вероятность работы данного участка:  Элемент 1 соединён с остальной цепью последовательно, тогда вероятность работы цепи в целом:  Ответ:  2. Дискретная случайная величина задана законом распределения  . Найти величину . Найти величину  , построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. , построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
Решение:  Функция распределения СВ: 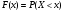 Если 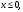 тогда тогда  Если  тогда тогда  Если 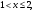 тогда тогда  Если  тогда тогда 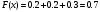 Если  тогда тогда 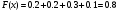 Если  тогда тогда 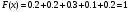 График функции распределения СВ:  Математическое ожидание СВ:  Дисперсия СВ:  Среднее квадрат. отклонение СВ: 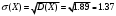 Ответ:  3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:  Найти величину коэффициента  , написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы , написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы  и и 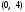 . .Решение: Найдём величину  непрерывной СВ: непрерывной СВ:  Функция распределения непрерывной СВ:  График функции распределения F(x)  Математическое ожидание непрерывной СВ:  Дисперсия непрерывной СВ:  Среднее квадратическое отклонение непрерывной СВ:  Вероятность того, что величина 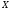 примет значения из заданного интервала примет значения из заданного интервала  : :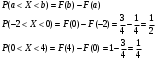 Ответ: 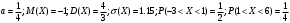 4. Вероятность попадания нормально распределенной случайной величины с математическим ожиданием  в интервал (3; 5) равна 0,6. Найти дисперсию данной случайной величины. в интервал (3; 5) равна 0,6. Найти дисперсию данной случайной величины.Решение: Вероятность того, что нормально распределенная случайная величина примет значение в интервале  определяется формулой: определяется формулой: Здесь Ф(x) – функция Лапласа, которая принимает значения из таблицы  Выше мы воспользовались нечётностью функции Лапласа Ф(-х)=-Ф(х)  Из таблицы определим при каком аргументе функция Лапласа принимает значения 0.3  Ответ:  5. Дискретная случайная величина задана выборкой: 0,-1,0,1,1,-1,-1,0,0,0,-1,0,1,1,0,-1,0,0,0,1,1,1,-1,1,1 Построить полигон частот и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию. Решение: Число элементов в выборке  Воспользуемся вспомогательной таблицей
Здесь 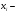 значения из выборки, значения из выборки, 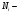 частоты элементов выборки, частоты элементов выборки, 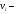 относительная частота равная относительная частота равная 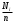 Изобразим полигон частот на графике ниже:  Вычислим эмпирическую функцию распределения 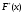 Если 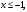  Если  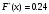 Если  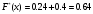 Если  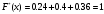 График эмпирической функции распределения:  Выборочное среднее: 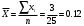 Выборочная дисперсия:  Ответ:  |