Физика. Физика2 (1). Решение Растояние S, которое проехал автомобиль, равно Где u 0 начальная скорость автомобиля

• Название: Решение Растояние S, которое проехал автомобиль, равно Где u 0 начальная скорость автомобиля
• Анкор: Физика
• Дата: 06.04.2023
• Размер: 67.26 Kb.
• Имя файла: Физика2 (1).docx
• Тип: Решение; #1041243

Задача №1

Автомобиль начал двигаться равноускорено по закругленному участку пути и, пройдя расстояние 100 м, развил скорость 21,6 км/ч. Определите тангенциальное, нормальное и полное ускорения автомобиля через 10 с после начала движения. Радиус закругления равен 200 м.

Дано

S=100 м.

U=21,6 км/ч =10 м/с.

R=200 м.

Найти

a _n- ?, a _τ - ?, a -?

Решение



Растояние S, которое проехал автомобиль, равно:



Где U₀ - начальная скорость автомобиля.

t – время движения.

a _τ – тангенциальное ускорения.

Учитывая что начальная скорость равна нулю U₀=0

Выражение имеет вид



Отсюда тангенциальное ускорение автомобиля: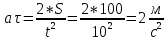



Нормальное ускорение найдем из формулы





Полное ускорение



Ответ: a τ=2 м/с2; а n=2,3 м/с2; а =2,3 м/с2.
Задача №2
Камень массой 1,5 кг упал с некоторой высоты. Падение продолжалось 1,2 с. Определите кинетическую энергию камня в средней точке пути.

Дано

m=1,5 кг

t=1,2c

Найти

E=?



Определяем высоту падения камня в средней точке пути, зная время падения, найдем высоту падения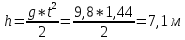



Определяем. Потенциальная энергия на половинной высоте


Потенциальная энергия на половинной высоте равна половине полной энергии. Т.к. для системы выполняется закон сохранения механической энергии, то

По закону сохранения энергии Е(п) =Е (к)

Ответ: Е(п) =Е (к) 51,86 Дж

Задача №3

Шар массой 4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость оси шара 1м/с . Определить полную кинетическую энергию шара.

Дано

m=4 кг

V=1 м/c

Найти

Eк=?

Решение

Кинетическая энергия шара складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения .

; I для шара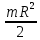

где m -масса шара

R-радиус шара

Отсюда

Е_к=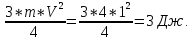

Ответ Е_к=3 Дж.


Задача №4

В баллоне вместимостью 2 л находится одноатомный газ под давлением 780 мм рт. ст. Определите среднюю кинетическую энергию движения всех молекул газа.

Дано

Р=780 мм рт. ст. (1*10⁵ Па)

V=2 л (2*10^-3 м³)

Найти

Eк=?

Решение

По закону о равномерном распределении энергии по степеням свободы молекул, на каждую степень свободы молекулы газа приходится в среднем энергия, равная: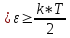



где к - постоянная Больцмана;

Т - температура газа.

Молекула любого газа имеет 3 поступательные степени свободы, поэтом, средняя кинетическая энергия поступательного движения молекулы газа:



Выразим концентрацию и молекул газа через давление р и температуру Т газа:



Концентрация п - число молекул в единице объёма. Тогда в объёме V содержится число молекул:



Следовательно, кинетическая энергия поступательного движения всех молекул, находящихся в данном объёме, равна:




Задача №5

В вершинах квадрата со стороной 10 см находятся заряды по 2 нКл (рисунок). Определите в центре квадрата: 1) напряженность поля; 2) потенциал поля.

Д 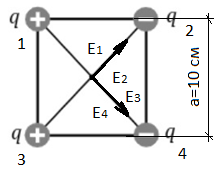ано

q 1, q 3 = 2^-10 Кл;

q 2 ,q 4 = -2^-10 Кл;

а = 0,1 м.

Найти

, φ

Решение

Напряженность   поля, создаваемого системой зарядов, равна геометрической сумме напряженностей   полей, создаваемых каждым из зарядов:

Е = Е ₁ + Е ₄,

а так как Е ₁ = Е ₄, то Е = 2 Е ₁ или ,



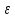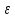где - диэлектрическая проницаемость (для воздуха = 1),

   – расстояние от центра квадрата до заряда.



Потенциал j поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов j полей, создаваемых каждым из зарядов:

j = j₁ + j₂ + j₃ + j₄.

Учитывая знаки зарядов, имеем j = j₁+ j₃, а так как j₃ = j₁, то j = 2j₃.

Задача №9

Из проволоки длиной 3,14 м и сопротивлением 2 Ом сделано кольцо. Определите индукцию магнитного поля в центре кольца, если на концах провода создана разность потенциалов 1 В.

Дано

L=3,14 м.

R=2 Ом.

=1В

Найти

В-?

Решение

индукция магнитного поля  в центре кругового витка с током:

B=μ⋅μ0⋅I2R,
μ  – относительная магнитная проницаемость среды (нет специальных оговорок, считаем μ = 1),

μ0 = 4π∙10^–7 Гн/м – магнитная постоянная,

 R – радиус кольца, 

I – сила тока в кольце. Силу тока найдём по закону Ома:

I=Ur.
Радиус кольца определим, зная длину проволоки (длина окружности):

L = 2π∙R,  R = L / 2π.

I, R подставляем в формулу индукции и получаем ответ:

B=μ0⋅U⋅πr⋅L.


Ответ: 6,28∙10^-7 Тл.