задачи по физике. Вариант 5. Решение Разобьем проводящее кольцо на элементарные отрезки. Магнитная индукция поля, создаваемого этим элементом в точке а определяется по закону БиоСавараЛапласа, где магнитная постоянная, радиусвектор, проведенный от элемента проводника в точку А
 Скачать 210.38 Kb. Скачать 210.38 Kb.
|
|
Вариант 5 405.По тонкому кольцу радиусом 20 см течет ток 100А. Определить магнитную индукцию В на оси кольца в точке А (рис18). Угол β=π/3.
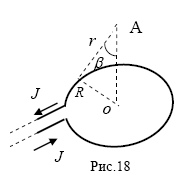 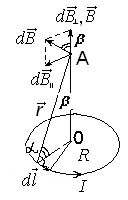 Разобьем проводящее кольцо на элементарные отрезки 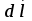 . Магнитная индукция поля . Магнитная индукция поля  , создаваемого этим элементом в точке А определяется по закону Био-Савара-Лапласа: , создаваемого этим элементом в точке А определяется по закону Био-Савара-Лапласа: 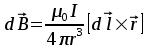 , где , где 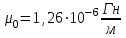 – магнитная постоянная, – магнитная постоянная, 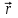 - радиус-вектор, проведенный от элемента проводника - радиус-вектор, проведенный от элемента проводника 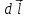 в точку А. в точку А.По правилу буравчика определим направление  . По принципу суперпозиции магнитная индукция . По принципу суперпозиции магнитная индукция 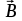 равна сумме магнитных индукций равна сумме магнитных индукций  от всех элементарных отрезков от всех элементарных отрезков 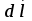 проводника проводника 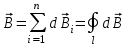 (интегрирование ведется по длине проводящего кольца). Разложим вектор (интегрирование ведется по длине проводящего кольца). Разложим вектор  на две составляющие: на две составляющие: 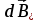 - перпендикулярную плоскости кольца и - перпендикулярную плоскости кольца и 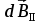 - параллельную плоскости кольца, то есть - параллельную плоскости кольца, то есть 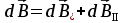 . .Тогда 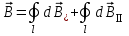 . Заметим, что . Заметим, что 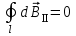 из соображений симметрии и что векторы из соображений симметрии и что векторы 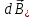 от различных элементов от различных элементов 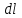 сонаправлены, поэтому можно заметить векторное интегрирование скалярным: сонаправлены, поэтому можно заметить векторное интегрирование скалярным: 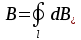 , где , где 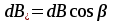 , где , где 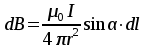 , где α – угол между элементом , где α – угол между элементом 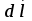 и радиус-вектором и радиус-вектором 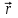 , проведенным от элемента в точку А. , проведенным от элемента в точку А.Из рисунка видно, что 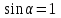 , так как , так как 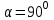 , , 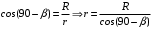 , , где R – радиус кольца, 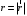 равноудаленной от всех точек кольца. равноудаленной от всех точек кольца. С учетом этого получаем 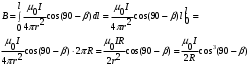 . .Подставим числовые значения, получим: 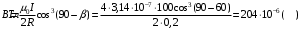 Ответ: В=204 мкТл. 415.По тонкому проводу, согнутому в виде прямоугольника, течет ток силой 60А. Длина сторон прямоугольника равна 30 и 40 см. Определить магнитную индукцию В в точке пересечения диагоналей.
По принципу суперпозиции магнитных полей магнитная индукция 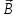 будет равна геометрической будет равна геометрическойсумме магнитных индукций полей, создаваемых каждой стороной прямоугольника АЕСD. 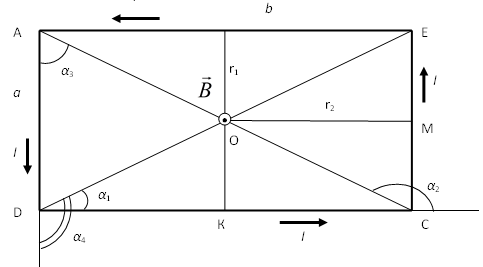 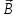 = =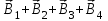 . .В точке О все 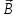 направлены одинаково (к нам), перпендикулярно плоскости витка. направлены одинаково (к нам), перпендикулярно плоскости витка.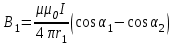 ; ;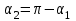 ; ; 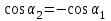 . .μ = 1, 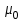 = 4π∙10 -7 Гн/м – магнитная постоянная. = 4π∙10 -7 Гн/м – магнитная постоянная.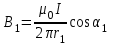 . .r1= а /2, r2= b/2 . Диагонали прямоугольника делятся в точке пересечения пополам, поэтому вычислим cos α1 из соотношения 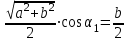 (Δ DОК) (Δ DОК)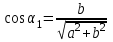 ; ;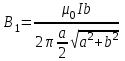  . .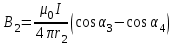 ; ;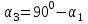 ; ; 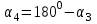 ; ; 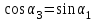 ; ; 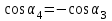 . .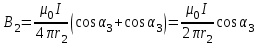 . .Из Δ ЕОМ 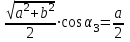 . . 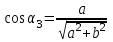 ; ; 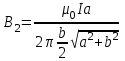 . .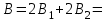 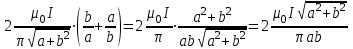 . .Подставим числовые значения, получим: 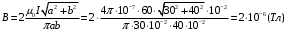 Ответ: В= 2 мкТл. 425.Тонкий провод длиной 20 см согнут в виде полукольца и помещен в магнитное поле (10мТл) так, что площадь полукольца перпендикулярна линиям магнитной индукции. По проводу пропустили ток 50А. Определить силу, действующую на провод. Подводящие провода направлены вдоль линий магнитной индукции.
 Непосредственно применить закон Ампера в виде 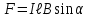 нельзя, т.к. каждый элемент проводника расположен неодинаковым образом относительно магнитного поля. Разделим проводник на столь малые участки, чтобы каждый из них можно было считать элементом тока. Рассмотрим один такой участок, длина которого равна нельзя, т.к. каждый элемент проводника расположен неодинаковым образом относительно магнитного поля. Разделим проводник на столь малые участки, чтобы каждый из них можно было считать элементом тока. Рассмотрим один такой участок, длина которого равна 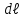 . Модуль вектора элементарной силы, действующей на этот участок, по закону Ампера имеет вид: . Модуль вектора элементарной силы, действующей на этот участок, по закону Ампера имеет вид: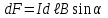 Все элементарные векторы  направлены вдоль оси Оz. Поэтому результирующую силу F можно найти интегрированием, учтя при этом, что направлены вдоль оси Оz. Поэтому результирующую силу F можно найти интегрированием, учтя при этом, что 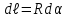 . .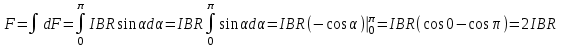 Подставим значения величин, получим: 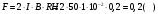 . .Ответ: сила, действующая на проводник равна 0,2 Н. 435. Заряженная частица прошла ускоряющую разность потенциалов 100 В и, влетев в однородное магнитное поле с магнитной индукцией 0,1 Тл, стала двигаться по винтовой линии с шагом 6,5 см и радиусом 1 см. Определите удельный заряд чатицы.
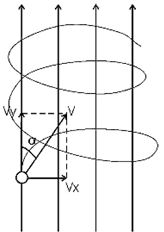 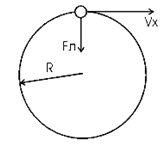 Разложим вектор скорости νчастицы на две составляющие (рис.): v1,направленную вдоль линий магнитной индукции, и v2, перпендикулярную этим линиям. Модули этих составляющих - соответственно υх= νcos α и vу =υ sinα На частицу действует сила Лоренца, обусловленная составляющей vх. 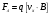 Вследствие этого частица движется по окружности со скоростью vхв плоскости, перпендикулярной магнитному полю. Радиус этой окружности определим, составив уравнение на основании второго закона Ньютона. Вследствие этого частица движется по окружности со скоростью vхв плоскости, перпендикулярной магнитному полю. Радиус этой окружности определим, составив уравнение на основании второго закона Ньютона. 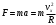 , приравнивая эти две силы выразим скорость электрона вдоль оси ох: , приравнивая эти две силы выразим скорость электрона вдоль оси ох: 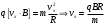 . .За период Т электрон проходит окружность периметром 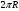 , и поэтому скорость , и поэтому скорость 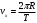 . За это же время электрон проходит вдоль поля расстояние h, поэтому . За это же время электрон проходит вдоль поля расстояние h, поэтому 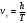 . .Тогда время одного оборота 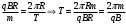 Полная скорость электрона 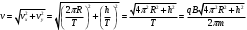 Из закона сохранения энергии получаем, что потенциальная энергия электрона 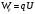 , проходящего через разность потенциалов U, должна быть равна кинетической энергии , проходящего через разность потенциалов U, должна быть равна кинетической энергии 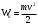 , т.е. , т.е. 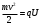 , отсюда выразим искомую величину , отсюда выразим искомую величину 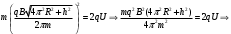 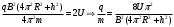 Подставим числовые значения, получим 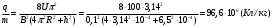 Ответ: q/m=96,6 МКл/кг 445. Квадратный контур со стороной 10 см в котором течет ток силой 6 А находится в магнитном поле с индукцией В = 0,8 Тл под углом φ = 50° к линиям индукции. Какую работу А нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму с квадрата на окружность?
Площадь квадратного контура 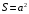 Виток площадью S, по которому течет ток I, обладает магнитным моментом 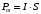 . .Магнитный момент в поле В обладает потенциальной энергией 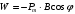 где φ – угол между 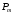 и В. и В.Тогда начальная потенциальная энергия квадратной рамки равна 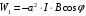 Периметр этой рамки не изменяется при изменении формы и равен 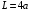 . После того как форму изменили на круг его периметр . После того как форму изменили на круг его периметр 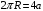 , откуда находим радиус круга , откуда находим радиус круга 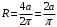 , площадь круга равна , площадь круга равна 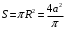 Этот виток обладает потенциальной энергией  Работа равна разности потенциальных энергий 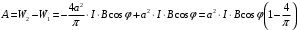 Подставим числа, получим 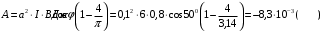 Ответ: А= 8,3 мДж. 445. Рамка из провода сопротивлением 0,04 Ом равномерно вращается в однородном магнитном поле (В = 0,6 Тл ). Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции Площадь рамки S =200 см2. Определить заряд Q, который потечет по рамке при изменении угла между нормалью к рамке и линиями индукции: 1) от 0 до 45°; 2) от 45 д о 90°.
При повороте рамки происходит изменение магнитного потока. В рамке возникает ЭДС индукции 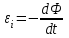 , (1) , (1)приводящая к появлению в рамке индукционного тока. Мгновенное значение этого тока можно определить из закона Ома: 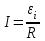 . (2) . (2)Подставив (2) в (1), получим 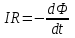 . (3) . (3)Мгновенное значение силы индукционного тока 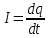 . (4) . (4)Тогда выражение (3) примет вид 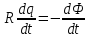 или или 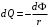 . (5) . (5)Проинтегрировав полученное выражение, найдем 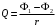 . (6) . (6)По определению магнитного потока = Bscos, где s – площадь рамки. Тогда 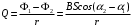 Вычисления: 1) 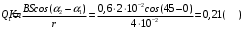 2) 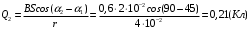 Ответ:Q1=Q2=0.21Кл 465. Соленоид содержит 800 витков. Площадь S сечения сердечника (из немагнитного материала) равна 10см2 . По обмотке течет ток, создающий поле с индукцией 8 мТл. Найти среднее значение ЭДС индукции, возникающей в соленоиде, если ток уменьшается до нуля за время 0,6 мс.
Мгновенное значение ЭДС индукции определяется уравнением Фарадея - Максвелла 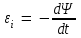 , (1) , (1)где 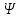 - потокосцепление, связанное с магнитным потоком Ф и числом витков Nсоотношением - потокосцепление, связанное с магнитным потоком Ф и числом витков Nсоотношением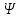 = NФ. (2) = NФ. (2)Подставляя выражение (2) в формулу (1), получаем 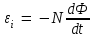 . .Среднее значение эдс за время t определяются выражением: 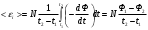 Отсюда, т.к. по условию задачи ток уменьшится до нуля, то Ф2=0 По определению магнитный поток 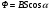 , где α=0. , где α=0.Тогда 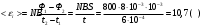 Ответ: <Ԑi> =10,7 В. |
