Решение_3. Решение Рис. 5
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Исходные данные  Рис. 2. Карточка задания 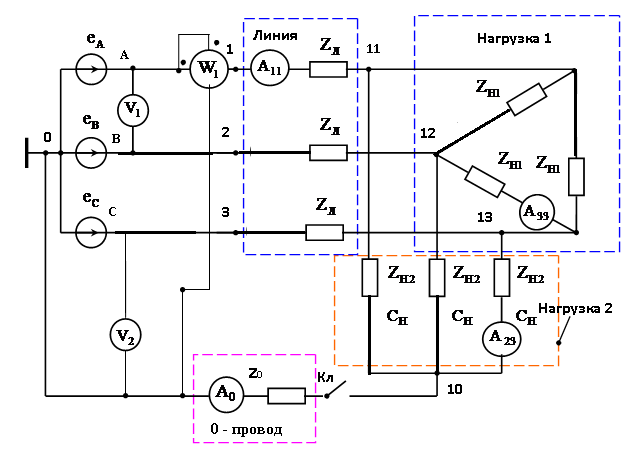 Рис. 3. Расчетная схема, составленная по карточке рис. 2 Дана трехфазная линейная симметричная цепь (рис. 3): - сопротивление линейных проводников Zл= R+jXL-jXC=400+j700-j700=400 Ом; - сопротивление нулевого провода Z0=R - jXC=400-j900 Ом; - реактивное индуктивное сопротивление по первой гармонике первой, соединённой звездой, симметричной нагрузки Zн1= jXL =j1500 Ом - реактивное ёмкостное сопротивление по первой гармонике второй, соединённой треугольником, симметричной нагрузки Zн2= R - jXC = 400-j500 Ом В цепи симметричный трёхфазный источник пилообразного напряжения (рис.3 табл 3.1 МУ). ЭДС фазы A eA(t) представлено на рис. 4: Em = А =40 В; FI = Ψ = 225°; B = 50 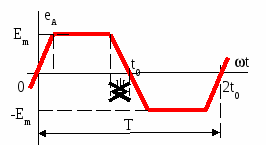 Ψ Рис. 4 Определить для замкнутого и разомкнутого положения ключа: 1. мгновенные значения напряжения uС(t); построить графики uС(t), по 1, 3 и 5 гармоникам. 2. показания вольтметров и амперметров электромагнитной системы и ваттметра электродинамической системы. Решение 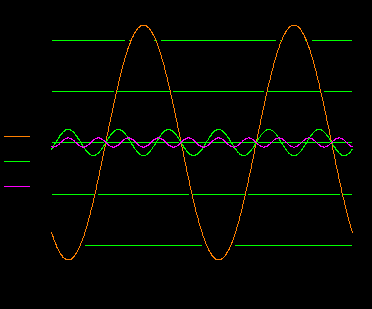 Рис. 5 1. Представим заданное несинусоидальное напряжения eA(t) рис. 4 в виде набора гармоник ряда Фурье . eA(t) = Ограничимся 1, 3 и 5 гармониками. Подставив исходные данные в (11) получим гармонический ряд    eA(t) = -48.853 sin(ωt+B) -5.095 sin(3ωt+3B) +1.783 sin(5ωt+5B). (В). (12) Частота сети f= 50 Гц. Период синусоиды Т = 1/f = 0.02 Частота первой гармоники - = 2π ∕ T =2π ∕ 10–2 = 314 рад/с. Графики составляющих ряда и результирующая кривая показана на рис.5: 2. Расчёт цепи символическим методом по 1, 3 и 5 гармоникам. Для упрощения расчётов преобразуем, сопротивления нагрузки 2, соединённые треугольником, в звезду и получим схему замещения в комплексном виде (рис. 6) для расчётов цепи символическим методом 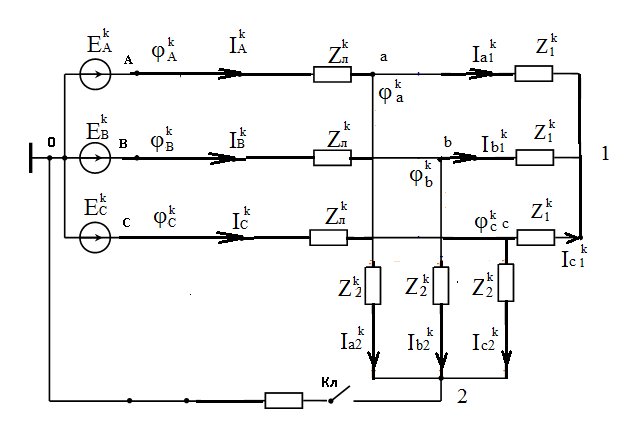 Рис. 6 Реактивные сопротивления для k – й гармоники: X X Сопротивление преобразованной нагрузки Z Z Z Z Z21=400-j500 Z23=400-j500/3=400-j167 Oм Z25=400-j500/5=400-j100 Ом Расчётная схема приведена на рис.6. Особенности расчёта заключаются в том, что гармоники образуют следующие системы ЭДС: первая – симметричная трёхфазная система прямой последовательности фаз: третья – три одинаковых по модулю и фазе ЭДС, система нулевой последовательности фаз: пятая – симметричная трёхфазная система обратной последовательности фаз: 2.1. Расчёт для первой и пятой гармоник k=1,5, для замкнутого и разомкнутого положения ключа 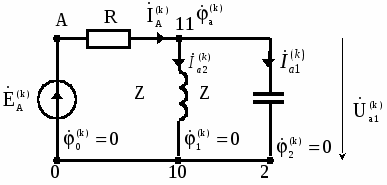 Рис. 7 В связи с тем, что в цепи для первой и пятой гармоники (k = 1,5) ЭДС имеет симметричные трёхфазные системы, а также одинаковые сопротивления в линиях и симметричные нагрузки, применение в расчётах метода узловых потенциалов показывает, что потенциалы узлов «1», «2» и «0» равны нулю ( Расчёт действующих значений токов для гармоник k=1 и 5 (рис. 7) по закону Ома: 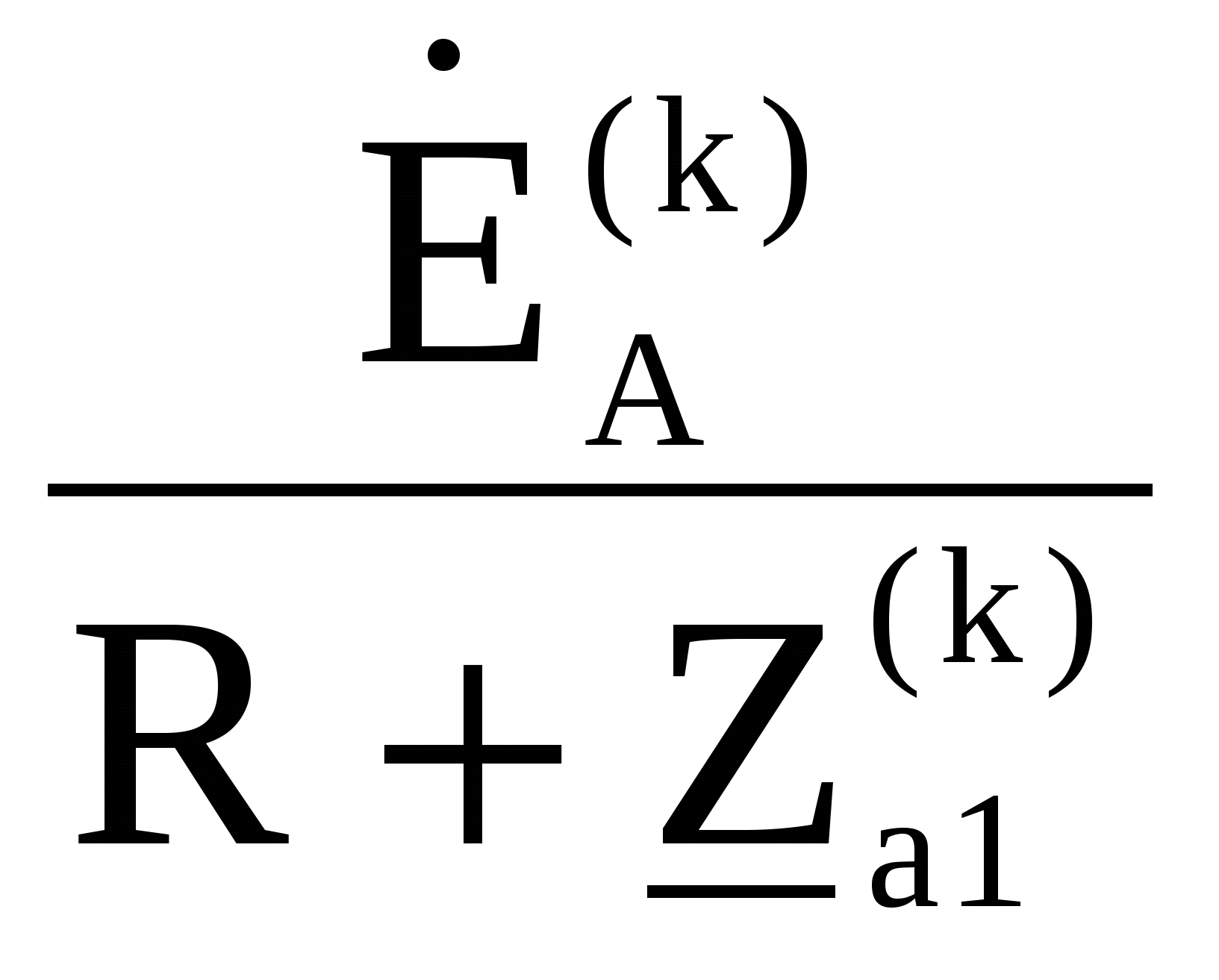 , где Z , где Z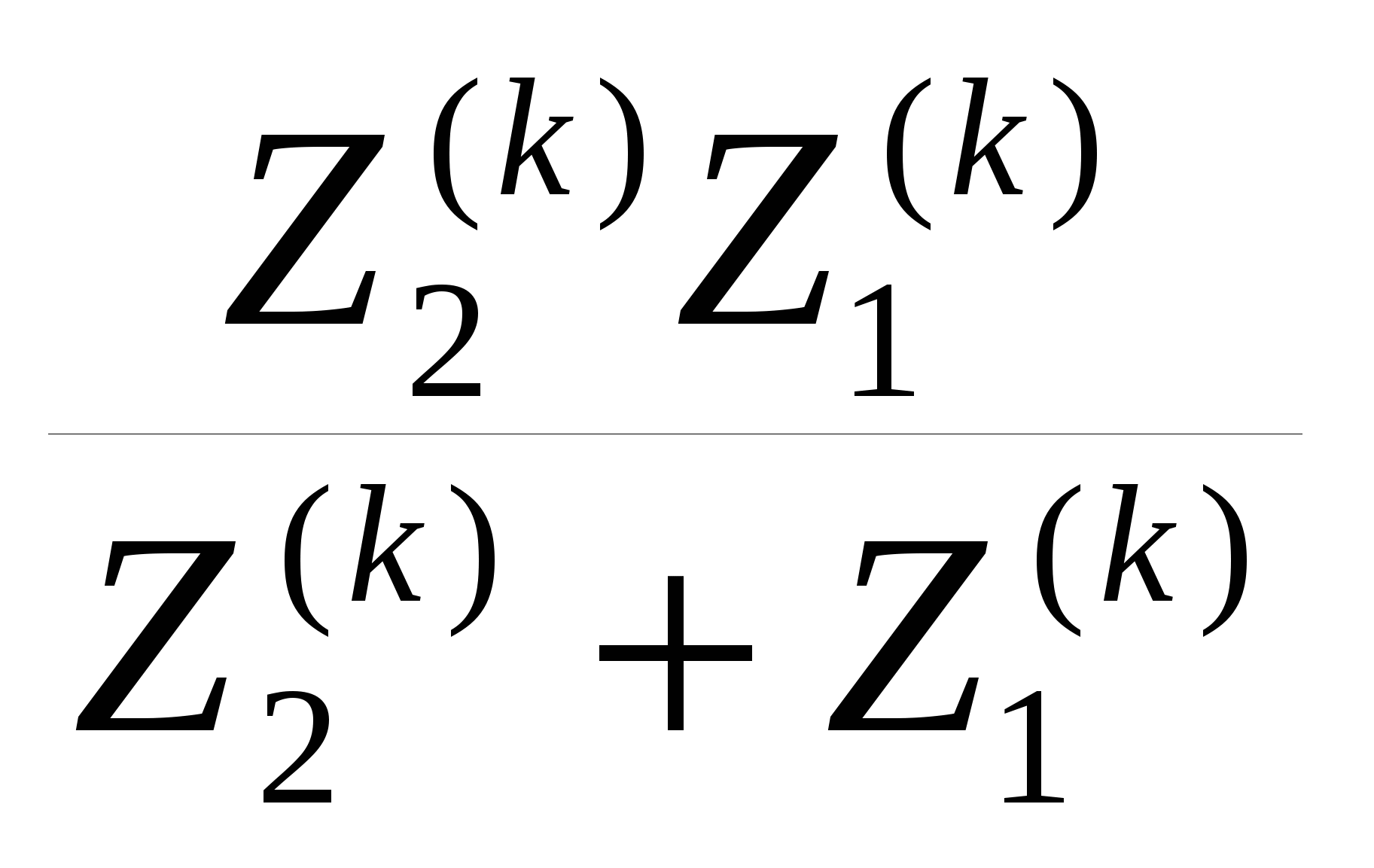 ; ;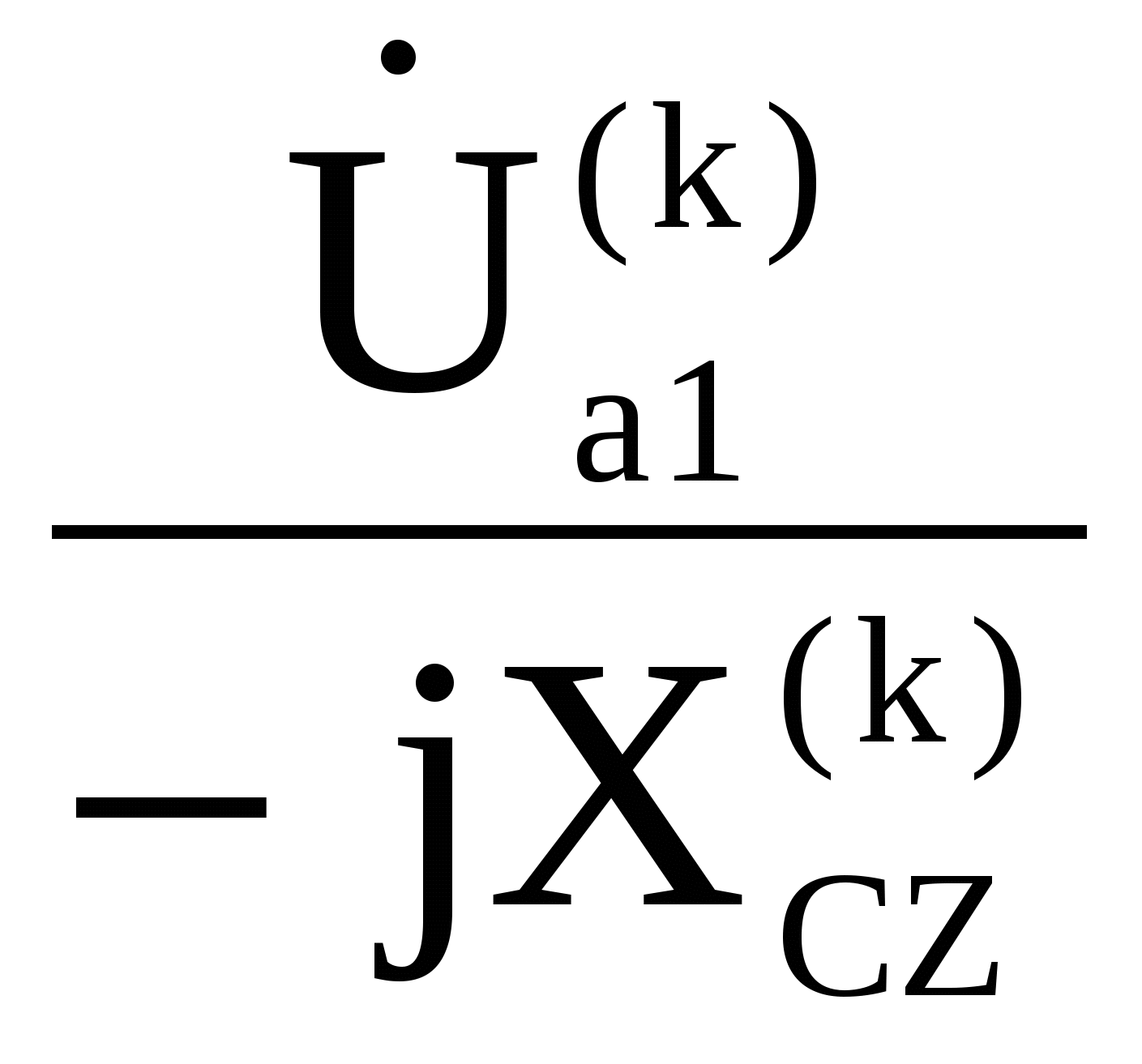 , где , где Первая гармоника k=1. Реактивные сопротивления для первой гармоники. Z Расчёт токов в фазе A. Z Токи в фазе B: Токи в фазе C: Напряжение Ток в первой, не преобразованной нагрузке: Пятая гармоника k=5. Реактивные сопротивления для пятой гармоники. Z Z25=400-j500/5=400-j100 Ом Расчёт токов в фазе A. Z Токи в фазе B: Токи в фазе C: Напряжение Ток во второй, не преобразованной нагрузке: 2.2. Расчёт для третьей гармоник k=3, для замкнутого и разомкнутого положения ключа Реактивные сопротивления для третьей гармоники. Z Z25=400-j500/5=400-j100 Ом Для третьей гармоники в схеме замещения (рис. 6) три одинаковых по модулю и фазе ЭДС, система нулевой последовательности фаз (в курсе лекций l 480 - рис. 1а). Для упрощения расчётов вынесем ЭДС за узел и получим расчётную схему замещения для третьей гармонике рис. 8. 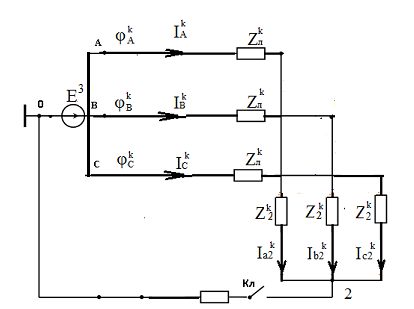 Рис. 8 2.2.1. Расчёт токов для замкнутого положения ключа. Вследствие симметрии нагрузки, потенциалы узлов a, b, c и 2 равны 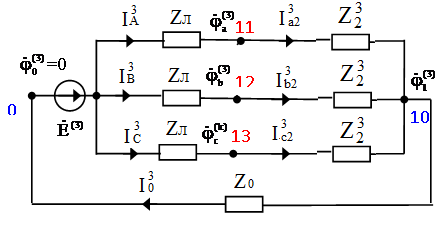 Рис. 9 Ток в нулевом проводе определим по закону Ома: 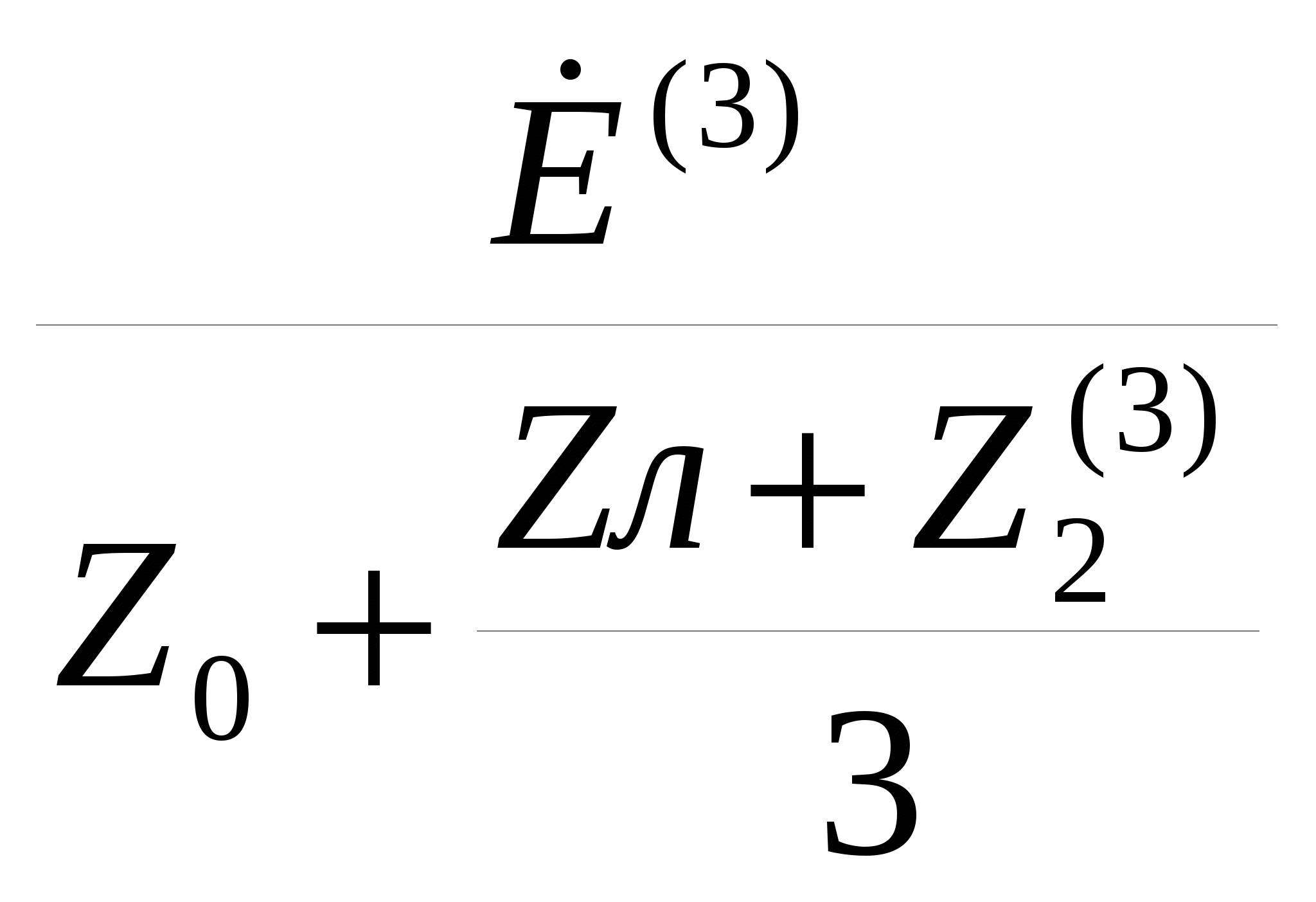 = = 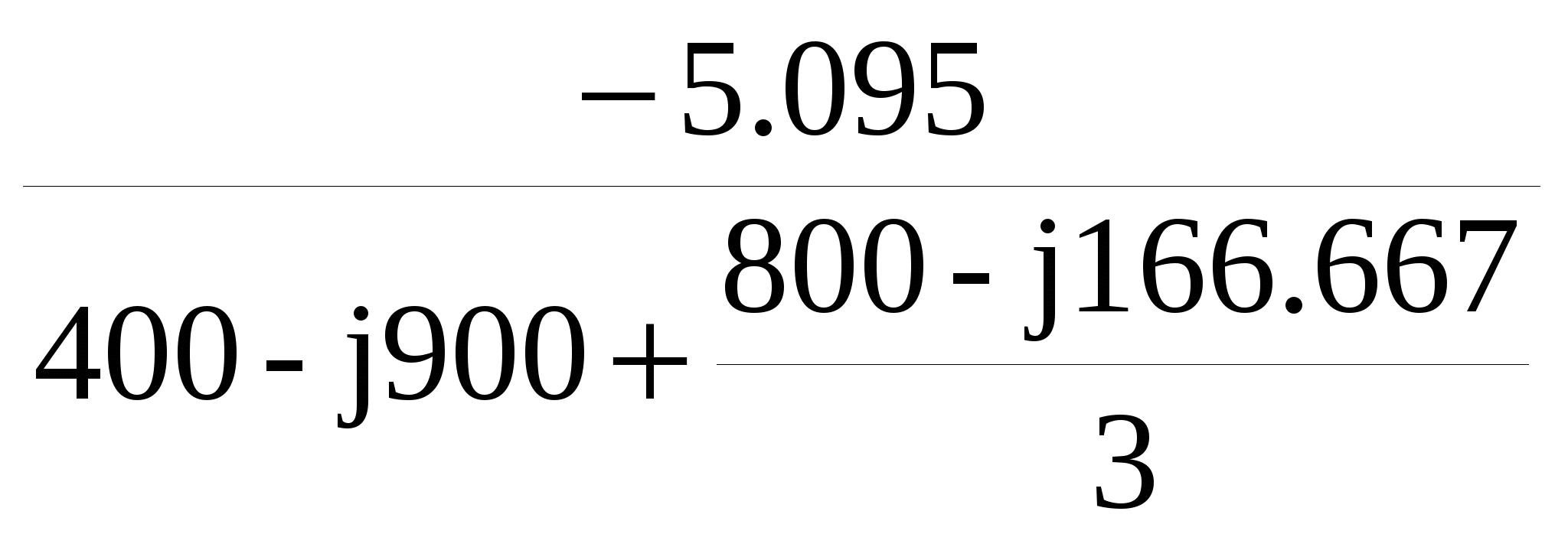 = -2.503*10-3-3.588i*10-3 = = -2.503*10-3-3.588i*10-3 == 0.004∠-124.9° A. Токи в линии и первой нагрузке найдём, как ток в трёх параллельных равных по величине сопротивлениях: Напряжение 2.2.2. Расчёт токов для разомкнутого положения ключа. При разомкнутом ключе и отсутствии нулевого провода потенциалы узлов a, b, c и 2 равны Напряжение
uab(t). = 39.01 sin(ωt-107)+ 0.649 sin[5(ωt+152º)] (В). 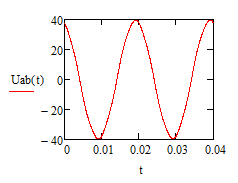 Рис. 10
3.2.1. Вольтметры включены непосредственно на зажимы источника и показывают V1 – линейное напряжение, в котором отсутствуют гармоники кратные 3; V2 – фазное напряжение в котором присутствуют все гармоники. Показания приборов не зависит от положения ключа в нулевом проводе. UV1 = UV2 = 3.2.2. Амперметры показывают действующие значения токов A в линии фазы C, A1 в фазе B первой нагрузки и A2 в ветви a-b второй нагрузки, соединённой треугольником. Показание амперметров A и A1 зависит от положения ключа. При замкнутом ключе присутствуют составляющие всех гармоник IA = IA1 = При разомкнутом ключе в показаниях отсутствуют составляющие гармоник кратных 3. IA = IA1 = Показание амперметров A2 не зависит от положения ключа, так как амперметр находится в ветви a-b второй нагрузки, соединённой треугольником и всегда в показаниях отсутствуют составляющие гармоник кратных 3. IA2 = Показание ваттметра электродинамической системы. Составляющие от 1, 3, и 5 гармоник: PW1 = Re{ PW3 = Re{ PW5 = Re{ Для замкнутого ключа: PW = PW1 + PW3 + PW5 = 0.774 Вт. Для разомкнутого ключа: PW = PW1 + PW5 = 0.77 Вт. Действующее значение напряжения Uab= Таблица 2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
