Решение Рис. Схема механизма подъема груза с кратностью полиспаста К
 Скачать 140 Kb. Скачать 140 Kb.
|
|
Задача № 1 Начертить схему механизма подъема груза с указанной кратностью полиспаста и подобрать канат при заданных в табл.3: грузоподъемности Q, кратности полиспаста Кп и режиме работы. Дано: Q = 5,5 тс, Кп = 4, режим – С, V = 0,2 м/с. Решение    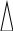   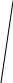 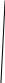    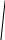             Рис. Схема механизма подъема груза с кратностью полиспаста Кп = 4 По грузоподъемности выбираем одинарный полиспаст (z = 1) с кратностью Kп = 4. Коэффициент полезного действия 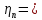 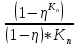 = = 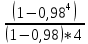 = 0,97. = 0,97.По заданному режиму работы и грузоподъемности выбираем крюковую подвеску 5,0-14А-1-Д630-Д18 массой 120 кг. Определим натяжение ветви каната, набегающей на барабан Smax = 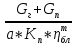 = = 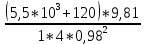 = 14351 Н, = 14351 Н,где m = 2 – число подвижных блоков механизма подъема. Выбираем канат по разрывному усилию Sразр 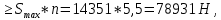 где n = 5,5 – коэффициент запаса прочности. Принимаем канат двойной свивки типа ЛК-Р кончтрукции 6х19 (1 + 6 + 6/6) + 1 о.с. (ГОСТ2688-80) диаметром d = 13 мм и Sразр = 82,95 кН ( 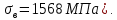 Задача № 4 По данным табл. 4, для свободностоящего крана, грузоподъемностью Q, с постоянным вылетом стрелы L, определить вес противовеса Gпp, реакции в опорах крана. Принять расстояние от оси вращения до центра тяжести: противовеса, lпp = 0,25L; стрелы крана, lстр= 0,3L. Расстояние между опорами принять, h = 0,15QL. Дано: Q = 3,5 тонн, L = 4 м. 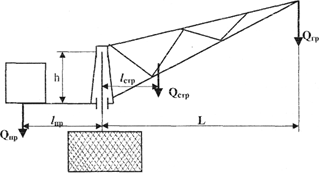 Решение Вес противовеса считается оптимальным при соблюдении условия равенства горизонтальных реакций в опорах нагруженного и ненагруженного крана. Для нагруженного крана 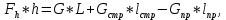 где Fh – горизонтальная реакции в опорах нагруженного крана, Н; h = 0,15QL = 0,15*3,5*4 = 2,1 м – расстояние между опорами; 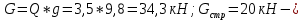 вес поворотной части крана (принимаем). вес поворотной части крана (принимаем).Для ненагруженного крана 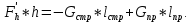 Из условия 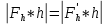 определим вес противовеса определим вес противовесаGпр = 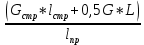 = =  = 92,6 кН. = 92,6 кН. Определим горизонтальные реакции в опорах Fh =  = = 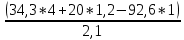 = 32,7 кН. = 32,7 кН.Проверка условия 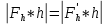  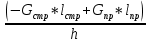 = = 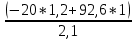 = 32,7 кН. = 32,7 кН.Определим вертикальную реакцию Fv = G + Gстр + Gпр = 34,3 + 20 + 92,6 = 146,9 кН. Задача № 7 Груз, массой Q, находится на максимальном вылете стрелы L. Назначить тип проката, (утолок или швеллер), определить номер профиля для стрелы, укосины и поворотной колонны. Проверить указанные элементы металлоконструкции на прочность. Принять расстояние a = l/5L, масса тележки равна Qт = 0,2Q, режим работы – средний. Дано: Q = 5,5 тс, L = 3,5 м, 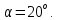 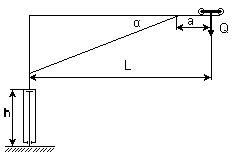 Решение Металлоконструкция крана состоит из поворотной платформы со стрелой и неподвижной колонны. Стрела 1 сварена из сдвоенных швеллеров, по нижним полкам которых перекатывается тележка. Для разгрузки швеллеров стрелы служит укосина 2, состоящая из сдвоенных уголков. Вращающаяся колонна 3 состоит из сдвоенных швеллеров, к которым приварены швеллеры стрелы и уголки укосины. На элементы металлоконструкции действуют наибольшие нагрузки при максимальном вылете стрелы. Определим эквивалентную силу FC, приложенную в точке С, которая находится на расстоянии a = L/5 = 3,5/5 = 0,7 м от конца стрелы. FC = 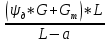 = = 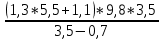 = 101,06 кН. = 101,06 кН.     1 1   A A  C C a a 3 L G + Gт 3 L G + Gт2  B Y B Y            C C    F1 F1 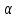 X XF2 FC Методом вырезания узлов находим усилия в стержнях. На узел С действует внешняя сила FC. Тогда относительно координат X и Y можем записать: 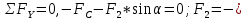 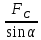 = =  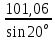 = - 295,5 кН; = - 295,5 кН; 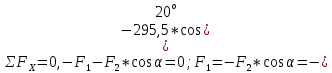 Следовательно, стержень 1 испытывает растяжение, а стержень 2 – сжатие. Пренебрегая напряжением сжатия, определим для стержня 1 момент сопротивления изгибу Wx. Наибольший изгибающий момент в точке С консольной части стрелы определим из выражения 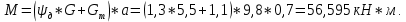 Определим момент сопротивления одного швеллера стержня Wx = 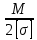 = = 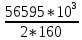 = 177*103 мм3. = 177*103 мм3. Выбираем швеллер №22, для которого Ix = 2110*104 мм4, Wx = 192*103 мм3, A = 2670 мм2, rmax = ix = 88,9 мм, rmin = iy = 23,7 мм. Представим стрелу как двухопорную балку с правой консолью (рис.). Функцию укосины заменяет опора С.  RC = 101,06 кН RC = 101,06 кН      A C F1 = 94,96 кН A C F1 = 94,96 кНRA = 20,2 кН 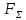 =80,85кН =80,85кН  l1 = 2,8 м l2 = 0,7 м l1 = 2,8 м l2 = 0,7 мРис. Схема нагружения участка стрелы Определим реакции в опорах: RA = 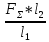 = = 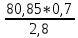 = 20,2 кН; = 20,2 кН;RC = FC = 101,06 кН. Суммарное напряжение, возникающее в сдвоенных швеллерах 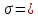  + + 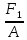 + + 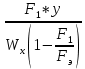 , ,где y – прогиб балки. Эйлерова сила сжатия при потере устойчивости стержня из двух швеллеров Fэ = 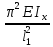 = = 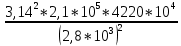 = 11145*103 Н. = 11145*103 Н.Для определения максимального прогиба балки у между опорами воспользуемся универсальными уравнениями изогнутой оси балки 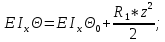 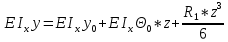 . . За начало координат принимаем левую опору А. Прогиб балки в опорах у = 0 при z = 0 и z = 2,8 м. Тогда второе универсальное уравнение примет вид  При R1 = RA получим  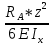 = - = - 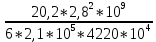 = - 0,003; = - 0,003;При максимальном прогибе балки угол поворота сечения равен нулю. Тогда координату 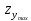 определим из первого универсального уравнения определим из первого универсального уравнения Отсюда получим 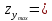 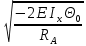 = = 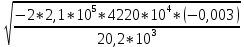 = 1622 мм. = 1622 мм.Тогда для этого сечения запишем  отсюда ymax = 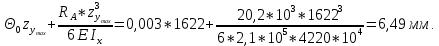 Изгибающий момент в этом сечении  Тогда суммарное напряжение 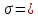 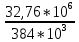 + + 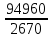 + + 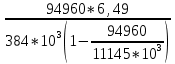 = 122,4 МПа. = 122,4 МПа.что меньше допустимого значения 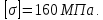 Определим суммарное напряжение в точке С, где прогиб равен нулю 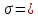  + + 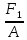 = = 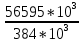 + +  = 165,2 МПа. = 165,2 МПа.Перегрузка стержня 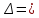  *100% = 3,25%, *100% = 3,25%,что допустимо. Условие прочности для одного уголка укосины имеет вид 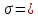 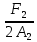 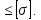 Отсюда получим A2 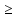 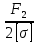 = = 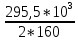 = 923 мм2. = 923 мм2.Принимаем уголок №7, имеющий значение A = 942 мм2. Для вращающейся колонны крана определим размеры опасного сечения только из условия прочности на изгиб по пониженному допустимому напряжению. Изгибающий момент в опасном сечении 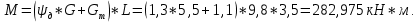 По прочности только на изгиб момент сопротивления колонны составит Wx = 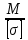 = = 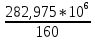 = 1769*103 мм3 = 1769 см3. = 1769*103 мм3 = 1769 см3. Момент сопротивления одного швеллера составляет 884,5 см3. Максимальное значение имеет швеллер №40 (Wx = 761 см3), поэтому принимаем колонну, состоящую из четырех швеллеров №33 (Wx = 484 см3 > 1769/4 = 442 см3). Задача № 18 Определить мощность, необходимую для передвижения тележки с канатной тягой при установившейся скорости. Диаметр ходовых колес Dхк, определить, приняв [р] = 2 МПа (линейный контакт). Диаметр цапфы dц = 0,3Dхк, коэффициент трения в подшипниках fп = 0,02. Массу тележки mт = 0,1Q, Значения массы поднимаемого груза Q, скорость передвижения кран-балки Vм, коэффициент трения качения колеса µ, приведены в табл.15. Дано: V = 0,4 м/с, Q = 2,5 тонн, 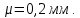 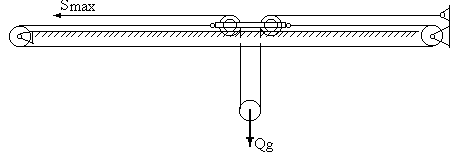 Решение Определим нагрузку на одно колесо тележки Rmax = 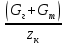 = = 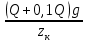 = =  = = 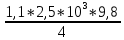 = 6738 Н. = 6738 Н.Определим диаметр ходового колеса тележки 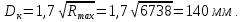 Принимаем Dк = 160 мм и выполним проверку по напряжениям при линейном контакте 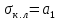 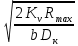  (для стали Ст35), (для стали Ст35),где а1 = 190 – коэффициент пропорциональности для стальных колес; Kv = 1 + 0,2V = 1 + 0,2*0,4 = 1,08 – коэффициент влияния скорости. 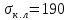 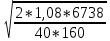 = 286 МПа < 450 МПа. = 286 МПа < 450 МПа.Условие по допускаемым напряжениям при линейном контакте выполняются. Тележка с канатной тягой имеет относительно небольшие массу и габаритные размеры, а потому в режимах разгона и торможения возникают незначительные инерционные нагрузки, которыми можно пренебречь. В установившемся режиме сопротивление передвижению тележки определяется из выражения Wу = Wтр + Wк, где Wтр – сопротивление от сил трения в ходовых частях тележки; Wк – сопротивление от разности усилий в ветвях грузового каната. Wтр =  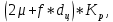 где Кр = 1,5 – коэффициент трения реборд о головку рельса. Wк = 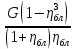 . .Тогда получим Wу =  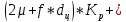 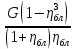 = =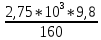 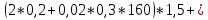 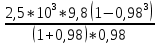 = =1086 Н. Тогда требуемая мощность двигателя в установившемся режиме P = 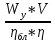 = = 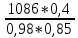 = 521 Вт. = 521 Вт.Задача № 20 Определить мощность электродвигателя для привода ленточного транспортера, если известны (табл. 17): производительность Q; скорость ленты V; длина транспортера L; угол наклона транспортера β. Транспортируемый материал – зерно, удельная масса γ = 0,8 т/м3; коэффициент сопротивления передвижению ленты по роликам w = 0,45. Дано: Q = 75 т/час, V = 4,0 м/с, L = 15 м, 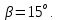 Решение Энергия привода ленточного конвейера расходуется на выполнение полезной работы и преодоление сопротивлений, основным из которых является сопротивление передвижению ленты. С определенными упрощениями сопротивления на прямолинейных участках можно рассчитать по следующим формулам: Для рабочей ветви: Wр=g∙Lн∙[(qг + qл + qр.р)∙w∙Cosβ + (qг + qл)∙Sinβ]; Для холостой ветви Wх = g∙Lх∙(qг+ qр.ᵪ)∙(w∙Cosβ-Sinβ), где g = 9,81 м/с²- ускорение свободного падения; Lн и Lх - длины рассматриваемых рабочего и холостого прямолинейных участков конвейера; qг, qл, qр.р, qр.х - линейные плотности соответственно груза, ленты, роликовых опор рабочей и холостой ветви; qр.р = mр.р/ lр, qр.х = mр.х/ lх; w- коэффициент сопротивления движению ленты по роликам. Определим ширину ленты с учетом придания рабочей ветви желобчатой формы посредством трехроликовой опоры при секундной производительности Qс = Q/3,6 = 75/3,6 = 20,8 кг/с и коэффициентах Kп = 0,085, Kᵦ = 0,8 (при β = 15º) B = 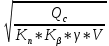 = =  = 0,309 м. = 0,309 м.Принимаем В = 320 мм. Выбираем резинотканевую ленту с прокладками из ткани БКНЛ-65( с основой и утком из комбинированных нитей): предел прочности ткани Кр = 65Н/мм; число (предварительное) прокладок z = 3; толщина прокладок δₒ = 1,15мм; толщина обрезиненного слоя см рабочей стороны δ1 = 2мм (ввиду малой абразивности зерна), с опорной стороны δ2 = 1мм. С целью защиты от механических повреждений и влаги ленту покрывают слоем резины. Толщина слоя резины с рабочей стороны ленты δ1 = 1,5..6мм, с опорной- δ2 = 1…2мм. Общая толщина ленты Δ = δₒ∙z + δ1 + δ2, где δₒ - толщина одной прокладки, z - число прокладок. Δ = δₒ∙z + δ1 + δ2 = 1,15∙3 + 2 + 1 = 6,45мм. Линейная плотность ленты qᴫ = 1,12∙B∙δ где 1,12 - среднее значение массы 1м² ленты толщиной 1мм; B - ширина ленты, м. qᴫ = 1,12∙B∙δ = 1,12∙0,320∙6,45 = 2,3 кг/м. Линейная плотность груза qг = Q⁄(3,6∙V) = 75⁄(3,6∙4,0) = 5,2 кг/м. При B = 320 мм и V= 4,0 м/с для рабочей ветви принимаем диаметр роликов dр = 108 мм. С целью увеличения долговечности ленты и создания более благоприятных условий ее работы угол наклона боковых роликов α = 30º. Тогда масса вращающихся частей трехроликовой опоры mр.р = 12кг. Масса ролика для холостой ветви mр.х = 9,8кг. С учетом ширины ленты и желобчатой формы рабочей ветви принимем расстояния между роликами: рабочей ветви lр = 1,5м, холостой ветви lх = 3м. Линейная плотность рабочей ветви роликовой опоры qр.р = mр.р/ lр = 12/1,5 = 8 кг/м, холостой ветви qр.х = mр.х/ lх = 9,8/3 = 3,3 кг/м. Тогда получим Wр = 9,81∙15∙[(5,2 + 2,3 + 8)∙0,45∙Cos15o + (5,2 + 2,3)∙Sin15o] = 1277 H; Wх = 9,81∙15∙(5,2+ 3,3)∙(0,45∙Cos15o – Sin15o) = 220 H. Чтобы ленту привести в движение необходимо создать тяговое усилие Ft (окружную силу барабана), которое обычно определяют методом обхода по контуру. При этом весь контур разбивают на участки и, последовательно определяют натяжение для каждого участка. В нашем случае натяжение тягового органа в каждом последующем участке равно натяжению в предыдущем плюс сумма сопротивлений на рассматриваемом участке. В результате получают Ft= ξ̥ᵐ∙∑W, где m- число барабанов, кроме приводного; ∑W – алгебраическая сумма сопротивлений на прямолинейных участках. Принимаем коэффициент сопротивления передвижению ленты на криволинейных участках в среднем ξ̥ =1,05. Тогда 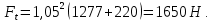 Для определения мощности электродвигателя для привода ленточного транспортера необходимо знать расчетную (потребную) мощность Рдв = Ft·V/(ƞб·ƞм), где 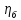 - КПД барабана, зависящий от типа подшипников, жесткости ленты и пр., ƞб ≈ 0,92..0,96; - КПД барабана, зависящий от типа подшипников, жесткости ленты и пр., ƞб ≈ 0,92..0,96;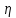 м - КПД передаточного механизма (принимаем м - КПД передаточного механизма (принимаем 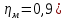 . . Следовательно, потребная мощность составит Рдв =  = 7719 Вт. = 7719 Вт.Для рассчитываемого конвейера можно применить электродвигатель 4А132S4УЗ с номинальной мощностью Рном = 7,5 кВт и номинальной частотой вращения вала nдв = nном = 1445 мин-1. Перегрузка составляет 2,9% < 5%, что допустимо. |
