20 Вариант МОР. Решение Сформулируем экономическоматематическую модель задачи
 Скачать 231.28 Kb. Скачать 231.28 Kb.
|
Задание № 4Условие: Решение задачи о назначениях. На предприятии необходимо выполнить последовательно 12 видов работ (R1÷R12). 12 сотрудников предприятия (S1÷S12) затрачивают на выполнение каждого вида работ различное время в часах, таблица 5. Распределить работников по видам работ так, чтобы общее время на выполнение работ было минимально. Очередность выполнения работ не имеет значения. Составить экономико-математическую модель задачи и решить задачу, применив венгерский алгоритм. Таблица 5 - Исходные данные
Решение: Запишем экономико-математическую модель для нашей задачи. Переменные xij принимают значения 1, если i-й кандидат занимает j-ю вакансию. Если данное условие не выполняется, то xij=0. Ограничения по сотрудникам: x11 + x12 + x13 + x14 + x15 = 1 x21 + x22 + x23 + x24 + x25 = 1 x31 + x32 + x33 + x34 + x35 = 1 x41 + x42 + x43 + x44 + x45 = 1 x51 + x52 + x53 + x54 + x55 = 1 Ограничения по времени: x11 + x21 + x31 + x41 + x51 = 1 x12 + x22 + x32 + x42 + x52 = 1 x13 + x23 + x33 + x43 + x53 = 1 x14 + x24 + x34 + x44 + x54 = 1 x15 + x25 + x35 + x45 + x55 = 1 Целевая функция: 14x11 + 10x12 + 12x13 + 13,5x14 + 8x15 + 15x21 + 9,5x22 + 15x23 + 14x24 + 7,5x25 + 18x31 + 9,75x32 + 16x33 + 15x34 + 7x35 + 14x41 + 10x42 + 15,5x43 + 15,5x44 + 7x45 + 13x51 + 10x52 + 15,5x53 + 14x54 + 7,5x55 → min Найдем минимальный элемент каждого столбца и запишем снизу матрицы: 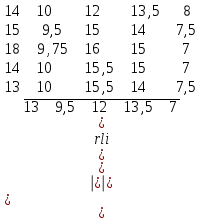
Из всех элементов каждого столбца вычитаем минимальный элемент этого столбца: 
Найдем минимальный элемент каждой строки и запишем на правой стороне строки: 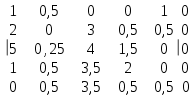
Вычтем из каждого элемента матрицы минимальный элемент соотвествующей строки:  Отмечаем произвольный нуль в первом столбце звездой. Затем просматриваем второй столбец и, если в нем есть нуль и в этой строке нет отмеченного нуля, то отмечаем данный нулевой элемент звездочкой. Аналогично поступаем с остальными столбцами: 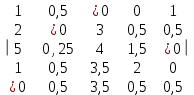 Вычиcляем количество отмеченных нулей и если количество отмеченных нулей равно размеру матрицы, то найдено оптимальное решение. В нашем случае количество отмеченных нулей равно 4. 4<5. Переходя по столбцам обнаруживаем невыделенный нуль и строка, содержащая этот нуль, содержит также нуль со звездой. Обнаруженный нуль отмечаем знаком °. 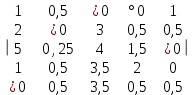
Невыделенных нулей нет. Найдем минимальный элемент среди невыделенных чисел: min{3, 0.5, 4, 1.5, 3.5, 2, 3.5, 0.5}=0.5 Вычитаем найденное минимальное число из всех невыделенных чисел и прибавим его ко всем числам, стоящих на пересечении выделенных строк и столбцов.  Переходя по столбцам обнаруживаем невыделенный нуль и строка, содержащая этот нуль, содержит также нуль со звездой. Обнаруженный нуль отмечаем знаком °.  Невыделенных нулей нет. Найдем минимальный элемент среди невыделенных чисел: min{5, 0.25, 3.5, 1, 1, 0.5, 3, 1.5}=0.25 Вычитаем найденное минимальное число из всех невыделенных чисел и прибавим его ко всем числам, стоящих на пересечении выделенных строк и столбцов. 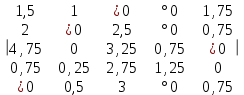 Переходя по столбцам обнаруживаем невыделенный нуль и строка, содержащая этот нуль, содержит также нуль со звездой. Обнаруженный нуль отмечаем знаком °. 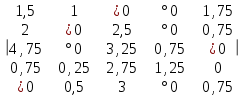 Исходя из нуля со знаком °, в строке которого нет нуля со звездой, строим следующую цепочку элементов (4,5), (3,5), (3,2), (2,2), (2,4). Цепочка образуется движением от 0° к 0* по столбцу и от 0* к 0° по строке. Над элементами цепочки стоящими на нечетных местах ( 0°) ставим *. Уничтожаем ° над элементами, стояoими на четных местах цепочки. Уничтожаем все ° над нулями и снимаем все горизонтальные и вертикальные выделения: 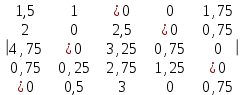 Вычиcляем количество отмеченных нулей и если количество отмеченных нулей равно размеру матрицы, то найдено оптимальное решение. В нашем случае количество отмеченных нулей равно 5. Следовательно найдено оптимальное решение. Оптимальное распределение: (5, 1), (1, 3), (4, 5), (3, 2), (2, 4) Суммарное распределение: 13+12+7+9.75+14=55.75 При этом следует: Назначить 5-го работника на 1-ю работу. Назначить 1-го работника на 3-ю работу. Назначить 4-го работника на 5-ю работу. Назначить 3-го работника на 2-ю работу. Назначить 2-го работника на 4-ю работу. Список использованных источниковПродюсерство. Экономико-математические методы и модели: Учебное пособие / Под ред. Ю.В. Криволуцкого, Л.А. Фунберг. - М.: Юнити, 2015. - 319 c. Макаров, С.И. Методы оптимальных решений (экономико-математические методы и модели)(для бакалавров) / С.И. Макаров. - М.: КноРус, 2016. - 416 c Орлова, И.В. Экономико-математические методы и модели: компьютерное моделирование: Учебное пособие / И.В. Орлова, В.А. Половников. - М.: Вузовский учебник, 2017. - 344 c. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
