20 Вариант МОР. Решение Сформулируем экономическоматематическую модель задачи
 Скачать 231.28 Kb. Скачать 231.28 Kb.
|
|
Содержание Задание № 1 2 Задание № 2 7 Задание № 3 9 Задание № 4 22 Список использованных источников 28 Задание № 1Условие: Составить математическую модель задачи своего варианта и решить графическим методом и симплекс-методом (MS Excel) Фабрика выпускает два вида красок: для внутренних (I) и для внешних (Е) работ. Для производства красок используются два исходных продукта – А и В. Расходы А и В на одну тонну соответствующих красок и суточные запасы продуктов приведены в таблице 1. Таблица 1 – Исходные данные
Цены одной тонны красок равны 3 у.е. для краски Е и 2 у.е. для краски I. Какое количество краски каждого вида нужно производить, чтобы доход был максимальным? Решение: Сформулируем экономическо-математическую модель задачи. Обозначим через x1 количество краски для наружных работ (в тоннах), x2 – количество краски для внутренних работ (в тоннах). Необходимо максимизировать доход от реализации краски: Математическая модель поставленной задачи имеет следующий вид [2, c. 315]:  Решим данную задачу графическим способом. Построим область допустимых решений, т.е. решим графически систему неравенств. Построим уравнение x1+2x2 = 6 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 3. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 6. Соединяем точку (0;3) с (6;0) прямой линией. Построим уравнение 2x1+x2 = 8 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 8. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 4. Соединяем точку (0;8) с (4;0) прямой линией. На рисунке 1 представлены прямые. 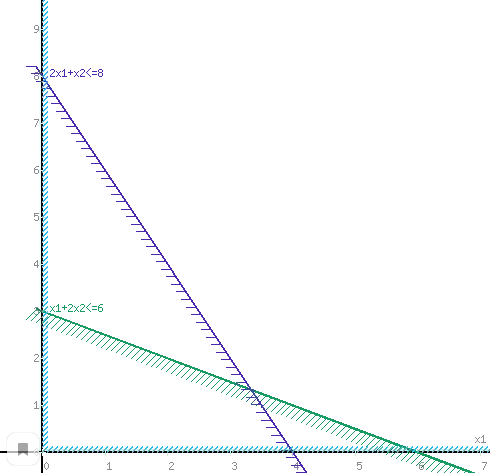 Рисунок 1 - Прямые Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений, рисунок 2. Рассмотрим целевую функцию задачи F = 3x1+2x2 → max. Построим прямую, отвечающую значению функции F = 3x1+2x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (3;2). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На рисунке 2 эта прямая обозначена пунктирной линией.  Рисунок 2 – Многоугольник решений Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых, то ее координаты удовлетворяют уравнениям этих прямых: 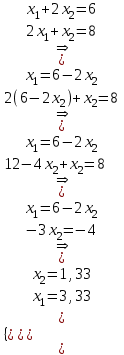 Откуда найдем максимальное значение целевой функции: F(x) = 3*3,33 + 2*1,33 = 12,67 Решим данную задачу с помощью MS Excel. Введем исходные данные, рисунок 3.  Рисунок 3 – Исходные данные Введем зависимости для целевой функции и ограничений, рисунок 4. 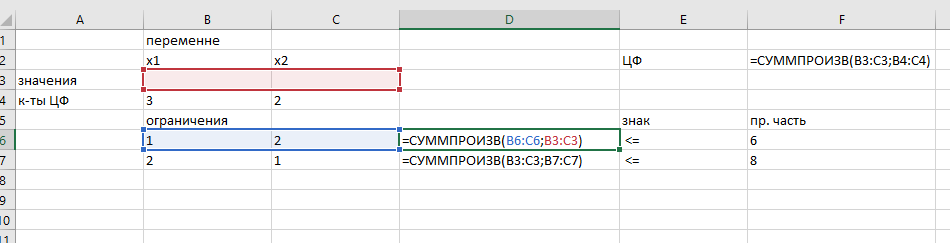 Рисунок 4 – Зависимости Решим данную задачу с помощью Поиск решения, рисунок 5. 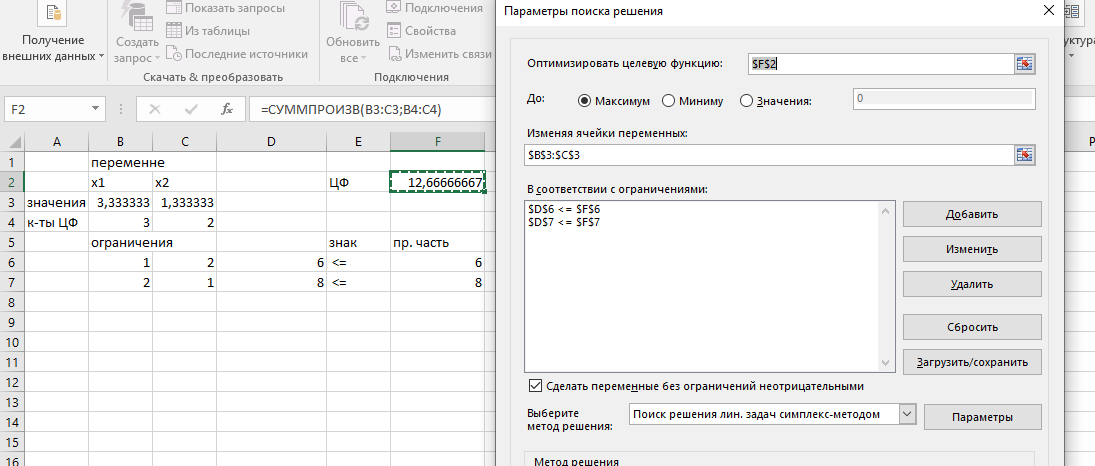 Рисунок 5 – Поиск решения Таким образом, для максимизации прибыли необходимо производить краски вида Е – 3,33 т, краски вида I – 1,33 т. Прибыль составит 12,67 д.ед. Ответ: F(x)max=12,67; x1=3,33; x2=1,33 | |||||||||||||||||
