20 Вариант МОР. Решение Сформулируем экономическоматематическую модель задачи

• Название: Решение Сформулируем экономическоматематическую модель задачи
• Дата: 26.11.2022
• Размер: 231.28 Kb.
• Имя файла: 20 Вариант МОР.docx
• Тип: Документы; #812851
• страница: 2 из 3

Задание № 2

Условие:

Составить задачу, двойственную задаче задания №1, дать содержательную интерпретацию.
Решение:

Составим двойственную задачу.

F(Z)=6y₁+8y₂

Ограничения:



При решении задачи в MS Excel выведем отчет об устойчивости, рисунок 6.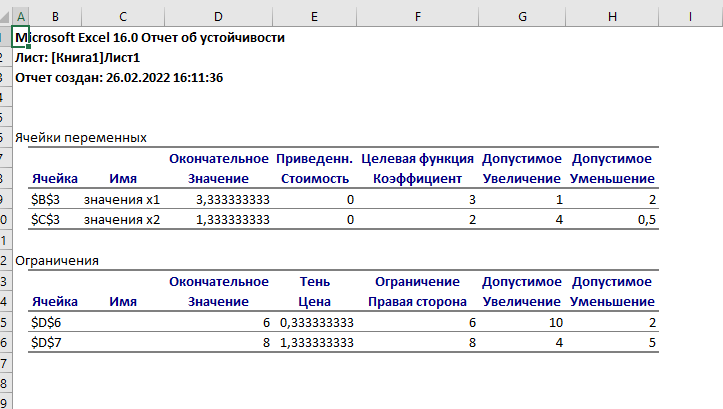


Рисунок 6 – Отчет об устойчивости
Оптимальный план двойственной задачи.
y₁=0,33, y₂=1,33.

F(Z)=6*0,33+8*1,33=12,67

Подставим оптимальный план прямой задачи в систему ограниченной математической модели:

1*3,33 + 2*1,33= 6 = 6

2*3,33 + 1*1,33 = 8 = 8

1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₁ ≠ 0).

2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₂ ≠ 0).

При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:

1*0,33 + 2*1,33 = 3 = 3

2*0,33+ 1*1,33 = 2 = 2

1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-й продукт экономически выгодно производить (убытки от производства этого вида продукции отсутствуют), а его использование предусмотрено оптимальным планом прямой задачи (x₁>0).

2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-й продукт экономически выгодно производить (убытки от производства этого вида продукции отсутствуют), а его использование предусмотрено оптимальным планом прямой задачи (x₂>0).

Задание № 3

Условие:

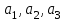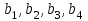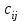На трех заводах производится однородная продукции в количестве единиц. Четырем потребителям требуется соответственно единиц продукции. Расходы по перевозке единицы продукции с i-го завода j-му потребителю известны (см. Транспортную таблицу 2). Требуется спланировать перевозку продукции так, чтобы затраты на транспортировку были минимальными.

1) Записать математическую модель транспортной задачи.

2) Найти опорное решение методом наименьшей стоимости и северо-западного угла.

3) Опорное решение проверить методом потенциалов, получить оптимальное решение.
Таблица 2 - Транспортная таблица

Заводы	Потребители				Запас продукции, ед.
	В1	В2	В3	В4
А1	3	6	4	7	800
А2	2	5	8	4	300
А3	3	7	4	9	600
Потребность в продукции, ед.	400	450	350	500

Решение:

Запишем экономико-математическую модель для нашей задачи.
Переменные:

x₁₁ – количество груза из 1-го завода для 1-ого потребителя.

x₁₂ – количество груза из 1-го завода для 2-ого потребителя.

x₁₃ – количество груза из 1-го завода для 3-его потребителя.

x₁₄ – количество груза из 1-го завода для 4-ого потребителя.

x₂₁ – количество груза из 2-го завода для 1-ого потребителя.

x₂₂ – количество груза из 2-го завода для 2-ого потребителя.

x₂₃ – количество груза из 2-го завода для 3-его потребителя.

x₂₄ – количество груза из 2-го завода для 4-ого потребителя.

x₃₁ – количество груза из 3-го завода для 1-ого потребителя.

x₃₂ – количество груза из 3-го завода для 2-ого потребителя.

x₃₃ – количество груза из 3-го завода для 3-его потребителя.

x₃₄ – количество груза из 3-го завода для 4-ого потребителя.

Ограничения по запасам:

x₁₁ + x₁₂ + x₁₃ + x₁₄ ≤ 800 (для 1 завода)

x₂₁ + x₂₂ + x₂₃ + x₂₄ ≤ 300 (для 2 завода)

x₃₁ + x₃₂ + x₃₃ + x₃₄ ≤ 600 (для 3 завода)

Ограничения по потребностям:

x₁₁ + x₂₁ + x₃₁ = 400 (для 1-го потребителя)

x₁₂ + x₂₂ + x₃₂ = 450 (для 2-го потребителя)

x₁₃ + x₂₃ + x₃₃ = 350 (для 3-го потребителя)

x₁₄ + x₂₄ + x₃₄ = 500 (для 4-го потребителя)

Целевая функция:

3x₁₁ + 6x₁₂ + 4x₁₃ + 7x₁₄ + 2x₂₁ + 5x₂₂ + 8x₂₃ + 4x₂₄ + 3x₃₁ + 7x₃₂ + 4x₃₃ + 9x₃₄ → min

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 800 + 300 + 600 = 1700

∑b = 400 + 450 + 350 + 500 = 1700

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Искомый элемент равен c₂₁=2. Для этого элемента запасы равны 300, потребности 400. Поскольку минимальным является 300, то вычитаем его.

x₂₁ = min(300,400) = 300.

Искомый элемент равен c₁₁=3. Для этого элемента запасы равны 800, потребности 100. Поскольку минимальным является 100, то вычитаем его.

x₁₁ = min(800,100) = 100.

Искомый элемент равен c₁₃=4. Для этого элемента запасы равны 700, потребности 350. Поскольку минимальным является 350, то вычитаем его.

x₁₃ = min(700,350) = 350.

Искомый элемент равен c₁₂=6. Для этого элемента запасы равны 350, потребности 450. Поскольку минимальным является 350, то вычитаем его.

x₁₂ = min(350,450) = 350.

Искомый элемент равен c₃₂=7. Для этого элемента запасы равны 600, потребности 100. Поскольку минимальным является 100, то вычитаем его.

x₃₂ = min(600,100) = 100.

Искомый элемент равен c₃₄=9. Для этого элемента запасы равны 500, потребности 500. Поскольку минимальным является 500, то вычитаем его.

x₃₄ = min(500,500) = 500.

Запишем полученный опорный план, таблица 3.
Таблица 3 – Опорный план

	B1	B2	B3	B4	Запасы
A1	3[100]	6[350]	4[350]	7	800
A2	2[300]	5	8	4	300
A3	3	7[100]	4	9[500]	600
Потребности	400	450	350	500

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 3*100 + 6*350 + 4*350 + 2*300 + 7*100 + 9*500 = 9600

Используя метод северо-западного угла, построим первый опорный план транспортной задачи.

План начинается заполняться с верхнего левого угла.

Искомый элемент равен c₁₁=3. Для этого элемента запасы равны 800, потребности 400. Поскольку минимальным является 400, то вычитаем его.

x₁₁ = min(800,400) = 400.

Искомый элемент равен c₁₂=6. Для этого элемента запасы равны 400, потребности 450. Поскольку минимальным является 400, то вычитаем его.

x₁₂ = min(400,450) = 400.

Искомый элемент равен c₂₂=5. Для этого элемента запасы равны 300, потребности 50. Поскольку минимальным является 50, то вычитаем его.

x₂₂ = min(300,50) = 50.

Искомый элемент равен c₂₃=8. Для этого элемента запасы равны 250, потребности 350. Поскольку минимальным является 250, то вычитаем его.

x₂₃ = min(250,350) = 250.

Искомый элемент равен c₃₃=4. Для этого элемента запасы равны 600, потребности 100. Поскольку минимальным является 100, то вычитаем его.

x₃₃ = min(600,100) = 100.

Искомый элемент равен c₃₄=9. Для этого элемента запасы равны 500, потребности 500. Поскольку минимальным является 500, то вычитаем его.

x₃₄ = min(500,500) = 500.

В таблице 4 представлен опорный план.
Таблица 4 – Опорный план

	B1	B2	B3	B4	Запасы
A1	3[400]	6[400]	4	7	800
A2	2	5[50]	8[250]	4	300
A3	3	7	4[100]	9[500]	600
Потребности	400	450	350	500

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 3*400 + 6*400 + 5*50 + 8*250 + 4*100 + 9*500 = 10750

Так как значение целевой функции для опорного плана, найденного по минимальной стоимости, меньше чем значение целевой функции, найденной по северо-западному углу, то в качестве оптимального плана выбираем опорный план, найденный по наименьшей стоимости.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₂ + v₁ = 2; 3 + u₂ = 2; u₂ = -1

u₁ + v₂ = 6; 0 + v₂ = 6; v₂ = 6

u₃ + v₂ = 7; 6 + u₃ = 7; u₃ = 1

u₃ + v₄ = 9; 1 + v₄ = 9; v₄ = 8

u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4

	v1=3	v2=6	v3=4	v4=8
u1=0	3[100]	6[350]	4[350]	7
u2=-1	2[300]	5	8	4
u3=1	3	7[100]	4	9[500]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;4): 0 + 8 > 7;

(2;4): -1 + 8 > 4;

(3;1): 1 + 3 > 3;

(3;3): 1 + 4 > 4;

Вычисляем оценки свободных клеток:

d₁₄ = 0 + 8 - 7 = 1 > 0

d₂₄ = -1 + 8 - 4 = 3 > 0

d₃₁ = 1 + 3 - 3 = 1 > 0

d₃₃ = 1 + 4 - 4 = 1 > 0

max(1,3,1,1) = 3

Выбираем максимальную оценку свободной клетки (2;4): 4

Для этого в перспективную клетку (2;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	3[100][+]	6[350][-]	4[350]	7	800
2	2[300][-]	5	8	4[+]	300
3	3	7[100][+]	4	9[500][-]	600
Потребности	400	450	350	500

Цикл приведен в таблице (2,4 → 2,1 → 1,1 → 1,2 → 3,2 → 3,4).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 1) = 300. Прибавляем 300 к объемам грузов, стоящих в плюсовых клетках и вычитаем 300 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план, таблица 5.
Таблица 5 – Новый опорный план

	B1	B2	B3	B4	Запасы
A1	3[400]	6[50]	4[350]	7	800
A2	2	5	8	4[300]	300
A3	3	7[400]	4	9[200]	600
Потребности	400	450	350	500

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₁ + v₂ = 6; 0 + v₂ = 6; v₂ = 6

u₃ + v₂ = 7; 6 + u₃ = 7; u₃ = 1

u₃ + v₄ = 9; 1 + v₄ = 9; v₄ = 8

u₂ + v₄ = 4; 8 + u₂ = 4; u₂ = -4

u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4

	v1=3	v2=6	v3=4	v4=8
u1=0	3[400]	6[50]	4[350]	7
u2=-4	2	5	8	4[300]
u3=1	3	7[400]	4	9[200]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;4): 0 + 8 > 7;

(3;1): 1 + 3 > 3;

(3;3): 1 + 4 > 4;

d₁₄ = 0 + 8 - 7 = 1 > 0

d₃₁ = 1 + 3 - 3 = 1 > 0

d₃₃ = 1 + 4 - 4 = 1 > 0

max(1,1,1) = 1

Выбираем максимальную оценку свободной клетки (1;4): 7

Для этого в перспективную клетку (1;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	3[400]	6[50][-]	4[350]	7[+]	800
2	2	5	8	4[300]	300
3	3	7[400][+]	4	9[200][-]	600
Потребности	400	450	350	500

Цикл приведен в таблице (1,4 → 1,2 → 3,2 → 3,4).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 2) = 50. Прибавляем 50 к объемам грузов, стоящих в плюсовых клетках и вычитаем 50 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план, таблица 6.
Таблица 6 – Новый опорный план

	B1	B2	B3	B4	Запасы
A1	3[400]	6	4[350]	7[50]	800
A2	2	5	8	4[300]	300
A3	3	7[450]	4	9[150]	600
Потребности	400	450	350	500

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4

u₁ + v₄ = 7; 0 + v₄ = 7; v₄ = 7

u₂ + v₄ = 4; 7 + u₂ = 4; u₂ = -3

u₃ + v₄ = 9; 7 + u₃ = 9; u₃ = 2

u₃ + v₂ = 7; 2 + v₂ = 7; v₂ = 5

	v1=3	v2=5	v3=4	v4=7
u1=0	3[400]	6	4[350]	7[50]
u2=-3	2	5	8	4[300]
u3=2	3	7[450]	4	9[150]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(3;1): 2 + 3 > 3;

(3;3): 2 + 4 > 4;

d₃₁ = 2 + 3 - 3 = 2 > 0

d₃₃ = 2 + 4 - 4 = 2 > 0

max(2,2) = 2

Выбираем максимальную оценку свободной клетки (3;1): 3

Для этого в перспективную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	3[400][-]	6	4[350]	7[50][+]	800
2	2	5	8	4[300]	300
3	3[+]	7[450]	4	9[150][-]	600
Потребности	400	450	350	500

Цикл приведен в таблице (3,1 → 3,4 → 1,4 → 1,1).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 4) = 150. Прибавляем 150 к объемам грузов, стоящих в плюсовых клетках и вычитаем 150 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план, таблица 7.
Таблица 7 – Новый опорный план

	B1	B2	B3	B4	Запасы
A1	3[250]	6	4[350]	7[200]	800
A2	2	5	8	4[300]	300
A3	3[150]	7[450]	4	9	600
Потребности	400	450	350	500

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₃ + v₁ = 3; 3 + u₃ = 3; u₃ = 0

u₃ + v₂ = 7; 0 + v₂ = 7; v₂ = 7

u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4

u₁ + v₄ = 7; 0 + v₄ = 7; v₄ = 7

u₂ + v₄ = 4; 7 + u₂ = 4; u₂ = -3

	v1=3	v2=7	v3=4	v4=7
u1=0	3[250]	6	4[350]	7[200]
u2=-3	2	5	8	4[300]
u3=0	3[150]	7[450]	4	9

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;2): 0 + 7 > 6;

d₁₂ = 0 + 7 - 6 = 1 > 0

Выбираем максимальную оценку свободной клетки (1;2): 6

Для этого в перспективную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	3[250][-]	6[+]	4[350]	7[200]	800
2	2	5	8	4[300]	300
3	3[150][+]	7[450][-]	4	9	600
Потребности	400	450	350	500

Цикл приведен в таблице (1,2 → 1,1 → 3,1 → 3,2).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 1) = 250. Прибавляем 250 к объемам грузов, стоящих в плюсовых клетках и вычитаем 250 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план, таблица 8.
Таблица 8 – Новый опорный план

	B1	B2	B3	B4	Запасы
A1	3	6[250]	4[350]	7[200]	800
A2	2	5	8	4[300]	300
A3	3[400]	7[200]	4	9	600
Потребности	400	450	350	500

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₂ = 6; 0 + v₂ = 6; v₂ = 6

u₃ + v₂ = 7; 6 + u₃ = 7; u₃ = 1

u₃ + v₁ = 3; 1 + v₁ = 3; v₁ = 2

u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4

u₁ + v₄ = 7; 0 + v₄ = 7; v₄ = 7

u₂ + v₄ = 4; 7 + u₂ = 4; u₂ = -3

	v1=2	v2=6	v3=4	v4=7
u1=0	3	6[250]	4[350]	7[200]
u2=-3	2	5	8	4[300]
u3=1	3[400]	7[200]	4	9

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(3;3): 1 + 4 > 4;

d₃₃ = 1 + 4 - 4 = 1 > 0

Выбираем максимальную оценку свободной клетки (3;3): 4

Для этого в перспективную клетку (3;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	3	6[250][+]	4[350][-]	7[200]	800
2	2	5	8	4[300]	300
3	3[400]	7[200][-]	4[+]	9	600
Потребности	400	450	350	500

Цикл приведен в таблице (3,3 → 3,2 → 1,2 → 1,3).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 2) = 200. Прибавляем 200 к объемам грузов, стоящих в плюсовых клетках и вычитаем 200 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план, таблица 9.
Таблица 9 – Новый опорный план

	B1	B2	B3	B4	Запасы
A1	3	6[450]	4[150]	7[200]	800
A2	2	5	8	4[300]	300
A3	3[400]	7	4[200]	9	600
Потребности	400	450	350	500

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₂ = 6; 0 + v₂ = 6; v₂ = 6

u₁ + v₃ = 4; 0 + v₃ = 4; v₃ = 4

u₃ + v₃ = 4; 4 + u₃ = 4; u₃ = 0

u₃ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₁ + v₄ = 7; 0 + v₄ = 7; v₄ = 7

u₂ + v₄ = 4; 7 + u₂ = 4; u₂ = -3

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.

Минимальные затраты составят:

F(x) = 6*450 + 4*150 + 7*200 + 4*300 + 3*400 + 4*200 = 7900

Из 1-го завода необходимо груз направить 2-ому потребителю (450 ед.), 3-ему потребителю (150 ед.), 4-ому потребителю (200 ед.)

Из 2-го завода необходимо весь груз направить 4-ому потребителю.

Из 3-го завода необходимо груз направить 1-ому потребителю (400 ед.), 3-ему потребителю (200 ед.)