Отчет по лабораторной работе 2 по дисциплине Методы анализа динамических систем
 Скачать 347.78 Kb. Скачать 347.78 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Дальневосточный федеральный университет»
Кафедра электроэнергетики и электротехники ОТЧЕТ по лабораторной работе №2 по дисциплине «Методы анализа динамических систем» на тему «Устойчивость замкнутых САР» Выполнил студент гр. Б3117-13.03.02ээсс А.И. Никифоров Проверил преподаватель, к.т.н. К.В. Чупина ____________________________ (зачет/незачет) «___» ____________2019 г. г. Владивосток 2019 Цель работы: анализ устойчивости САР по алгебраическим критериям устойчивости и исследование влияния характера расположения корней на комплексной плоскости на величину запаса устойчивости САР. Вывод передаточной функции замкнутой САР Таблица 1 – Исходные данные.
 Рисунок 1 – Замкнутая структурная схема с единичной отрицательной обратной связью Передаточная функция разомкнутой САР:  тогда:  Знаменатель и является характеристическим уравнением. Найдем неизвестную величину  : :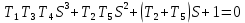 Расчет искомого параметра, при котором замкнутая система находится на границе устойчивости. Согласно критерию Гурвица: 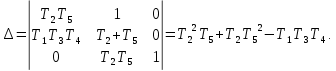 Решим полученное уравнение относительно  и получим, что: и получим, что: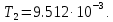 3. Графики переходных процессов для устойчивой, неустойчивой и находящейся на границе устойчивости САР.  Рисунок 2 – График переходного процесса для устойчивой САР  Рисунок 3 – График переходного процесса для неустойчивой САР  Рисунок 4 – График переходного процесса для находящейся на границе устойчивости САР 4. Расположение корней характеристического уравнения на комплексной плоскости для устойчивой, неустойчивой и находящейся на границе устойчивости САР. Имея характеристическое уравнение:  найдем его корни и расположение на комплексной плоскости, используя найденную величину  . .   Отобразим их на комплексной плоскости:  Рисунок 5 – Корни характеристического уравнения для устойчивой САР Корни для неустойчивой САР при  : :   Их расположение: 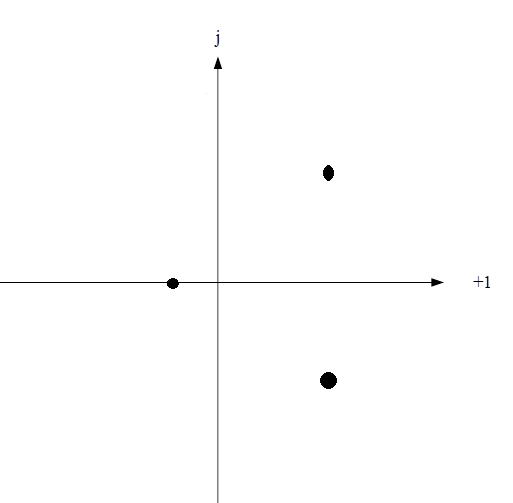 Рисунок 6 – Расположение корней неустойчивой САР на комплексной плоскости И соответственно корни для САР на границе устойчивости:   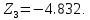  Рисунок 7 – Расположение корней САР на границе устойчивости Вывод: в данной лабораторной был проведен анализ устойчивости САР по критерию устойчивости Гурвица и влияния характера расположения корней на комплексной плоскости. По данным графикам можно сделать вывод, если хотя бы один корень характеристического уравнения имеет положительную действительную часть, то данная САР является неустойчивой. Для устойчивости САР необходимо, чтобы все корни имели отрицательную действительную часть, и чем дальше их расположение от начала координат, тем больше запас устойчивости САР. |
