НПИС. Лекция+14-15. Анализ устойчивости систем автоматического регулирования

• Название: Анализ устойчивости систем автоматического регулирования
• Дата: 26.12.2021
• Размер: 1.38 Mb.
• Имя файла: Лекция+14-15.doc
• Тип: Документы; #318932

3 АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО

РЕГУЛИРОВАНИЯ

3.1 Понятие устойчивости
Одно из основных требований к САР – быть устойчивой. САР называется устойчивой, если она, будучи выведена из равновесия каким-либо воздействием, самостоятельно возвращается к положению равновесия после прекращения этого воздействия.

В устойчивых САР отклонение регулируемой величины от равновесного значения с течением времени апериодически или колебательно стремится к нулю (рисунок. 3.1, а). В неустойчивых САР отклонение регулируемой величины от равновесного значения апериодически или колебательно возрастает (рисунок 3.1, б). Если в системе устанавливается постоянная величина отклонения или колебания носят незатухающий характер (рисунок 3.1, в), то система находится на границе устойчивости, система нейтральна.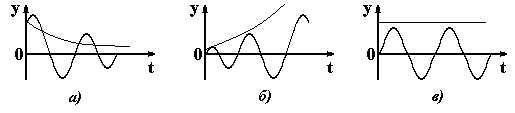

Рисунок 3.1

3.2 Анализ устойчивости по корням характеристического уравнения
В линейных САР изменение выходной переменной y(t) под влиянием воздействия x(t) является решением линейного дифференциального уравнения.
,(3.1)
где а, b – постоянные коэффициенты; – оператор дифференцирования.

Если в некоторый момент времени воздействие с системы снять и предоставить систему самой себе, то изменение переменной y во времени, ее свободное движение y_св(t), будет решением уравнения
. (3.2)
В соответствии с определением устойчивости САР по А.М. Ляпунову, САР будет устойчивой, если при t свободная составляющая y_св(t) будет стремиться к нулю. Решение уравнения (3.2) определяется корнями характеристического уравнения, которое получают из уравнения (3.1), приравнивая операторный полином а(р) нулю, т.е. уравнением
, (3.3)
в котором р означает уже не символ дифференцирования, а некоторое комплексное число.

Корни характеристического уравнения (3.3) могут быть вещественными, в том числе кратными, нулевыми, комплексными и мнимыми.

Если корни уравнения (3.3) вещественные и различные, то решение уравнения (3.2) будет иметь вид
, (3.4)
где n – порядок характеристического уравнения;

p_i – корни характеристического уравнения;

А_i – постоянные интегрирования.

При вещественных корнях характеристического уравнения р_i=_i уравнение (3.4) будет иметь вид
. (3.5)

Очевидно, что для устойчивой работы системы необходимо и достаточно, чтобы все слагаемые уравнения (3.5) с течением времени стремились к нулю. Это возможно, если все корни характеристического уравнения системы отрицательные. Наличие хотя бы одного положительного корня будет свидетельствовать о неустойчивости системы, т.к. тогда соответствующее слагаемое в уравнении (3.5) с течением времени будет возрастать.
Если среди корней характеристического уравнения системы будут вещественные кратные корни, то в уравнении (3.5) появятся составляющие вида
,
где B_i – постоянные интегрирования;

k – кратность корня.

Если кратный корень вещественный отрицательный, или комплексный с отрицательной вещественной частью, то множитель e^pit будет с течением времени убывать, а множитель в скобках неограниченно возрастать, т.е. появляется неопределенность типа . Но поскольку при отрицательных корнях множитель e^pit убывает быстрее множителя в скобках, то эта группа слагаемых при отрицательных корнях с течением времени будет стремиться к нулю.

Если среди корней характеристического уравнения имеются комплексные сопряженные вида p_i,i+1 = _ij_i, то в уравнении (3.5) появятся составляющие вида

,
где С_i, _i – новые постоянные.

В этом случае в системе возникают колебания выходной величины. Эти колебания будут затухающими только в том случае, если вещественная часть корней _i отрицательная. В противном случае система будет неустойчивой, т.к. амплитуда колебаний выходной величины с течением времени будет возрастать.

При наличии нулевых корней характеристического уравнения, в уравнении (3.5) появятся составляющие вида А_i и в системе установится произвольное отклонение выходной переменной от установившегося значения. Система будет нейтрально устойчивой.

Если среди корней характеристического уравнения будут мнимые p_i,i+1=j_i, то в уравнении (3.5) появятся составляющие вида A_isin(_it+_i) и выходная переменная системы будет совершать незатухающие гармонические колебания с постоянной амплитудой. Система будет находиться на границе устойчивости.

Корни характеристического уравнения наглядно можно представить на комплексной плоскости (рисунок 3.2), если в качестве ее осей принять корни  и  характеристического уравнения (плоскость корней р).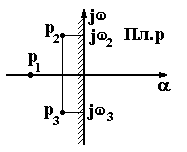


Рисунок 3.2
Рассматривая расположение корней на комплексной плоскости, можно отметить, что САР устойчива, если все корни характеристического уравнения замкнутой системы лежат в левой полуплоскости, левее мнимой оси, т.е. если все они вещественные отрицательные или комплексные с отрицательной вещественной частью. Мнимая ось в плоскости корней характеристического уравнения является границей устойчивости, которую принято отмечать штриховкой, направленной в сторону устойчивой зоны.

Таким образом, для определения устойчивости САР необходимо решить характеристическое уравнение замкнутой системы и проанализировать расположение ее корней на комплексной плоскости.

Решение характеристических уравнений высоких степеней вызывает определенные трудности. Поэтому желательно определять устойчивость системы не решая ее характеристического уравнения. Это можно сделать по значениям коэффициентов дифференциального уравнения или по виду частотных характеристик системы с помощью так называемых критериев устойчивости. Рассмотрим без доказательства некоторые из них.
3.3 Критерий устойчивости Гурвица
Критерий Гурвица формулируется следующим образом.

САР устойчива, если все коэффициенты однородного дифференциального уравнения замкнутой системы положительные, а определители Гурвица больше нуля.

Для рассмотрения критерия воспользуемся общей формой записи характеристического полинома замкнутой системы.
.
Из коэффициентов этого уравнения составляют главный определитель Гурвица _n, представляющий собой квадратную матрицу, содержащую n строк и n столбцов. Для этого по диагонали от левого верхнего до правого нижнего угла выписывают все коэффициенты по порядку от n-1 до а₀. Каждый столбец дополняют коэффициентами с последовательно возрастающими индексами сверху вниз. В случае отсутствия коэффициента на его месте пишут ноль. Определители Гурвица получают последовательным отчеркиванием на матрице строк и столбцов.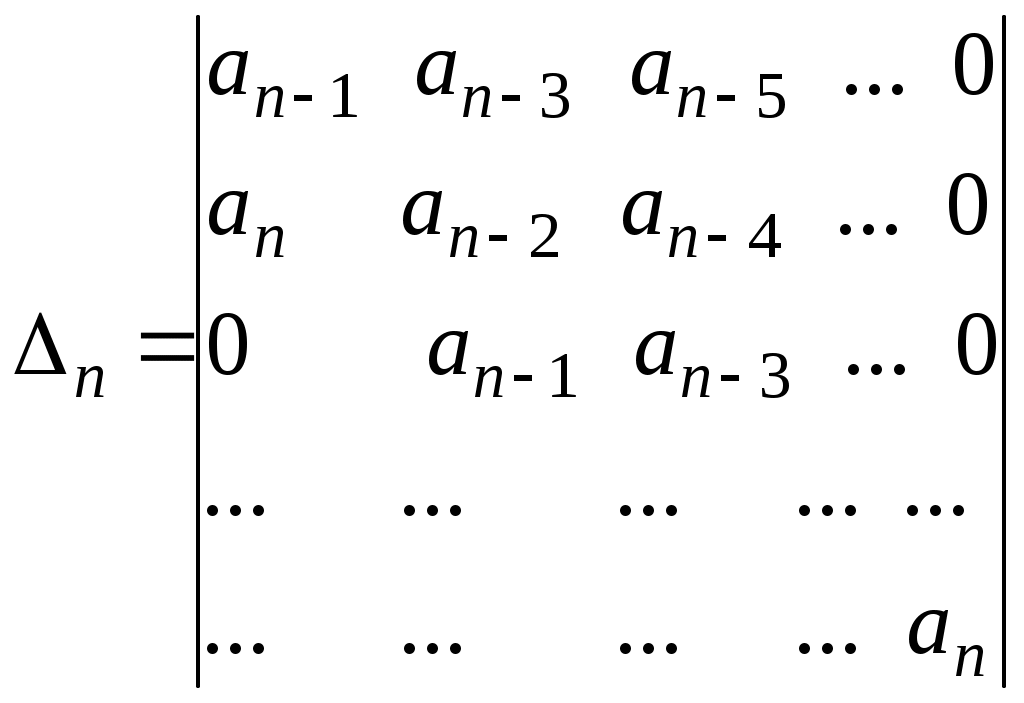
.
Условию устойчивости соответствуют следующие неравенства: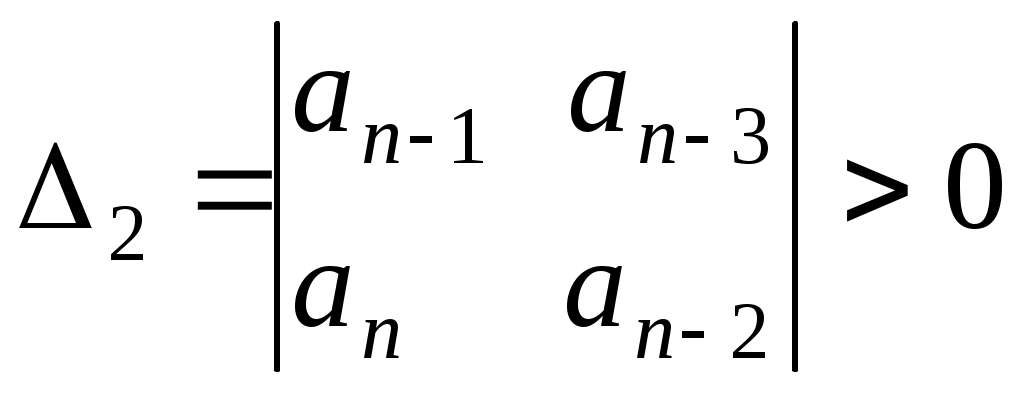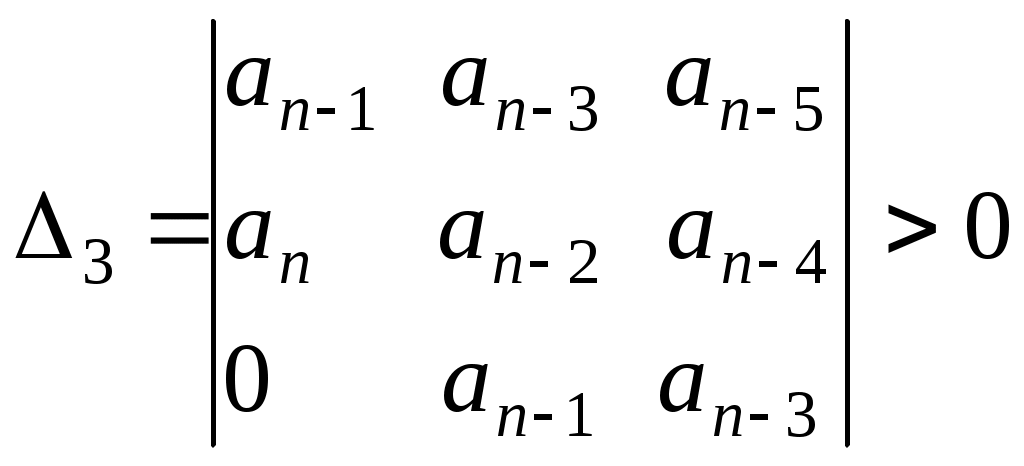
; ; .
Последний определитель включает всю матрицу, но он может быть выражен через предпоследний определитель Гурвица уравнением _n=a₀_n-10. В устойчивой системе предпоследний определитель тоже должен быть положительным. Поэтому положительность последнего определителя можно и не определять, если свободный член характеристического уравнения a₀0. В свою очередь, если главный определитель Гурвица _n=a₀_n-1 равен нулю, то система находится на границе устойчивости. Это возможно, если a₀ = 0 (один из корней характеристического уравнения равен нулю), или _n-1=0 (два корня характеристического уравнения мнимые). Это условие позволяет использовать критерий Гурвица для определения предельных (критических) значений отдельных параметров системы, при которых она будет находиться на границе устойчивости.
3.4 Критерий устойчивости Михайлова
Запишем выходной характеристический полином замкнутой САР следующим образом
.
Подставим в этот полином p=j, где  - угловая частота колебаний. Тогда получим характеристический комплекс, называемый вектором Михайлова.
,
где


называют соответственно вещественной и мнимой функциями Михайлова. Если изменять частоту  от нуля до бесконечности, то вектор D(j) будет изменяться по величине и направлению, описывая своим концом на комплексной плоскости кривую, называемую годографом Михайлова. Критерий Михайлова формулируется следующим образом.

САР устойчива, если годограф Михайлова при =0 начинается на вещественной положительной полуоси и с увеличением частоты проходит в положительном направлении против часовой стрелки последовательно n квадрантов, нигде не обращаясь в ноль, где n – порядок дифференциального уравнения или степень характеристического полинома. Любое отклонение от этого правила говорит о неустойчивости системы. Для системы, находящейся на границе устойчивости, годограф Михайлова проходит через ноль. На рисунке 3.3 показаны годографы Михайлова для устойчивых систем соответствующего порядка.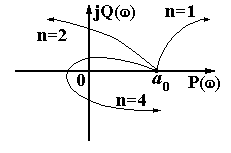

Рисунок 3.3

3.5 Критерий устойчивости Найквиста
Преимуществом критерия Найквиста является то, что он дает количественные оценки устойчивости и позволяет связать исследование устойчивости с последующим анализом качества и выбором оптимальных настроечных параметров регуляторов. Формулируется критерий Найквиста следующим образом.

САР, устойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если годограф АФХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывает на комплексной плоскости точку с координатами (-1, j0). Устойчивой системе соответствует годограф W₁(j) на рисунке 3.4. Если АФХ разомкнутой системы охватывает точку (1, j0), то замкнутая система будет неустойчивой. Неустойчивой системе соответствует годограф W₂(j) на рисунке 3.4. Если годограф АФХ разомкнутой системы проходит через точку (-1, j0), то система находится на границе устойчивости.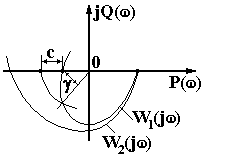

Рисунок 3.4

Для устойчивой системы по расположению годографа АФХ можно судить о так называемом запасе устойчивости. Чем дальше годограф АФХ разомкнутой системы проходит от точки (-1, j0), тем больше этот запас. Характеризуется он двумя численными величинами: запасом устойчивости по модулю С и запасом устойчивости по фазе  (рисунок 3.4).
Запас устойчивости по модулю определяется как расстояние от точки (1, j0) до точки пересечения годографа АФХ разомкнутой системы с отрицательной вещественной полуосью. Величина С находится в пределах от 0 до 1. Запас устойчивости по модулю показывает в каких пределах можно увеличивать модуль АФХ разомкнутой системы, чтобы замкнутая система оставалась устойчивой.
Запас устойчивости по фазе – это угол между отрицательной вещественной полуосью и лучом, проведенным из начала координат в точку пересечения годографа АФХ разомкнутой системы с окружностью единичного радиуса. Запас устойчивости по фазе показывает в каких пределах возможно увеличение запаздывания по фазе в разомкнутой системе, чтобы замкнутая система оставалась устойчивой.
3.6 Анализ устойчивости по логарифмическим частотным

характеристикам разомкнутой системы
Используя критерий Найквиста можно оценить устойчивость системы по ее логарифмическим частотным характеристикам. В соответствии с критерием Найквиста система будет находиться на границе устойчивости, если при значении ФЧХ системы () = модуль АЧХ системы А()=1. Поскольку lg1=0, то условию нахождения системы на границе устойчивости будут соответствовать значения ЛАЧХ разомкнутой системы L()=0 при ()=. Этот случай изображен на рисунке 3.5, а.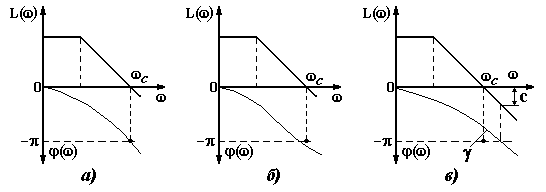

Рисунок 3.5

Если характеристика () принимает значение  при положительном значении характеристики L(), то система будет неустойчивой (рисунок 3.5, б). Если характеристика () принимает значение  при отрицательном значении характеристики L(), то система будет устойчивой (рисунок 3.5, в).

Тогда критерий Найквиста применительно к логарифмическим частотным характеристикам можно сформулировать следующим образом.

Замкнутая система будет устойчивой, если при достижении ЛФЧХ устойчивой разомкнутой системы значения –, логарифмическая амплитудно-частотная характеристика системы отрицательная. При этом запас устойчивости по амплитуде равен С, дБ., а по фазе , град., как это показано на рисунке 3.5,в. В заключение отметим, что изложенная формулировка критерия Найквиста справедлива только для так называемых систем с АФХ первого рода, у которых годограф АФХ разомкнутой системы пересекает отрицательную вещественную полуось комплексной плоскости только один раз.
3.7 Устойчивость систем с запаздыванием
САР, содержащую хотя бы одно запаздывающее звено, называют системой с запаздыванием. Структурная схема такой САР показана на рисунке 3.6.


Рисунок 3.6
Передаточная функция этой системы

имеет характеристическое уравнение
(3.6)
Это характеристическое уравнение из-за наличия множителя e^-p имеет бесконечное множество корней, т.к.

и по этой причине уравнение (3.6) можно рассматривать как уравнение «бесконечной степени».

Для того, чтобы линейная система с постоянным запаздыванием была устойчива, необходимо и достаточно, чтобы все корни уравнения (3.6) были левыми. Но нахождение всех корней уравнения (3.6) практически невозможно и поэтому для исследования устойчивости систем с запаздыванием используют критерии устойчивости, причем наиболее удобным здесь оказывается частотный критерий Найквиста. Формулировка критерия Найквиста остается без изменения.

АФХ разомкнутой системы с запаздыванием

. (3.7)
Из уравнения (3.7) следует, что наличие запаздывающего звена не меняет модуль А() АФХ разомкнутой системы, а вносит лишь дополнительный отрицательный фазовый сдвиг на величину . Имея график разомкнутой системы без запаздывания, легко перестроить его в график АФХ системы с запаздыванием. Для этого каждый вектор А(_i) АФХ системы без запаздывания следует повернуть на угол _i по часовой стрелке, как это показано на рисунке 3.7. При этом АФХ системы как бы «разбухает», в результате чего уменьшается запас устойчивости системы по модулю и по фазе. Изменяя время запаздывания  можно найти такое его значение, при котором замкнутая система будет находиться на границе устойчивости. В этом случае АФХ разомкнутой системы будет проходить через точку (-1, j0). Время запаздывания _кр и соответствующее ему значение частоты _кр, при которых АФХ разомкнутой системы проходит через точку (-1, j0) называют критическим. Определение критического времени запаздывания можно выполнить графическим способом (рисунок 3.8). Для этого для системы без запаздывания известным способом определяем запас устойчивости системы по фазе  (в радианах) и соответствующее ему значение частоты _кр. Тогда _кр=/_кр. По логарифмическим частотным характеристикам критическое время запаздывания определяется по уравнению _кр=/_с.

Таким образом критерий Найквиста для систем с запаздыванием можно сформулировать следующим образом.

Устойчивая замкнутая система без запаздывания будет устойчивой и при введении в нее запаздывающего звена, если время запаздывания меньше критического.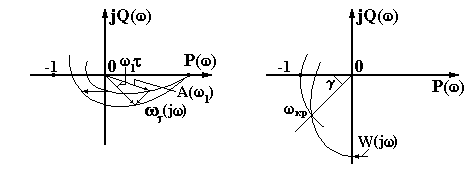


Рисунок 3.7 Рисунок 3.8
Для решения ряда практических задач, возникающих при анализе САР с запаздыванием, величину e^-p раскладывают в дробный ряд Падэ, оставляя в разложении только члены р со степенью равной единице. Тогда .

Пример. В системе с передаточной функцией в разомкнутом состоянии степень устойчивости =0,8, а степень колебательности m=1,2. Определить как изменятся эти параметры, если в системе появится запаздывание =2 с.

Находим передаточную функцию разомкнутой системы с запаздыванием.

Передаточная функция замкнутой системы

Характеристическое уравнение системы

Методом последовательных приближений найдены его корни.
р₁=1,34; р_2,3 = -0,63j0,64.
Система после появления запаздывания оказалась устойчивой, т.к. корни характеристического уравнения левые. Но степень устойчивости уменьшилась и стала равной 0,63. Степень колебания также уменьшилась и стала равной 0,98, что говорит о замедлении затухания переходного процесса, т.е. качество регулирования ухудшилось.
3.8. Построение областей устойчивости в плоскости параметров системы
3.8.1 Понятие о D-разбиении.

При исследовании систем на устойчивость часто представляет интерес не только факт устойчивости или неустойчивости системы, но и определение диапазона изменения какого-либо параметра системы, в пределах которого система остается устойчивой. Уравнение границы области устойчивости можно находить пользуясь любым критерием устойчивости, но наиболее общим является метод D-разбиения, предложенный Ю.И. Неймарном.

Рассмотрим характеристическое уравнение замкнутой системы n-го порядка.

. (3.8)
Каждый из коэффициентов уравнения (3.8) можно рассматривать как координатную ось n-мерного пространства, которое называют пространством коэффициентов. Если изменять коэффициенты a_i уравнения (3.8) его корни , в силу их зависимости от коэффициентов, будут перемещаться в плоскости корней и образовывать в ней области, имеющие к корней лежащих слева и n-k корней, лежащих справа от мнимой оси. Число к может изменяться от 0 до n. Эти области обозначают D(k). Разбиение пространства коэффициентов на области с одинаковым числом левых корней внутри данной области и выделение среди полученных областей области устойчивости, называют D-разбиением.

Наглядно суть D-разбиения можно представить для характеристического уравнения второй степени р²+а₁р+а₀=0. Пусть в этом уравнении коэффициенты а₁ и а₀ не определены и могут изменяться произвольным образом, образуя плоскость пространства коэффициентов а₀ а₁ (рис. 3.9). В этом пространстве линии ( а₁ 0 а₀) являются границей D-разбиения, отделяющей области D(0), D(1) и D(2). Очевидно, что область D(2) является областью устойчивости в пространстве коэффициентов а₀ а₁. Если не существует области D(2), то это значит, что система не может быть устойчивой.

Из рисунка 3.9 следует, что границу D-разбиения можно рассматривать как отражение мнимой оси плоскости корней р характеристического уравнения системы на пространство его коэффициентов, поскольку переход через линию D-разбиения в пространстве коэффициентов соответствует в плоскости корней переходу их через мнимую ось.

В соответствии с критерием Михайлова система будет находиться на границе устойчивости, если годограф Михайлова D(j) проходит через начало координат, чему соответствует условие
D(j) = P() + jQ() = 0,
где
P() = 0; Q() = 0 (3.9)
Решая уравнения (3.9) относительно исследуемых коэффициентов – параметров системы, например а₀ и а₁, считая остальные неизменными, получим выражения

a₀ = f₀(); a₁ = f₁() (3.10)
Изменяя в выражениях (3.10) частоту  от - до + можно построить кривую D-разбиения плоскости этих параметров и определить диапазон изменения этих параметров, соответствующий границе устойчивости.
3.8.2 Построение области устойчивости в плоскости одного комплексного параметра.

В том случае, когда необходимо исследовать влияние на устойчивость только одного параметра, например коэффициента передачи системы К, вместо этого параметра вводится комплексная величина, вещественная часть которой равна этому параметру, т.е. предполагается, что k=P()+jQ().

Для определения области устойчивости следует:

1) Разрешить характеристическое уравнение замкнутой системы относительно исследуемого параметра.

2) В полученном выражении заменить р на j и выделить его вещественную и мнимую части
P()=f₁(); Q()=f₂().
3) Изменяя частоту  от - до + вычислить значения P() и Q() и в плоскости P() и Q() построить D-разбиения.

4) Заштриховать кривую D-разбиения слева при движении от  = к =+. Область, в сторону которой направлена штриховка, будет иметь наибольшее число левых корней и будет претендовать на область устойчивости.

5. Выполнить проверку одной точки выделенной области на устойчивость и записать условие устойчивости (если оно существует). При этом следует рассматривать лишь действительные значения исследуемого параметра.

Пример. Дано характеристическое уравнение системы p²+2p+k=0. Определить пределы изменения к, при которых система будет устойчива.

Разрешаем исходноe уравнение относительно исследуемого параметра k=p²2p.

Вместо р подставляем j. Тогда k=²j2=P()+jQ(),

Где

P()=²; Q()=2.

В плоскости P()=Rek и Q()=Jmk строим кривую D-разбиения (рисунок 3.10).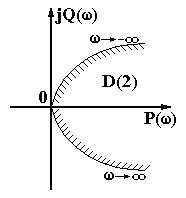

Рисунок 3.10

При частоте =0 Р()=0 и Q()=0;

при = 1 Р()=1 и Q()= 2 и т.д.

При  Р() и Q().

При   Р() и Q() +.

Кривую D-разбиения штрихуем слева при движении от = к =. Проверяем, является ли эта область областью устойчивости. Примем k=1. Тогда уравнение системы примет вид р²+2р+1=0. Его оба корня р_1,2=1 являются левыми. Следовательно, выделенная штриховкой на рисунке 3.10 область является областью устойчивости. Проверим граничную точку k=0. При k=0 уравнение системы примет вид р²+2р=0. Его корни р₁=0; р₂=2, т.е. один корень нулевой, а второй лежит слева от мнимой оси. Система находится на границе устойчивости. Следовательно, условию устойчивости рассматриваемой системы отвечают значения k  0.