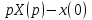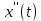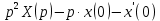01 Самостоятельная работа тема 1. Решение систем дифференциальных уравнений с помощью операционного исчисления
 Скачать 53.27 Kb. Скачать 53.27 Kb.
|
|
Самостоятельная работа по «Высшей математике» на тему: «Решение систем дифференциальных уравнений с помощью операционного исчисления» Выполнил студент: ____________________ Группа: SRQTA-1 Идея решения дифференциального уравнения операционным методом состоит в том, что от дифференциального уравнения относительно искомой функции-оригинала f ( t ) переходят к уравнению относительно другой функции F ( p ), называемой изображением f ( t ) . Полученное операционное уравнение обычно уже алгебраическое (значит более простое по сравнению с исходным). Решая его относительно изображения F ( p ) и переходя затем к соответствующему оригиналу, находят искомое решение данного дифференциального уравнения. Операционные исчисления. Функции оригинал Операционное исчисление- один из наиболее экономичных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами и пользуется большой популярностью у инженеров. Метод был предложен известным американским электротехником и физиком О. Хевисайдом (1892 г.). Он предложил формальные правила обращения с оператором d, dx и некоторыми функциями от этого оператора, используя которые решил ряд важнейших задач электродинамики. Однако операционное исчисление не получило в трудах О. Хевисайда математического обоснования (его математика возникала в физическом контексте, из которого ее нелегко было выделить, многие его результаты оставались недоказанными. Лишь в 20-е годы XX века метод получил обоснование в работах Бромвича и Карсона. Операционный метод решения дифференциальных уравнений можно сравнить с вычислением различных выражений при помощи логарифмов, когда, например, при умножении вычисления ведутся не над самими числами, а над их логарифмами, что приводит к замене умножения более простой операцией – сложением. Определение. Функцией- оригиналом - называют функцию f(t) действительного аргумента t, удовлетворяющую условиям: 1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е. f(t) 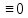 при t<0 при t<02) функция f(t) при t>0 возрастает не быстрее показательной функции, т.е. существуют такие постоянные M>0, S ≥0 , что |f(t)|≤M 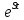 при t>0 при t>03) на любом конечном отрезке положительной полуоси Ot функция f(t)и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода. Простейшей функцией - оригиналом является единичная функция Хевисайда: 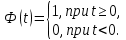 (1) (1)Если функция 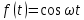 не удовлетворяет условию (1), то произведение не удовлетворяет условию (1), то произведение 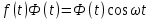 уже ему удовлетворяет, т.е. будет оригиналом. уже ему удовлетворяет, т.е. будет оригиналом.Преобразование Лапласа. Теоремы преобразования Лапласа. Преобразование Лапласа — интегральное преобразование, связывающее функцию F(S) комплексного переменного (изображение) с функцией f(x)  действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Виды преобразований Лапласа: 1. Прямое преобразование Лапласа. Преобразованием Лапласа функции действительной переменной f(t), называется функция F(S) комплексной переменной 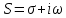 , такая что: , такая что: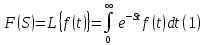 Правая часть этого выражения называется интегралом Лапласа. 2. Обратное преобразование Лапласа. Обратным преобразованием Лапласа функции комплексного переменного 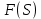 , называется функция , называется функция 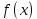 действительного переменного, такая что: действительного переменного, такая что: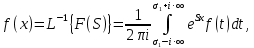 где 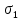 — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича. — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.3. Двустороннее преобразование Лапласа. Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции 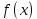 участвуют значения x < 0/ участвуют значения x < 0/Двустороннее преобразование Лапласа определяется следующим образом: 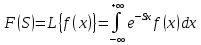 4. Дискретное преобразование Лапласа. Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций. Различают D-преобразование и Z-преобразование. D-преобразование Пусть 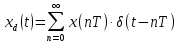 - решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени 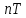 , где n- целое число, а , где n- целое число, а 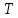 - период дискретизации. Тогда применяя преобразование Лапласа получим: - период дискретизации. Тогда применяя преобразование Лапласа получим: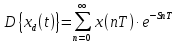 Z-преобразование Если применить следующую замену переменных: 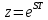 получим Z-преобразование: 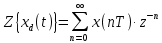 Преобразование Лапласа обладает следующими линейными свойствами: Преобразование суммы функций равно сумме преобразований этих функций: 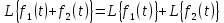 Постоянный множитель можно выносить за знак преобразования: 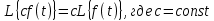 Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований: 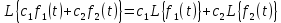 На конкретном примере рассмотрим преобразование Лапласа. Пример. Найти изображение функции 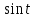 . .Решение: Используем формулу: 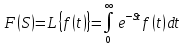 для функции 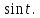 Тогда получим: 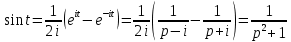 Перейдем к изучению некоторых основных свойств преобразования Лапласа: Теорема подобия. Для любого 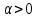 , , 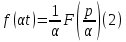 Доказательство: Подстановка 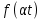 в формулу (1) и замена переменного в формулу (1) и замена переменного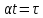 приводит к результату (2): приводит к результату (2):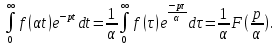 Теорема запаздывания. Для любого 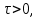 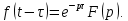 Теорема смещения. Для любого комплексного числа 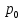 , ,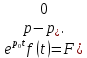 Доказательство свойства (3) элементарно путем подстановки его левой части в интеграл (1). Дифференцирование оригинала. Если функция 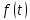 непрерывна при непрерывна при 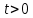 и и 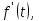 или в более общем случае или в более общем случае 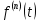 являются оригиналами, то являются оригиналами, то 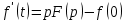 или 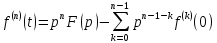 , ,где под 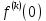 понимается предел справа в точке t=0 понимается предел справа в точке t=0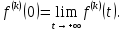 Дифференцирование изображения. Дифференцирование изображения сводится к умножению оригинала на (-t), то есть 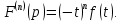 Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на p, то есть: 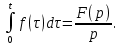 На основе рассмотренных теорем можно составить таблицу преобразования Лапласа. В таблице приведены наиболее часто встречающиеся преобразования. Здесь 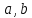 - различные постоянные. - различные постоянные.
Решение линейных систем обыкновенных дифференциальных уравнений Решение дифференциальных уравнений - основное приложение операционного метода, основанного на преобразовании Лапласа. Операционный метод включает следующие этапы: преобразование дифференциального уравнения с заданными начальными условиями по Лапласу; при этом образуется комплексное алгебраическое уравнение относительно изображения неизвестной функции; решение комплексного алгебраического уравнения; отыскание оригинала, искомого частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям. Операционный метод решения системы линейных дифференциальных уравнений включает следующие этапы: преобразование системы дифференциальных уравнений по Лапласу; при этом образуется система линейных алгебраических уравнений относительно изображений искомых функций; решение системы алгебраических уравнений, например, методом Крамера; отыскание оригиналов методами обратного преобразования Лапласа. Способ операционного исчисления применим к системе ДУ, когда задание сформулировано следующим образом: Найти частное решение однородной системы дифференциальных уравнений 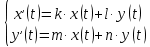 , соответствующее начальным условиям , соответствующее начальным условиям 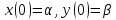 . .Как вариант, система может быть и неоднородной – с «довесками» в виде функций 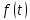 и и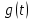 в правых частях: в правых частях: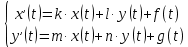 Но, и в том, и в другом случае нужно обратить внимание на два принципиальных момента условия: Речь идёт только о частном решении. В скобочках начальных условий 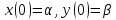 находятся строго нули, и ничто другое. находятся строго нули, и ничто другое.Общий ход и алгоритм будет очень похож на решение дифференциального уравнения операционным методом. Из справочных материалов потребуется в решении линейных систем обыкновенных дифференциальных уравнений таблица преобразований Лапласа. Примеры Пример №1 решения линейных систем обыкновенных дифференциальных уравнений С помощью операционного исчисления найти частное решение системы дифференциальных уравнений, соответствующее заданным начальным условиям. 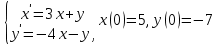 . .Решение: Начало такое: с помощью таблицы преобразования Лапласа перейдем от оригиналов к соответствующим изображениям. В задаче с системами ДУ данный переход обычно прост: Используя табличные формулы, учитывая начальное условие 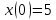 , получаем: , получаем: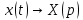 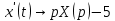 С переменную y проделываем тот же самый путь, меняя в таблице «x» на «y». Используя те же преобразования, учитывая начальное условие 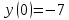 , находим: , находим: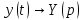 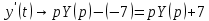 Подставим найденные изображения в исходное уравнение: 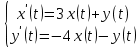 : :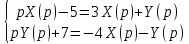 Теперь в левых частях уравнений нужно собрать все слагаемые, в которых присутствует 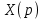 или или 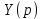 . В правые частиуравнений необходимо перенести все остальные слагаемые: . В правые частиуравнений необходимо перенести все остальные слагаемые: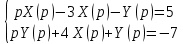 Далее в левой части каждого уравнения проводим вынесение за скобки: 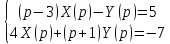 При этом на первых позициях следует разместить При этом на первых позициях следует разместить 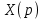 , а на вторых позициях , а на вторых позициях 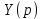 : :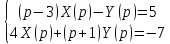 Полученную систему уравнений с двумя неизвестными 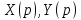 обычно решают по формулам Крамера. Вычислим главный определитель системы: обычно решают по формулам Крамера. Вычислим главный определитель системы: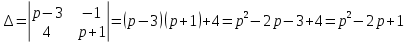 В результате расчёта определителя получен многочлен 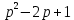 . .Далее идет важный технический прием. Данный многочлен лучше сразу же попытаться разложить на множители. В этих целях следовало бы попробовать решить квадратное уравнение 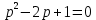 , но сразу можно заметить, что , но сразу можно заметить, что 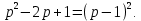 . .Таким образом, наш главный определитель системы: 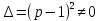 , значит система имеет единственное решение. , значит система имеет единственное решение.Дальнейшее решение проведем по методу Крамера: 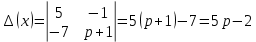 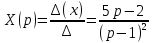 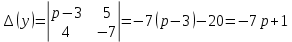 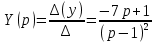 В итоге получаем операторное решение системы: 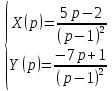 Преимуществом рассматриваемого задания является та особенность, что дроби обычно получаются несложными, и разбираться с ними значительно проще, нежели с дробями в задачах нахождения частного решения ДУ операционным методом. Далее решаем методом неопределенных коэффициентов, с помощью которого раскладываем каждую дробь на элементарные дроби: Разбираемся с первой дробью: 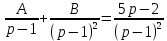 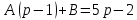 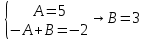 Таким образом: Таким образом: 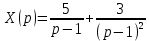 Вторую дробь разваливаем по аналогичной схеме, при этом корректнее использовать другие константы (неопределенные коэффициенты): 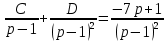 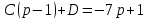 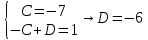 Таким образом: Таким образом: 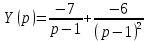 . .В результате операторное решение системы: 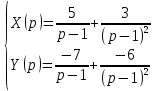 Также операторное решение можно записать в следующем виде: 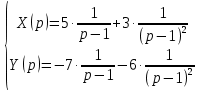 – так будет понятней завершающий этап – обратное преобразование Лапласа. – так будет понятней завершающий этап – обратное преобразование Лапласа.Перейдем от изображений к соответствующим оригиналам: 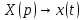 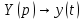 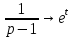 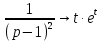 Подставим полученные изображения в операторное решение системы: 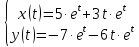 По правилам 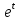 можно вынести за скобки, и тогда мы получим правильный ответ. можно вынести за скобки, и тогда мы получим правильный ответ. Ответ: 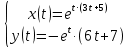 . . Пример №2 решения линейных систем обыкновенных дифференциальных уравнений Методом операционного исчисления найти частное решение системы дифференциальных уравнений 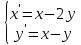 с заданными начальными условиями с заданными начальными условиями 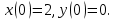 Решение: Перейдем от оригиналов к соответствующим изображениям: 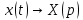 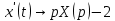 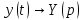 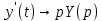 Подставим найденные изображения в исходную систему ДУ: 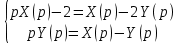 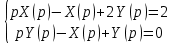 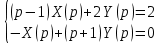 Систему решим по формулам Крамера: 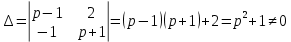 , значит, система имеет единственное решение. , значит, система имеет единственное решение.Полученный многочлен 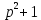 не раскладывается на множители. В этом случае многочлен можно оставить и в таком виде. не раскладывается на множители. В этом случае многочлен можно оставить и в таком виде. 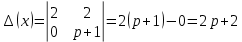 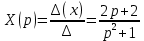 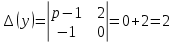 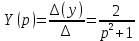 В результате операторное решение системы: 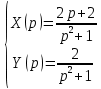 В данном случае метод неопределённых коэффициентов использовать не нужно. В целях применения табличных преобразований перепишем решение в следующем виде: 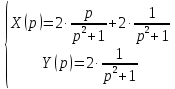 Перейдем от изображений к соответствующим оригиналам: 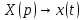 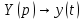 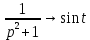 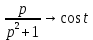 Подставим полученные изображения в операторное решение системы: 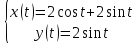 Ответ: частное решение: 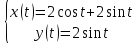 . . Здесь метод операционного исчисления действительно проще, чем «обычный» способ решения. |

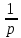
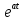
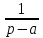
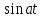
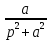
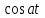
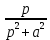
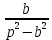
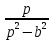
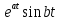
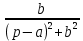
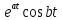
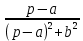
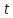
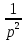
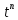
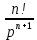
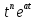
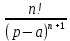
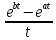
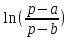
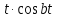
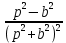
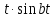
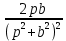
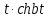
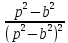
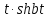
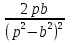
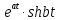
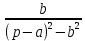
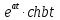
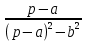
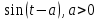
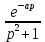
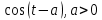
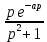
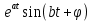
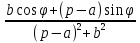
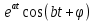
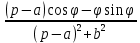
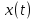
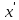 (t)
(t)