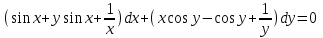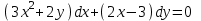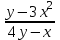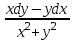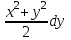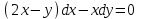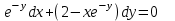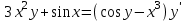Проект. зад 2 ДУ. 1 Линейные уравнения 1го порядка
 Скачать 88.75 Kb. Скачать 88.75 Kb.
|
|
1.3. Линейные уравнения 1-го порядка. Линейным уравнением 1-го порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид a0(x)y1+a1(x)y=b(x) или 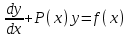 . .Если f(x) 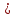 0, то уравнение называется линейным однородным. 0, то уравнение называется линейным однородным.Одним из методов решения линейного неоднородного уравнения является метод вариации произвольной постоянной, где общее решение состоит из двух слагаемых: первое является частным решением неоднородного уравнения, а второе–общее решение соответствующего однородного уравнения. Типовой пример: 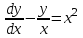 . .Решаем соответствующее однородное уравнение: 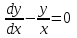 ; ; 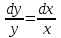 ; ln ; ln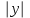 =ln =ln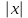 +ln c; y=cx. +ln c; y=cx.Считаем с функцией от x. Тогда y=c(x)x; 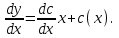 Подставляя в исходное уравнение, имеем: Подставляя в исходное уравнение, имеем: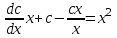 ; dc=xdx; c(x)= ; dc=xdx; c(x)=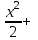 c1. Т.о. y= c1. Т.о. y=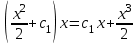 . .Вторым методом решения линейных уравнений является метод Бернулли. При котором решение ищут в виде y=u(x)v(x). И исходное уравнение сводится к решению двух уравнений с разделяющимися переменными. Типовой пример: x2y′–2xy=3. Разделяем обе части на x2 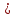 0: y′– 0: y′–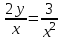 . .Общее решение ищем в виде y=u(x)v(x). Тогда y′=u′v+uv′ и подставляя в исходное уравнение получим: u′v+uv′– 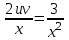 ; ; 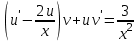 . .Приравняв выражение, стоящее в скобках, к нулю, получим систему ДУ: 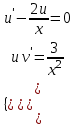 Решим первое уравнение системы: 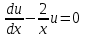 ; ; 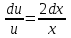 ; ln u=2ln x; ln u=ln x2; u=x2. ; ln u=2ln x; ln u=ln x2; u=x2.Подставим полученное и во второе уравнение системы: uv′= 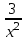 ; x2 ; x2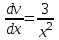 ; dv=3 ; dv=3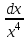 ; v=3 ; v=3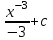 ; v= – ; v= –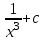 . .Т.о. общее решение имеет вид: y=x2 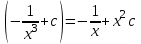 . .Примеры:
1.4. Уравнения в полных дифференциалах. Уравнением в полных дифференциалах называется уравнение P(x,y)dx+Q(x,y)dy=0, левая часть которого является полным дифференциалом некоторой функции u(x,y), т. е. du(x,y)= 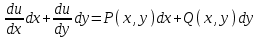 . .Для того, чтобы выражение Pdx+Qdy было полным дифференциалом, необходимо и достаточно, чтобы выполнялось условие Эйлера: 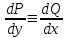 . .Типовой пример: (x+y+1)dx+(x–y2+3)dy=0. Проверяем условие Эйлера: 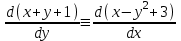 Т.о. 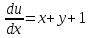 ; u= ; u=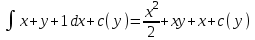 . .Для определения с(y) дифференцируем найденную функцию U по y и, т.к. 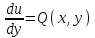 , получим , получим 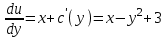 ; c′(y)=–y2+3; c(y)= – ; c′(y)=–y2+3; c(y)= –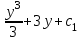 . .Т.о. u(x,y)= 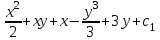 , или 3x2+6xy–6x–2y3+18y=c2, где c2=6c1 , или 3x2+6xy–6x–2y3+18y=c2, где c2=6c1Примеры:
|

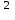
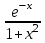
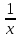
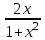
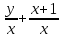
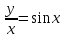
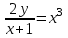
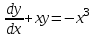
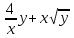
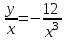
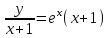
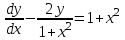
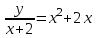
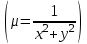
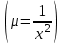
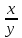 )dy=0
)dy=0