Этап урока, время
|
Действия учителя
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока (орг.момент)
|
- приветствие учащихся
- психологический настрой
- проверка готовности учащихся к уроку
|
- приветствуют учителя
- настраиваются на урок
|
Устный комментарий учителя
|
-
|
Начало урока (повторение, проверка дом.задания)
|
1 . Вопрос – ответ
Что называется числовым неравенством?
Какие неравенства называются строгими?
Какие неравенства называются нестрогими?
Какие неравенства называются двойными?
1.Игра «Найди пересечение интервалов» (по готовой таблице).
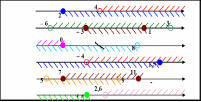
|
Отвечают на вопросы.
Находят пересечение интервалов.
Ответы: 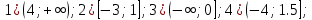
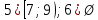
|
Похвала учителя
Пометки правильных ответов на полях.
Устный комментарий учителя
|
Презентация
|
Середина урока
|
Работа с классом.
На этом уроке учащимся предлагаются для решения более сложные системы неравенств. Кроме того, задания сформулированы таким образом, что требуется не только найти решение системы, но проверить выполнение каких-либо дополнительных условий.
Приложение 1
1) Решить неравенство:
а)
б) 
в) 
2) Найти целые решения системы неравенств.
а)  б) б) 
|
1) Один ученик выполняет у доски остальные в тетрадях.
а)

О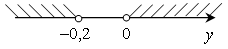 твет: . твет: .
б) 

О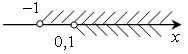 твет: (0,1; +∞). твет: (0,1; +∞).
в) Самостоятельно
О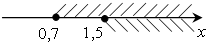 твет: [1,5; +∞). твет: [1,5; +∞).
2) Выполняют в тетрадях, один из учеников комментирует свое решение.
а) 
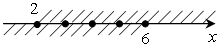 [2; 6]. [2; 6].
О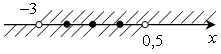 твет: Целыми решениями являются: 2; 3; 4; 5; 6. б) твет: Целыми решениями являются: 2; 3; 4; 5; 6. б)

(-3;0,5)
Ответ: Целыми решениями являются: –2; –1; 0.
|
устный комментарий учителя
|
|
Конец урока (закрепление)
|
Индивидуальная работа (Ф)(О)
Для того, чтобы проверить на сколько усвоил пройденный материал каждый ученик предлагается выполнить письменную самостоятельную работу.
Базовый уровень: Решите систему неравенств. 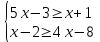
Средний уровень: Решите систему неравенств.
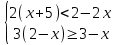
Продвинутый уровень: Найти целые решения системы неравенств.
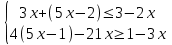
|
Выполняют задания.
Базовый уровень: Решают каждое неравенство исходной системы, получают:
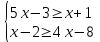 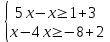 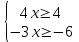 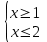
Изображают решение неравенств на одной координатной прямой:

Записывают ответ: [1; 2]
Средний уровень: Решают каждое неравенство исходной системы, получают:
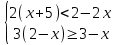 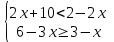 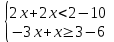 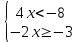 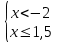
Изображают решение неравенств на одной координатной прямой:
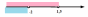 Записывают ответ: (-∞; -2) Записывают ответ: (-∞; -2)
Продвинутый уровень: Решают каждое неравенство исходной системы, получают:
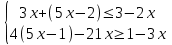 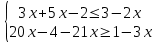 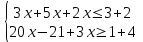 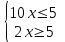 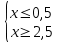
Изображают решение неравенств на одной координатной прямой:
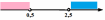 Записывают ответ: Записывают ответ: 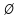
|
Оценивает по критериям.
Критерий оценивания:
-выполняет действия с неравенствами;
-изображает на координатной прямой пересечение и объединение числовых промежутков;
-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;
-находит решение системы неравенств.
|
|
Конец урока (подведение итогов, дом.задание)
|
Подведение итогов
Выставление баллов
Д/з Решите систему неравенств.
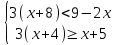
Найти целые решения системы неравенств.
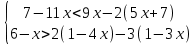
|
Учащиеся записывают д/з
|
устный комментарий учителя
|
|
 Скачать 261.87 Kb.
Скачать 261.87 Kb.