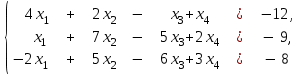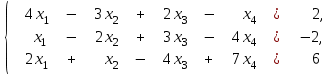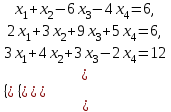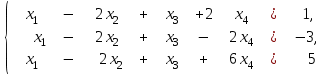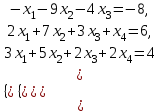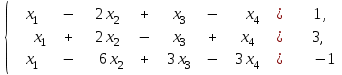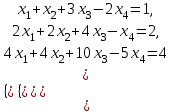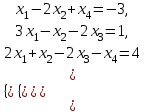Линейная алгебра и аналитическая геометрия. линалгебра. Решение системы следующими способами используя метод Гаусса, средства матричного исчисления, формулы Крамера

• Название: Решение системы следующими способами используя метод Гаусса, средства матричного исчисления, формулы Крамера
• Анкор: Линейная алгебра и аналитическая геометрия
• Дата: 02.03.2022
• Размер: 55.05 Kb.
• Имя файла: линалгебра.docx
• Тип: Решение; #380479

Задание

Дана система уравнений. Доказать ее совместность. Найти решение системы следующими способами: используя метод Гаусса, средства матричного исчисления, формулы Крамера.

№ вари-анта	Система линейных уравнений	№ вари-анта	Система линейных уравнений
1		6
2		7
3		8
4		9
5		10

Рекомендации по выполнению задания

Номер варианта задания можно определить по первой букве фамилии, используя таблицу «Выбор варианта решения». Решение расписывать как можно подробнее, описывать формулы, которыми пользуетесь во время решения – обязательно. Обязательно должно быть записано условие задания, ответ.
Выбор варианта задания

Буква	А, Ф, Э	Б, М, Х	В, Ю	Г, У, Я	Д, Ч, С	Е, Н, П	Ж, О, З	И, Ц	К, Т, Ш, Щ	Л, Р
№ вар.	1	2	3	4	5	6	7	8	9	10

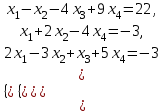Решение. 1. Докажем совместность системы, составим основную и расширенные матрицы: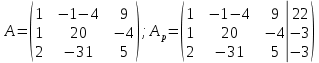

Найдем ранги матриц: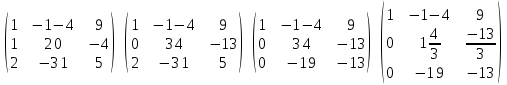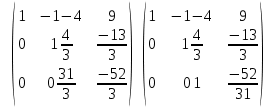





Ранг матрицы A равен 3.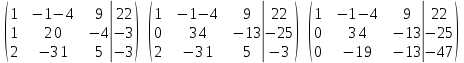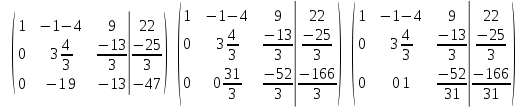





Ранг расширенной матрицы также равен 3, следовательно, система совместна.

2. Решим систему методом Гаусса: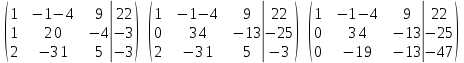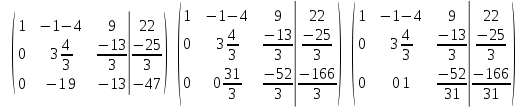





Последняя расширенная матрица эквивалентна системе: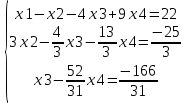



Базисные переменные x₁, x₂, x₃, свободные переменные x₄.

Выразив переменные x₁, x₂, x₃ через остальные, получим:

x1= 22 + 1 · x2 + 4 · x3 −9 · x4
x2= − 25 3 − 4 3 · x3 + 13 3 · x4

x3= − 166 31 + 52 31 · x4

где x₄− произвольное действительное число.

Подставив нижние выражения в верхние, получим решение.

x1= − 19 31 − 6 31 · x4
x2= − 37 31 + 65 31 · x4

x3= − 166 31 + 52 31 · x4

Далее невозможно решить методом матричного исчисления и формулой Крамера, так как в обоих случаях нужно находить определитель матрицы,а для этого матрица должна быть квадратной(число строк и столбцов должны совпадать).

Ответ :

x1= − 19 31 − 6 31 · x4
x2= − 37 31 + 65 31 · x4

x3= − 166 31 + 52 31 · x4 x4− произвольное действительное число