Метод эквивалентного генератора. МЭГ. Решение Сначала определим величину напряжения элемента схемы kUbd. Это напряжение равно UkUbd k(E2I2R2) 6(E2I2R2)
 Скачать 323 Kb.
|
|
Дано: R1=15 Ом; R2=20 Ом; R3=30 Ом; R4=5 Ом; R5=7 Ом; R6=25 Ом; Е2=7.5 В; J2=0.2 А; J3=0.5 А; k=6 Найти: ток I1 (методом эквивалентного генератора) Решение Сначала определим величину напряжения элемента схемы kUbd. Это напряжение равно U=kUbd = k(E2-I2*R2)= 6(E2-I2*R2) Укажем направления токов в цепи произвольным образом. 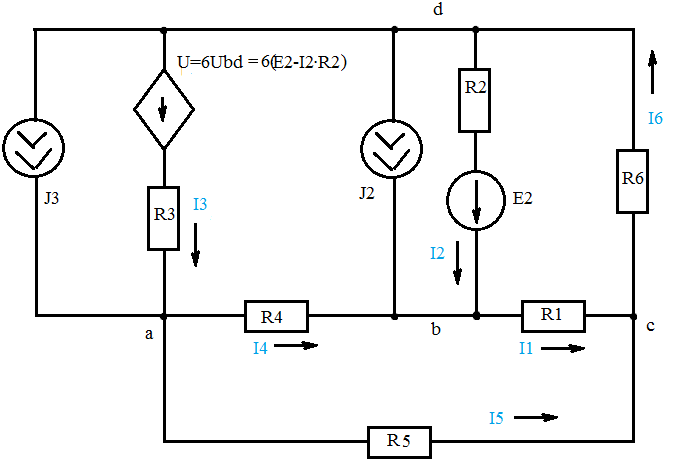 Для узлов a, b, c запишем три уравнения по первому закону Кирхгофа J3+I3-I4-I5=0 J2+I2+I4-I1=0 I1+I5-I6=0 По второму закону Кирхгофа для трех контуров R1-R5-R4-R1, R1-R2-R6-R1, R3-R6-R1-R4-R3 запишем еще три уравнения I1*R1+I4*R4-I5*R5=0 -I6*R6-I1*R1-I2*R2=-E2 -I3*R3-I6*R6-I1*R1-I4*R4= -6E2+6I2*R2 Получаем систему уравнений относительно шести токов J 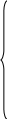 3+I3-I4-I5=0J2+I2+I4-I1=0 I1+I5-I6=0 I1*R1+I4*R4-I5*R5=0 -I6*R6-I1*R1-I2*R2=-E2 -I3*R3-I6*R6-I1*R1-I4*R4= -6E2+6I2*R2 Найдем ее решение 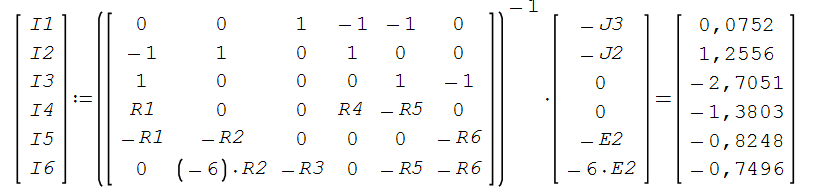 Получив ток I2=1,2556 A, находим напряжение U = 6(E2-I2*R2)=6*7.5-6*1.2556*20= -105.72 B Выполним замену в схеме элементы U и R3 на идеальный источник тока J3` Его значение равно J3` = U/R3=-105.72/30= - 3.524 A Схема будет выглядеть так: 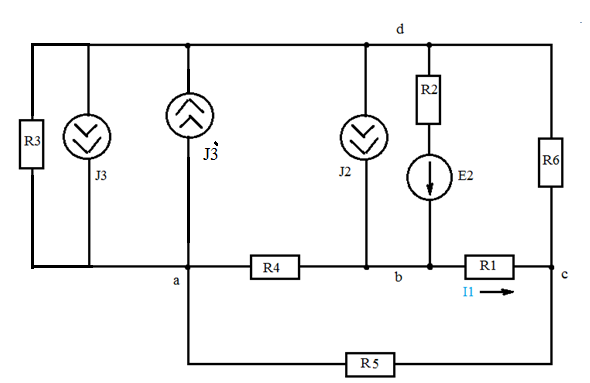 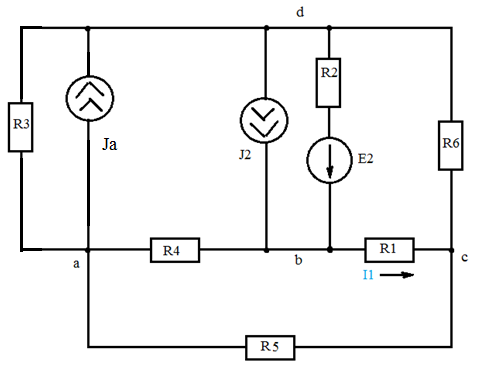 Два идеальных источника токов J3 и J3` заменим на эквивалентный источник тока, равный 3.524 - 0.5 =3.024 А Этот идеальный источник тока заменим на источник ЭДС Еa Ea=Ja*R3=3.024*30= 90.72 B 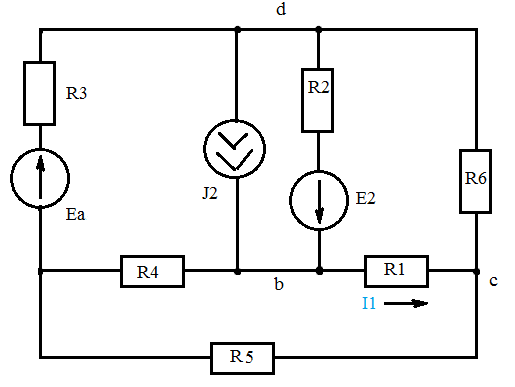 Аналогично проделаем замены элементов схемы J2, Е2, R2 J2`=E2/R2=0.375 A; Jb=J2+J2` =0.2+0,375=0.575 A Eb= J2`*R2=0.575*20 =11.5 B Теперь схема будет иметь вид: 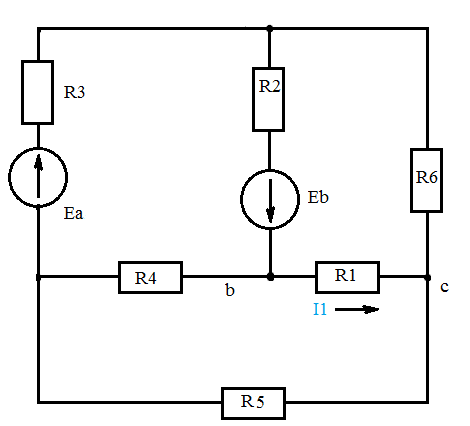 Применяем метод эквивалентного генератора. Разорвем ветвь с R1. 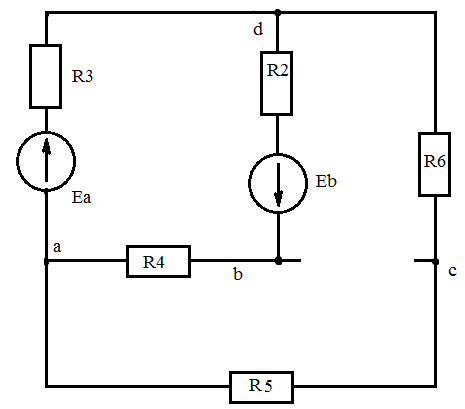 А) Найдем напряжение Ubc. Это напряжение будет напряжением генератора Еген. Пусть потенциал узла с равен 0 (φс=0). Для других узлов запишем равенства. Получим систему уравнений: φ  a(1/R5+1/R4+1/R3) - φd(1/R3)- φb(1/R4)=-Ea/R3φb(1/R2+1/R4)- φa(1/R4) - φd(1/R2)=Eb/R2 φd(1/R3+1/R2+1/R6)- φa(1/R3) - φb(1/R2)=Ea/R3 - Eb/R2 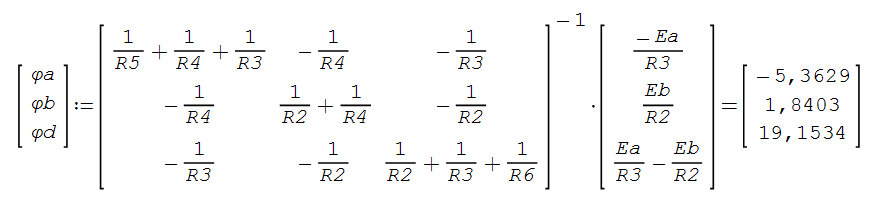 Таким образом, Еген=Ubc= φb – φc=1.8403 – 0 =1.8403 B Б) Найдем сопротивление генератора. Исключаем из схемы все источники ЭДС. 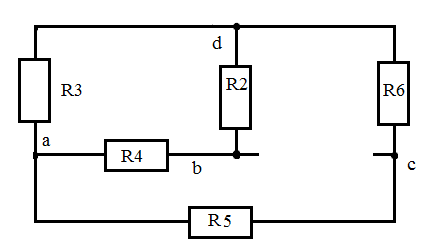 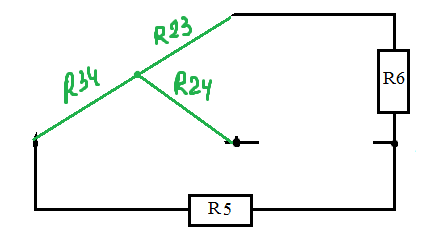 Заменим соединение сопротивлений «треугольник» на эквивалентные сопротивления R23, R24, R34. Последовательные сопротивления R23 и R6 заменим на Ra, аналогично R34 и R5 на Rb. Далее Ra и Rb заменим на Rab (они параллельны). Наконец, получаем общее сопротивление R. 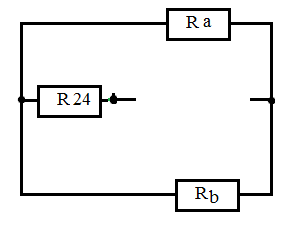 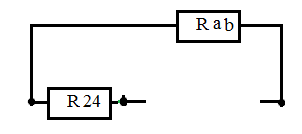 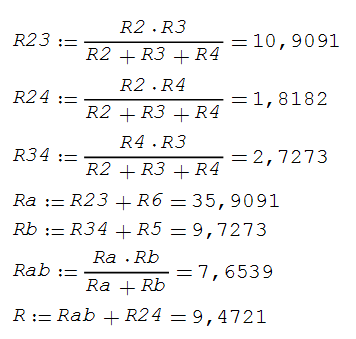 Итак, сопротивление генератора равно Rген = R = 9.4721 Ом Теперь восстанавливаем ранее разорванную ветвь и по закону Ома вычисляем ток I1. 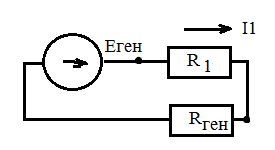 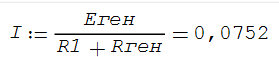 Ответ: I1=0.0752 A Дополнительная проверка расчетов. 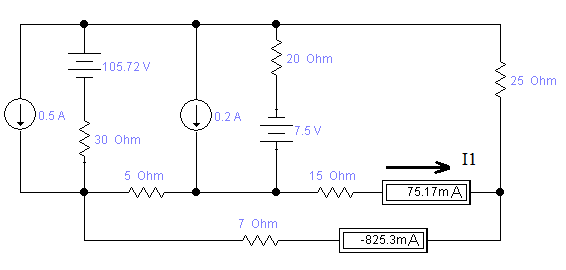 Показания амперметра A1 совпадают с расчетной величиной тока I1. |