задача 2. Решение. В приведенной электрической цепи четыре узла, шесть ветвей

• Название: Решение. В приведенной электрической цепи четыре узла, шесть ветвей
• Дата: 26.02.2023
• Размер: 121.65 Kb.
• Имя файла: задача 2.docx
• Тип: Решение; #955322

Параметры электрической схемы.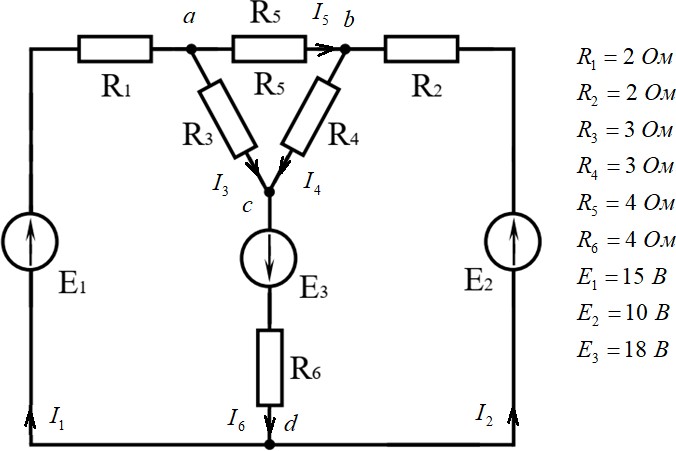


Решение.

1. 
   В приведенной электрической цепи четыре узла, шесть ветвей,
   

следовательно, для определения токов в ветвях методом законов Кирхгофа необходимо составить систему из шести уравнений для неизвестных токов.

I₁  I₃  I₅  0

I₂  I₄  I₅  0

I₃  I₄  I₆  0

I₁ R₁  I₃ R₃  I₆ R₆  E₁  E₃

I₃ R₃  I₄ R₄  I₅ R₆  0

I₂ R₂  I₄ R₄  I₆ R₆  E₂  E₃

для узла aдля узла bдляузлаc

для контура dacdдляконтураabca

дляконтураdcbc

Решив систему уравнений относительно токов в ветвях, можно определить все неизвестные токи.

2. 
   Метод узлового напряжения эффективен при расчете электрических цепей с двумя узлами и большим количеством параллельных ветвей или
   

более сложных схем, которые легко могут быть приведены к двухузловым.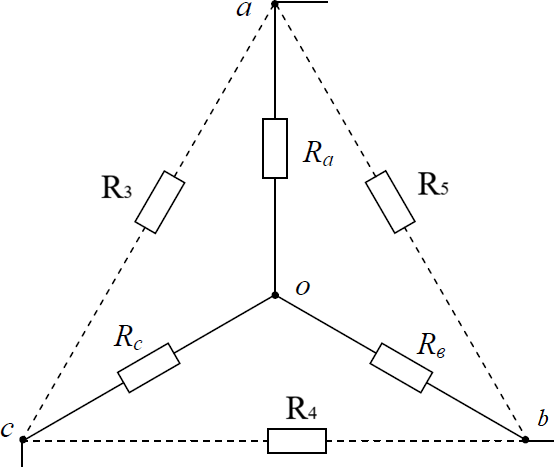

Заданная схема четырехузловая. Выделим треугольник авс пассивных элементов и преобразуем его в эквивалентную звезду.

_R ^R₃ ^R_{5 } 3 4

 1, 2 Ом

^a R R R 3  3  4

3 4 5

_R ^R₄ ^R_{5 } 4  3


 1, 2 Ом

^м R R R 3  3  4

3 4 5

_R ^R₃ ^R_{5 } 3 3


 0,9 Ом

^с R R R 3  3  4

3 4 5
В результате преобразований получена двухузловая схема.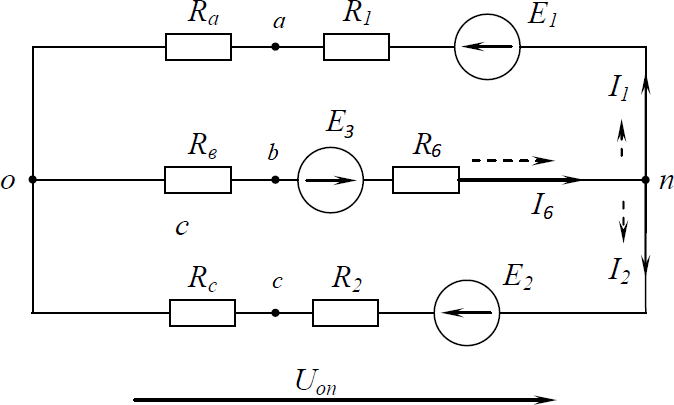




Рассчитываем проводимости ветвей схемы.

G₁  G₂  G₆ 

1


R₁  R_a

1

R₂  R_и

1

R₆  R<sub>с

</sub> 1

2 1, 2

_ 1

2 1, 2

_ 1

2  0,9

 0,3125 См
 0,3125 См
 0, 20408 См

Направление узлового напряжения указывается произвольно, положительный знак ответа подтверждает правильность выбора.

Отрицательный знак ответа указывает на то, что истинное направление – противоположно. Рассчитываем напряжение.

_{U } ^E₁^G₁ ^{ E}₂^G₂ ^{ E}₃^G_{6 } 15  0,3125 10  0,3125 18  0, 20408 _{ 4,992 B}

^on G G G 0,3125  0,3125  0, 20408

1 2 6
Токи в ветвях определяем по обобщённому закону Ома.

^{I1 }  ^{E1 Uon} ^{G1 } ^{15  4,992} ^{ 0,3125  3,127 A; I2 }  ^{E2 Uon} ^{G2 } ^{10  4,992}^{ 0,3125  1,565 A; I6 }  ^{E3  Uon}^{G6 } ^{18  4,992} ^{ 0,3125  4, 692 A.}

Выполняем проверку правильности расчета по первому закону

Кирхгофа. I₁  I₂  I₆ ; 3,127 1,565  4,962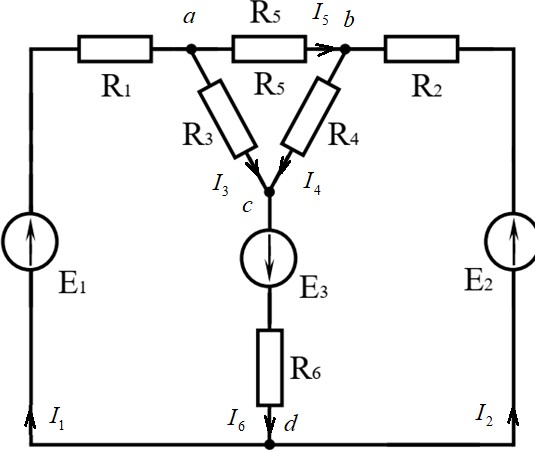

3. 
   Возвращаемся к исходной схеме. Истинные токи соответствуют выбранным.
   

Используя аторой закон Кирхгоффа определяем токи во всех ветвях схемы.

Для контура dacd

I₁ R₁  I₃ R₃  I₆ R₆  E₁  E₃

3
_I E₁  E₃  I₁ R₁  I₆ R₆

R<sub>3

</sub> 15 10  3,127  2  4, 692  4 _{ 2, 659 A}

3

Для контура dcbc

I₂ R₂  I₄ R₄  I₆ R₆  E₂  E₃

4
_I E₂  E₃  I₂ R₂  I₆ R₆

R<sub>4

</sub> 18 10 1,565 2  4, 692  4 _{ 2, 034 A}

3

Для контура abca

I₃ R₃  I₄ R₄  I₅ R₆  0

5
_I I₃ R₃  I₄ R₄

R<sub>5

</sub> 2, 659  3  2, 034  3 _{ 0, 469 A}

4

4. 
   Проверка правильности расчета задачи осуществляется по уравнению баланса мощностей. Уравнение баланса мощностей для рассматриваемой схемы.
   

EI EI EI I² R I²² R I² R I² R I² R I² R

1 1 2 2 3 6 1 1 2 2 3 3 4 4 5 5 6 6
Подставляем значения, решаем уравнение.

15  3,127 10 1,565 18  4, 692 

 3,127²  2 1,565²  2  2, 659²  3  2, 034²  3  0, 469²  4  4, 692²  4

147 Вт  147 Вт